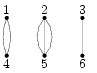Темы
    Информатика(2656 задач)
---> 97 задач <---
Источники --> Личные олимпиады --> Всероссийская олимпиада школьников --> Заключительный этап
    2004(6 задач)
    2005(6 задач)
    2006(6 задач)
    2007(6 задач)
    2008(6 задач)
    2009(6 задач)
    2010(6 задач)
    2011(8 задач)
    2012(8 задач)
    2013(8 задач)
    2014(7 задач)
    2015(8 задач)
    2016(8 задач)
    2017(8 задач)
Страница: << 2 3 4 5 6 7 8 >> Отображать по:
#1049
Горнолыжные соревнования
  
ограничение по времени на тест
0.5 second;
ограничение по памяти на тест
64 megabytes

Горнолыжник, готовясь к соревнованиям, нарисовал на бумаге схему горнолыжной трассы для выбора оптимального маршрута спуска. На схеме расположенные на трассе ворота представлены горизонтальными отрезками. Никакая пара ворот не имеет общих точек.

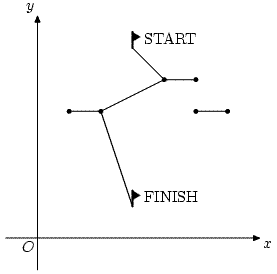
Маршрут должен представлять собой ломаную, начинающуюся в точке старта на вершине горы и заканчивающуюся в точке финиша у ее подножия. Маршрут выбирается таким образом, что y-координата каждой следующей вершины ломаной оказывается строго меньше y-координаты предыдущей вершины. Один из возможных маршрутов представлен на рисунке.

За каждые ворота, через которые не проходит маршрут, лыжнику начисляются штрафные очки. Общий штраф за спуск по маршруту вычисляется как сумма длины маршрута и штрафных очков за непройденные ворота.

Требуется написать программу, которая определяет, какой минимальный общий штраф горнолыжник может получить при прохождении трассы.

Входные данные

В первой строке входного файла задано число N - количество ворот на трассе (0 ≤ N ≤ 500), в следующих двух строках заданы Sx, Sy, Fx, Fy - координаты точек старта и финиша соответственно. В каждой из следующих N строк записаны четыре числа ai, bi, yi, ci - x-координаты левого и правого концов ворот, y-координата ворот и штраф за непрохождение данных ворот (ai < bi, Fy < yi < Sy, ci - целое число, 0 ≤ ci ≤ 10000). Все координаты - целые числа, не превосходящие по модулю 10000.

Выходные данные

В выходной файл выведите наименьший возможный общий штраф за прохождение трассы с точностью не менее 4 знаков после десятичной точки.

Система оценки

Потестовая.

Примеры
Входные данные
4
3 6
3 1
5 7 4 1
4 5 5 10
1 2 4 5
2 5 2 0
Выходные данные
7.8126
#1053
Pinball
  

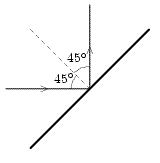
Поле в Pinball представляет собой прямоугольник без стенок, состоящий из n x m квадратных клеток, (n клеток по вертикали, m клеток по горизонтали). Клетки по вертикали нумеруются сверху вниз, по горизонтали - слева направо. В каждой клетке можно установить одну отражающую пластинку в одном из двух положений: в положении 1 - от левого верхнего угла к правому нижнему или в положении 2 - от левого нижнего к правому верхнему. Летящий шарик при столкновении с пластинкой изменяет свою траекторию, при этом угол падения шарика всегда равен углу отражения и составляет 45° (см. рисунок).

На границе прямоугольника заданы две точки A и B, являющиеся серединами сторон некоторых клеток поля. Пластинки расставляются таким образом, чтобы шарик, запущенный из точки A, попал в точку B. При этом шарик начинает движение внутрь поля перпендикулярно стороне клетки, на которой находится точка A.

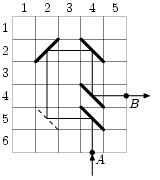Изначально на поле были расставлены k пластинок таким образом, чтобы шарик попал из точки A в точку B. После этого одну из пластинок удалили. Необходимо определить, куда и как можно поставить удаленную пластинку, чтобы шарик, выпущенный из точки A, попал в точку B. При этом требуется, чтобы длина пути шарика была минимальной. Пластинку нужно поставить на некоторую свободную клетку даже в том случае, если шарик попадает в точку B и без нее.

Требуется написать программу, устанавливающую пластинку таким образом, чтобы шарик попадал из точки A в точку B и длина его пути была минимальна.

Входные данные

Первая строка входного файла содержит три числа: n, m (1 ≤ n, m ≤ 1000) и k, где k - общее количество пластинок, которые были исходно расставлены.

Во второй строке указываются номера клетки по вертикали и по горизонтали, на границе которой лежит точка A, и номер стороны,на которой она находится. Стороны клетки пронумерованы целыми числами от 1 до 4, при этом верхней стороне присвоен номер 1, далее по часовой стрелке нумеруются остальные стороны.

Третья строка содержит описание точки B в том же формате.

 

 

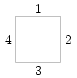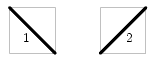Номера сторон клеток

Возможные положения пластинок

Следующие k-1 строк описывают пластинки, оставшиеся на поле. В каждой строке записаны по три числа: первое - номер клетки по вертикали, второе - номер клетки по горизонтали, третье - положение пластинки в клетке (число 1 или 2).

Выходные данные

Выходной файл должен содержать три числа: номера клетки, в которую следует поставить пластинку, по вертикали и горизонтали и ее положение. Если решений несколько, выведите любое.



Подзадача 1.

\(1 \leq n, m \leq 300\). Решение оценивается в \(50\) баллов.


Подзадача 2.

Дополнительные ограничения отсутствуют. Решение оценивается в \(50\) баллов.

#1054
Великолепный Гоша
  
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
64 megabytes
 

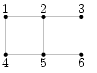
Телефонист Гоша получил задание соединить дома оптоволоконным кабелем по заданной схеме. На схеме указаны дома и их соединения между собой. При этом, согласно схеме может требоваться соединить два дома несколькими кабелями. Когда Гоша приехал на работу, он обнаружил, что схему оставил дома. Однако, у него оказались записи, фиксирующие, сколько кабелей должно быть подведено к каждому из домов. Он попытался восстановить схему, соединяя дома с использованием только имеющихся записей. По окончании работ оказалось, что получившаяся сеть схеме не соответствует. На рис. 1 показаны пример схемы и сети, реализованной Гошей.


 

 


 

          Схема

 

          Сеть Гоши

Рис. 1

На следующий день Гоша стал исправлять свою работу, глядя на верную схему. По техническим причинам он вынужден ограничиться последовательным выполнением операций только одного типа. В результате одной такой операции удаляются два кабеля, соединяющих некоторые две пары различных домов (см. рис. 2а), и эти же четыре дома соединяются либо как показано на рис. 2б, либо так, как на рис. 2в. Заметим, что после любой из таких операций количество кабелей, подведенных к каждому из домов, не меняется.



 





 

 

 

 

 

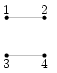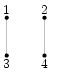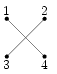а)


б)


в)

Рис. 2

Требуется написать программу, которая определяет, сможет ли Гоша за один рабочий день перестроить сеть согласно схеме, если за один день он выполняет не более 48000 операций. Если такая перестройка возможна, то программа должна выдать соответствующую последовательность операций.

Входные данные

В первой строке входного файла задано число N (4 ≤ N ≤ 1000) - количество домов на схеме. Во второй строке записано число M (2 ≤ M ≤ 20000) - количество кабелей в схеме. В следующих M строках расположены пары номеров домов, соединенных кабелями на схеме. Дома имеют номера от 1 до N. Затем в M строках указаны пары номеров домов, которые Гоша соединил кабелями.

Выходные данные

Если перестроить сеть согласно схеме невозможно, или для перестройки сети требуется более 48000 операций, то выходной файл должен содержать только число '-1'. В противном случае выходной файл должен содержать описание последовательности операций, по одной операции в строке.

Каждая операция описывается начальным и конечным положением кабелей. Сначала четырьмя целыми числами V1, V2, V3, V4 записывается исходное положение кабелей, при этом один из кабелей соединяет дома с номерами V1, V2, а другой --- V3, V4. Затем в таком же формате описывается конечное положение.

Примеры
Входные данные
5
2
1 2
3 4
1 3
2 4
Выходные данные
1 3 4 2 1 2 4 3
#1055
Красная шапочка
  

В непроходимом лесу имеется N полянок и M тропинок между ними. Каждая тропинка соединяет две различные полянки. Две полянки могут быть соединены несколькими тропинками.

На двух разных полянках живут Красная Шапочка и ее бабушка. Домик Красной Шапочки находится на полянке с номером 1, а домик бабушки - на полянке с номером N. Красная Шапочка хорошо ориентируется в лесу и знает, какое минимальное время ей потребуется для прохождения каждой тропинки. Когда Красная Шапочка идет по лесу, она переходит с тропинки на тропинку только на полянках. На каждой полянке есть укрытие, в котором Красная Шапочка может спрятаться на некоторое время.

В этом же лесу живет Волк. Время, за которое Волк пробегает какую-либо тропинку, может отличаться от времени, за которое по ней проходит Красная Шапочка. Кроме того, если Волк пробегает по одной и той же тропинке несколько раз, то каждый раз он может тратить на это разное время.

С края полянки, где живет Красная Шапочка, Волк увидел, что она собирается нести пирожки бабушке и побежал по тропинкам привычного ему пути от дома Красной Шапочки к дому бабушки. Волк начинает бежать от домика Красной Шапочки в тот момент, когда она решила выйти из дома, его путь заканчивается как только он окажется на полянке с домиком бабушки. Ни на одной полянке Волк не задерживается.

Чтобы застать бабушку в целости и сохранности, Красной Шапочке необходимо обогнать Волка. При этом ей нельзя оказаться с Волком на одной тропинке, даже если Волк уже покидает ее, а она только появляется на ней, или наоборот. Чтобы избежать встречи с Волком на полянке, Красная Шапочка использует имеющееся там укрытие. Красной Шапочке нельзя появляться на полянке одновременно с Волком или покидать укрытие на полянке в тот момент, когда на ней появляется Волк. При необходимости Красная Шапочка может идти по тропинке дольше минимально возможного времени, а также выйти из дома позже, чем она исходно решила.

Необходимо написать программу, которая поможет Красной Шапочке добраться к бабушке раньше Волка, если известна последовательность тропинок, по которым побежал Волк.

Входные данные

Первая строка входного файла содержит числа N, M и K (2 ≤ N ≤ 2000, 1 ≤ M ≤ 100000, 1 ≤ K ≤ 100000). Следующие M строк содержат по три числа: Bi, Ei - номера полянок, которые соединяет i-я тропинка, и Ti - минимальное время, за которое Красная Шапочка может по ней пройти (1 ≤ Ti ≤ 10000). В следующих K строках находится последовательное описание пути Волка, по два числа в строке: Pi - номер тропинки, по которой он побежит, и Vi - время, которое он на это затратит (1 ≤ Vi ≤ 10000). Путь волка всегда начинается на полянке 1 и заканчивается на полянке N. Все числа во входном файле целые и в пределах одной строки разделены пробелами.

Выходные данные

В том случае, если Красная Шапочка не может добраться до домика бабушки быстрее Волка, выходной файл должен содержать слово 'NO'.

Если Красная Шапочка сможет добраться до домика бабушки быстрее волка, в первой строке выходного файла должно быть слово 'YES'. Во второй строке в этом случае должно содержаться число тропинок в пути Красной Шапочки. В третью строку следует вывести номера тропинок в том порядке, в котором Красная Шапочка должна по ним пройти. Числа должны быть разделены пробелами.

Информацию о времени прохождения по тропинкам и остановках на полянках в выходной файл выводить не нужно.



Подзадача 1.

\(2 \leq N \leq 200\) Решение оценивается в \(30\) баллов.

Подзадача 2.

\(NK \leq 6 \cdot 10^6\) Решение оценивается в \(40\) баллов.

Подзадача 3.

Дополнительные ограничения отсутствуют. Решение оценивается в \(30\) баллов.

Примеры
Входные данные
3 2 3
1 2 13
1 3 9
1 5
1 5
2 5
Выходные данные
YES
1 2
#1216
Школа танцев
  

В школу бальных танцев профессора Падеграса записались n учеников — мальчиков и девочек. Профессор построил их в один ряд, и хочет отобрать из них для первого занятия группу стоящих подряд учеников, в которой количество мальчиков и девочек одинаково. Сколько вариантов выбора есть у профессора?

Входные данные

В первой строке задано число n (1 ≤ n ≤ 106). Во второй строке задается описание построенного ряда из мальчиков и девочек — строка из n символов a и b (символ a соответствует девочке, а символ b — мальчику).

Выходные данные

В единственной строке должно содержаться единственное число — количество вариантов выбора требуемой группы.

Система оценки

Тесты в этой задаче разбиты на группы. Баллы начисляются только за группу целиком в том случае, когда пройдены все тесты группы, а также все тесты предыдущих групп.

  1. Тест 1. Тест из условия, оценивается в 0 баллов.
  2. Тесты 2–8. \(N \le 101\), оцениваются в 30 баллов.
  3. Тесты 9–14. \(N \le 6\,000\), оцениваются в 30 баллов.
  4. Тесты 15–20. Дополнительных ограничений нет, оцениваются в 40 баллов.

Примеры
Входные данные
8
aabbaabb
Выходные данные
10
Страница: << 2 3 4 5 6 7 8 >> Отображать по:
Выбрано
:
Отменить
|
Добавить в контест