Алгоритмы(1657 задач)
Структуры данных(279 задач)
Интерактивные задачи(17 задач)
Другое(54 задач)
Для подготовки к чемпионату мира по футболу 2018 года создается школа олимпийского резерва. В нее нужно зачислить \(M\) юношей 1994−1996 годов рождения. По результатам тестирования каждому из \(N\) претендентов был выставлен определенный балл, характеризующий его мастерство. Все претенденты набрали различные баллы. В составе школы олимпийского резерва хотелось бы иметь \(A\) учащихся 1994 г.р., \(B\) – 1995 г.р. и \(C\) – 1996 г.р. (\(A + B + C = M\)). При этом минимальный балл зачисленного юноши 1994 г.р. должен быть больше, чем минимальный балл зачисленного 1995 г.р., а минимальный балл зачисленного 1995 г.р. должен быть больше, чем минимальный балл зачисленного 1996 г.р. Все претенденты, набравшие балл больше минимального балла для юношей своего года рождения, также должны быть зачислены.
В базе данных для каждого претендента записаны год его рождения и тестовый балл. Требуется определить, сколько нужно зачислить юношей каждого года рождения \(M_{94}\), \(M_{95}\) и \(M_{96}\) (\(M_{94} + M_{95} + M_{96} = M\)), чтобы значение величины \(F = |M_{94} − A| + |M_{95} − B| + |M_{96} − C|\) было минимально, все правила, касающиеся минимальных баллов зачисленных, были соблюдены, и должен быть зачислен хотя бы один юноша каждого требуемого года рождения.
В первой строке входного файла находится число \(K\) – количество наборов входных данных. Далее следуют описания каждого из наборов. В начале каждого набора расположены три натуральных числа \(A\), \(B\), \(C\). Во второй строке описания находится число \(N\) – количество претендентов (гарантируется, что \(N \geq A + B + C\)). В каждой из следующих \(N\) строк набора содержатся два натуральных числа – год рождения (число 1994, 1995 или 1996 соответственно) и тестовый балл очередного претендента.
Ответ на каждый тестовый набор выводится в отдельной строке. Если хотя бы одно из требований выполнить невозможно, то в качестве ответа следует вывести только число −1. В противном случае соответствующая строка сначала должна содержать минимальное значение величины \(F\), а затем три числа \(M_{94}\), \(M_{95}\) и \(M_{96}\), на которых это минимальное значение достигается, удовлетворяющие всем требованиям отбора. Если искомых вариантов несколько, то разрешается выводить любой из них.
В первом примере на первом наборе ответ не существует, потому что нельзя пригласить хотя бы одного юношу 1995 г.р. Во втором наборе ответ существует и единственный, в третьем – нельзя выполнить правило относительно минимальных баллов.
Во втором примере правильным является также ответ 2 2 2 2.
Данная задача содержит три подзадачи. Для оценки каждой подзадачи используется своя группа тестов. Баллы за подзадачу начисляются только в том случае, если все тесты из этой группы пройдены.
\(K = 1\); \(N \leq 100\); каждый претендент характеризуется своим баллом от 1 до \(N\).
Сумма значений \(N\) по всем тестовым наборам не превосходит 10 000, каждый претендент характеризуется своим баллом от 1 до \(10^9\).
Сумма значений \(N\) по всем тестовым наборам не превосходит 100 000, каждый претендент характеризуется своим баллом от 1 до \(N\).
Сумма значений \(N\) по всем тестовым наборам не превосходит 300 000, каждый претендент характеризуется своим баллом в диапазоне от 1 до \(10^9\).
3 1 1 1 4 1994 3 1994 4 1996 1 1996 2 1 1 1 3 1995 2 1994 3 1996 1 1 1 1 3 1994 1 1995 2 1996 3
-1 0 1 1 1 -1
1 2 3 1 7 1996 2 1994 7 1994 4 1996 1 1995 3 1994 5 1995 6
2 3 2 1
К 50-летию первого пилотируемого полета в космос решено создать новый тип космического корабля многоразового использования “Восторг”. Прямоугольная часть его корпуса (далее прямоугольник) должна быть облицована квадратными термозащитными плитками разных цветов одного и того же размера. Прямоугольник состоит из \(r\) рядов по \(c\) плиток в каждом. Плитки должны образовывать заданный рисунок.
Облицовка космического корабля отдельными плитками очень трудоемка, поэтому для выкладывания заданного рисунка используются одинаковые прямоугольные панели, состоящие из плиток. Панели крепятся на корпусе одна за другой, заполняя ряд за рядом сверху вниз. Каждый ряд панелей может быть сдвинут относительно предыдущего на одно и то же число плиток. При этом панели могут выходить за пределы прямоугольника. Панели должны быть одинаково ориентированы, то есть при параллельном переносе одной панели на место другой цвета образующих эти панели плиток должны совпадать.
Главный конструктор хочет выбрать такой размер панели \(a\times b\) и сдвиг \(s\), чтобы этими панелями можно было выложить заданный рисунок, и площадь панели была минимальна.
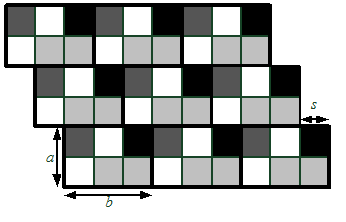
Требуется написать программу, которая по заданному расположению плиток в прямоугольнике рассчитывает размеры минимальной по площади панели, которую можно использовать при его облицовке, а также величину сдвига вправо (\(0 \leq s < b\)) каждого следующего ряда относительно предыдущего.
Первая строка входного файла содержит два целых числа: \(r\) и \(c\) – размеры прямоугольника в плитках. В последующих \(r\) строках указаны цвета плиток фрагмента. Каждый из \(k \leq 26\) цветов обозначен одной из первых \(k\) прописных букв латинского алфавита. Гарантируется, что для этого прямоугольника можно подобрать панель размера \(a\times b\), такую, что \(2a \leq r\) и \(2b \leq c\).
ВВ выходной файл необходимо вывести три целых числа \(a\), \(b\) и \(s\), удовлетворяющих условиям задачи. Если решений несколько, разрешается вывести любое из них.
Во втором примере облицовка прямоугольника соответствуют следующему рисунку (выступающие за границы прямоугольника части панелей не показаны):

Данная задача содержит семь подзадач. Для оценки каждой подзадачи используется своя группа тестов. Баллы за подзадачу начисляются только в том случае, если все тесты из этой группы пройдены.
В правильном ответе величина сдвига \(s\) равна нулю, \(r\) и \(c\) не превосходят 20.
В правильном ответе величина сдвига \(s\) равна нулю, \(r\) и \(c\) не превосходят 200.
В правильном ответе величина сдвига \(s\) равна нулю, \(r\) и \(c\) не превосходят 1961.
Величина сдвига \(s\) произвольна, \(r\) и \(c\) не превосходят 20.
Величина сдвига \(s\) произвольна, \(r\) и \(c\) не превосходят 200.
Величина сдвига \(s\) произвольна, \(r\) и \(c\) не превосходят 500.
Величина сдвига \(s\) произвольна, \(r\) и \(c\) не превосходят 1961.
2 4 ABAB ABAB
1 2 0
5 7 DCADCAD BABBABB ADCADCA BBABBAB CADCADC
2 3 1
В городе \(\pi\) недавно построили парк аттракционов, в котором есть павильон игровых автоматов. Каждый из автоматов рассчитан на одного человека. В программе Всероссийской олимпиады планируется посещение этого павильона.
Перед организаторами встала сложная задача — составить расписание игры участников олимпиады на автоматах таким образом, чтобы каждый из \(N\) участников олимпиады смог поиграть на каждом из автоматов, и при этом автобус, увозящий участников из парка олимпиады, смог бы отправиться к месту проживания как можно раньше.
Время перемещения участников между автоматами, а также между автобусом и павильоном считается равным нулю. Каждый из участников в любой момент времени может как играть на автомате, так и ждать своей очереди, например, гуляя по парку. Для каждого из \(M\) (\(M \leq N\)) автоматов известно время игры на нём \(t_i\) (\(1 \leq i \leq M\)). Прервать начатую игру на автомате невозможно. Автобус привозит всех участников олимпиады в парк одновременно в нулевой момент времени.
Требуется написать программу, которая по заданным числам \(N\), \(M\) и \(t_i\) определяет оптимальное расписание игры на автоматах для каждого из участников.
В первой строке входного файла содержатся два числа: \(N\) и \(M\) (\(1 \leq M \leq N \leq 100\)). Во второй строке заданы \(M\) целых чисел \(t_i\) (\(1 \leq t_i \leq 100\)), каждое из которых задаёт время игры на \(i\)-м автомате (\(1 \leq i \leq M\)). Числа в строке разделяются одиночными пробелами.
В первой строке необходимо вывести одно число — минимально возможное время отправления автобуса из парка аттракционов. Далее необходимо вывести \(N\) расписаний игр на автоматах, по одному для каждого из участников. Каждое расписание описывается в (\(M + 1\)) строках, первая из которых — пустая, а далее следуют \(M\) строк, описывающих автоматы в порядке их посещения этим участником. Посещение автомата описывается двумя целыми числами: номером автомата \(j\) (\(1 \leq j \leq M\)) и временем начала игры участника на этом автомате.
Данная задача содержит пять подзадач. Для оценки каждой подзадачи используется своя группа тестов. Баллы за подзадачу начисляются только в том случае, если все тесты из этой группы пройдены.
\(M = 1\), \(1 \leq N \leq 100\), \(t_1\) лежит в пределах от 1 до 100.
Все \(t_i\) равны 1, \(N = M\).
Все \(t_i\) равны 1, \(N > M\).
Числа \(t_i\) лежат в пределах от 1 до 100, \(N = M\).
Числа \(t_i\) лежат в пределах от 1 до 100, \(N > M\).
2 1 2
4 1 0 1 2
3 2 2 1
6 1 0 2 2 1 2 2 4 2 0 1 4
Велосипедисты, участвующие в шоссейной гонке, в некоторый момент времени, который называется начальным, оказались в точках, удалённых от места старта на \(x_1\), \(x_2\), ..., \(x_n\) метров (\(n\) – общее количество велосипедистов). Каждый велосипедист двигается со своей постоянной скоростью \(v_1\), \(v_2\), ..., \(v_n\) метров в секунду. Все велосипедисты двигаются в одну и ту же сторону.
Репортёр, освещающий ход соревнований, хочет определить момент времени, в который расстояние между лидирующим в гонке велосипедистом и замыкающим гонку велосипедистом станет минимальным, чтобы с вертолёта сфотографировать сразу всех участников велогонки.
Требуется написать программу, которая по заданному количеству велосипедистов \(n\), заданным начальным положениям велосипедистов \(x_1\), \(x_2\), ..., \(x_n\) и их скоростям \(v_1\), \(v_2\), ..., \(v_n\), вычислит момент времени \(t\), в который расстояние \(l\) между лидирующим и замыкающим велосипедистом будет минимальным.
Первая строка входного файла содержит целое число \(n\) – количество велосипедистов.
В последующих n строках указаны по два целых числа: \(x_i\) – расстояние от старта до \(i\)-го велосипедиста в начальный момент времени (\(0 \leq x_i \leq 10^7\)) и \(v_i\) – его скорость (\(0 \leq v_i \leq 10^7\)).
В выходной файл необходимо вывести два вещественных числа: \(t\) – время в секундах, прошедшее от начального момента времени до момента, когда расстояние в метрах между лидером и замыкающим будет минимальным, \(l\) – искомое расстояние.
Числа t и l должны иметь абсолютную или относительную погрешность не более \(10^{–6}\), что означает следующее. Пусть выведенное число равно \(x\), а в правильном ответе оно равно \(y\). Ответ будет считаться правильным, если значение выражения \(|x – y| / max(1, |y|)\) не превышает \(10^{–6}\).
Данная задача содержит четыре подзадачи. Для оценки каждой подзадачи используется своя группа тестов. Баллы за подзадачу начисляются только в том случае, если все тесты из этой группы пройдены.
\(2 \leq n \leq 50\), \(0 \leq x_i \leq 1000\), \(0 \leq v_i \leq 1000\). Гарантируется, что существует ответ, в котором \(t\) – целое число, не превышающее 1000.
\(2 \leq n \leq 200\).
\(2 \leq n \leq 2000\)
\(2 \leq n \leq 10^5\)
3 0 40 30 10 40 30
1 30
5 90 100 100 70 100 70 110 60 120 35
0.5 5.000000000000
Лесопильный комбинат выполняет заказ на распил брусьев для строительства детского городка. Все готовые брусья должны иметь форму треугольных призм, основаниями которых являются равнобедренные треугольники. Для изготовления брусьев закуплены заготовки в виде половинок продольно распиленных бревен. Заготовки не являются идеальными половинками цилиндров, поэтому при изготовлении бруса необходимо учитывать форму заготовок. Комбинат заинтересован в изготовлении бруса с наибольшей возможной площадью поперечного сечения.
Для каждой заготовки измеряется несколько сечений. Каждое из них задано в виде ломаной, представленной координатами ее вершин (\(x_0, y_0\)), (\(x_1, y_1\)), ..., (\(x_N, y_N\)) в порядке их следования. Координаты вершин ломанной удовлетворяют следующим условиям:
\(x_0 < x_1 < x_2 < \dots < x_N\);
\(x_i = 0\) для некоторого \(0 < i < N\);
\(y_0 = y_N = 0\);
\(y_0 = y_N = 0\);
для всех \(i\) от 1 до (\(N – 1\)) выполнено условие \(y_i > 0\).
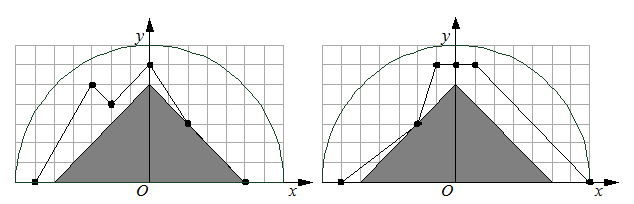
С учетом описанных требований необходимо найти максимально возможную площадь равнобедренного треугольника, удовлетворяющего следующим условиям:
основание треугольника лежит на оси абсцисс;
основание симметрично относительно начала координат;
треугольник полностью лежит внутри каждого из измеренных сечений заготовки.
Требуется написать программу, которая по заданным сечениям заготовки вычислит максимально возможную площадь искомого равнобедренного треугольника.
Первая строка входного файла содержит целое число \(K\) – количество измеренных сечений.
Далее следуют описания каждого из \(K\) сечений. В первой строке описания сечения содержится число \(N_K\) – количество звеньев ломаной. За ней следуют (\(N_K + 1\)) строк, каждая из которых содержит пару целых чисел \(x_i\) и \(y_i\) – координаты вершин ломаной сечения в порядке их следования.
Выходной файл должен содержать одно вещественное число – наибольшую возможную площадь треугольника. Эта площадь должна иметь абсолютную или относительную погрешность не более \(10^{–6}\), что означает следующее. Пусть выведенное число равно \(x\), а в правильном ответе оно равно \(y\). Ответ будет считаться правильным, если значение выражения \(|x – y| / max(1, |y|)\) не превышает \(10^{–6}\).
Данная задача содержит пять подзадач.
\(K = 1\), \(N_1 \leq 15\), координаты вершин по модулю не превышают 20.
Для оценки данной подзадачи используется соответствующая группа тестов. Баллы за подзадачу начисляются только в том случае, если все тесты из этой группы пройдены.
\(1 \leq K \leq 20\), сумма \(N_i \leq 2000\), координаты вершин по модулю не превышают \(10^4\). Гарантируется, что полученный в качестве ответа треугольник является прямоугольным.
Для оценки данной подзадачи используется соответствующая группа тестов. Баллы за подзадачу начисляются только в том случае, если все тесты из этой группы пройдены.
\(1 \leq K \leq 20\), сумма \(N_i \leq 2000\), координаты вершин по модулю не превышают \(10^4\).
Для оценки данной подзадачи используется соответствующая группа тестов. Баллы за подзадачу начисляются только в том случае, если все тесты из этой группы пройдены.
\(1 \leq K \leq 1000\), сумма \(N_i \leq 10^5\), координаты вершин по модулю не превышают \(10^9\). Гарантируется, что полученный в качестве ответа треугольник является прямоугольным.
Для оценки данной подзадачи используется соответствующая группа тестов. Баллы за подзадачу начисляются только в том случае, если все тесты из этой группы пройдены.
\(1 \leq K \leq 1000\), сумма \(N_i \leq 10^5\), координаты вершин по модулю не превышают \(10^9\).
Каждый тест для данной подзадачи оценивается отдельно.
2 5 -6 0 -3 5 -2 4 0 6 2 3 5 0 5 -6 0 -2 3 -1 6 0 6 1 6 7 0
25.0