#112335

Автомат с игрушками

Темы: [Обход в глубину]

Источники: [ Личные олимпиады, Всероссийская олимпиада школьников, Заключительный этап, 2014, 1 тур, Автомат с игрушками ] [ Личные олимпиады, Всероссийская олимпиада школьников, Заключительный этап, 2014, 1 тур, Задача A ]

В развлекательном центре \(Е\)-города был установлен игровой автомат нового поколения. В автомат можно бросить монету и следить за её продвижением сверху вниз по разветвляющемуся лабиринту из трубок. В лабиринте есть n узлов, которые пронумерованы числами от 1 до \(n\). При бросании монета попадает в первый узел. Каждый узел лабиринта, кроме первого, имеет одну входящую сверху трубку, по которой монета может в него попасть. Из каждого узла выходит не более двух трубок, идущих вниз, одна из которых ведет налево, а другая — направо. Каждая трубка имеет некоторую ширину. Монета проваливается в более широкую трубку, а в случае равенства ширины трубок — в левую.

После прохождения монеты по трубке ширина этой трубки уменьшается на 1. Монета не может пройти по трубке ширины 0. Если монета достигла узла, из которого она не может дальше двигаться вниз, автомат останавливается и ждёт, когда в него бросят следующую монету

Изначально в каждом узле лабиринта находится по игрушке. Когда монета попадает в узел первый раз, игрушка, находящаяся в этом узле, достаётся игроку, бросившему эту монету.

Панкрату понравилась игрушка, которая находится в узле с номером \(v\).

Требуется написать программу, которая определяет, сколько монет должен бросить в автомат Панкрат, чтобы получить игрушку из узла \(v\).

Формат входного файла

В первой строке входного файла задано число \(n\) — количество узлов в лабиринте. В последующих n строках заданы описания всех узлов, в \(k\)-й из этих строк описан узел с номером \(k\).

Описание k-го узла состоит из четырех целых чисел: \(a_k\), \(u_k\), \(b_k\), \(w_k\). Если из \(k\)-го узла выходит левая трубка, то \(a_k\) — номер узла, в который она ведет (\(k\) < \(a_k\) <= \(n\)), а \(u_k\) — её ширина. Если левой трубки нет, то \(a_k\) = \(u_k\) = 0. Если из \(k\)-го узла выходит правая трубка, то \(b_k\) — номер узла, в который она ведет (\(k\) < \(b_k\) <= \(n\)), а \(w_k\) — её ширина. Если правой трубки нет, то \(b_k\) = \(w_k\) = 0.

В последней строке задано целое число \(v\) (1 <= \(v\) <= \(n\)) — номер узла, в котором находится игрушка, понравившаяся Панкрату.

Гарантируется, что во все узлы, кроме первого, входит ровно одна трубка

Формат выходного файла

Выходной файл должен содержать одно число — количество монет, которое необходимо бросить в автомат Панкрату, чтобы получить игрушку, которая находится в узле \(v\). Если получить выбранную игрушку невозможно, выведите число −1.

Система оценки

Данная задача содержит две подзадачи. Для оценки каждой подзадачи используется своя группа тестов. Баллы за подзадачу начисляются только в том случае, если все тесты из этой группы пройдены.

Подзадача 1

1 <= \(n\) <= 100

1 <= \(u_k\); \(w_k\) <= 300

Подзадача оценивается в 50 баллов.

Подзадача 2

1 <= \(n\) <= \(10^5\)

1 <= \(u_k\); \(w_k\) <= \(10^9\)

Подзадача оценивается в 50 баллов.

Пояснения к примеру

В первом примере первая монета пройдет лабиринт по следующему пути, и игрок получит игрушки из вершин 1, 3 и 4:

Вторая монета пройдет лабиринт по следующему пути, и игрок получит игрушки из вершин 2 и 6:

Третья монета пройдет лабиринт по следующему пути, и игрок получит игрушки из вершин 5 и 7:

Примеры

Входные данные

Выходные данные

Входные данные

Выходные данные

-1

#112817

Вышивка жемчугом

Темы: [Сканирующая прямая] [Алгоритмы на графах]

Источники: [ Личные олимпиады, Всероссийская олимпиада школьников, Заключительный этап, 2015, 1 тур, Задача C ]

Дано изображение дерева из \(n\) вершин на прямоугольной сетке. Каждое ребро — либо вертикальный, либо горизонтальный отрезок длины \(1\) Дано \(q\) запросов, каждый имеет вид "сколько компонент связности образуется при вырезании данного прямоугольного фрагмента"

Со стародавних времён в поморских деревнях рукодельницы вышивали жемчугом на прямоугольных полотенцах, состоящих из одинаковых клеток. Вышивка начиналась с пришивания жемчужины к полотенцу в центре одной из клеток. Чтобы пришить новую жемчужину, рукодельница делала стежок из клетки, уже содержащей жемчужину, в соседнюю с ней по горизонтали или вертикали свободную клетку. Новая жемчужина пришивалась в центре клетки на конце стежка. Этот процесс повторялся, пока не заканчивались жемчужины.

Одно из таких праздничных полотенец находится в музее. К сожалению, некоторые части узора были утеряны, но описание полотенца сохранилось. Дирекция музея планирует восстановить один из прямоугольных фрагментов полотенца, но не ещё не решила какой именно. Затраты на восстановление фрагмента зависят от количества связных частей узора, попавших на этот фрагмент. Часть узора считается связной, если от любой её жемчужины можно по стежкам перейти к любой другой её жемчужине, не выходя за границы фрагмента. Дирекция всегда относит любые две жемчужины, между которыми можно перейти по стежкам, к одной и той же связной части узора.

Требуется написать программу, вычисляющую количество связных частей узора для каждого из заданных фрагментов.

Входные данные

Первая строка входных данных содержит два целых числа a и b — размеры полотенца в клетках по горизонтали и вертикали.

Вторая строка содержит два числа \(n\) и \(q\) — количество жемчужин в узоре и количество фрагментов соответственно.

Следующие (\(n − 1\)) строк содержат описания стежков. Каждый стежок имеет один из следующих видов:

• \(h \times y\) означает, что клетки с координатами \((x, y)\) и \((x + 1, y)\) содержат жемчужины, соединённые горизонтальным стежком (\(1 \le x \le a − 1; 1 \le y \le b\));

• \(v \times y\) означает, что клетки с координатами \((x, y)\) и \((x, y + 1)\) содержат жемчужины, соединённые вертикальным стежком (\(1 \le x \le a; 1 \le y \le b − 1\)).

Так как неизвестно в каком порядке рукодельница наносила стежки, их описания следуют в произвольном порядке. При этом гарантируется, что узор был получен в результате процесса, описанного в условии задачи.

Следующие \(q\) строк описывают фрагменты. Каждое описание содержит четыре целых числа \(x_1\), \(y_1\), \(x_2\) и \(y_2\) — координаты левой нижней и правой верхней клетки фрагмента (\(1 \le x_1 \le x_2 \le a; 1 \le y_1 \le y_2 \le b\)).

Выходные данные

Выходные данные должны содержать \(q\) строк, где \(i\)-я строка содержит количество связных частей узора в \(i\)-м фрагменте.

Таблица системы оценивания

Замечание

Пояснение к тесту из условия

Примеры

Входные данные

Выходные данные

#113546

Тигры

Темы: [Многоугольники. Выпуклые оболочки] [Интерактивные задачи]

Источники: [ Личные олимпиады, Всероссийская олимпиада школьников, Заключительный этап, 2017, 1 день, Тигры ]

В заповеднике живут q тигров. Чтобы следить за положением тигров на территории заповедника, используются ошейники с радиомаяком. Ошейник у каждого тигра имеет радиомаяк с уникальным сигналом. Система обнаружения настраивается на приём сигнала радиомаяка от i-го тигра последовательно для i от 1 до q.

Для приёма сигнала на территории заповедника установлено n приёмников в точках с координатами (x₁, y₁), ..., (x_n, y_n). Система обнаружения позволяет сотруднику заповедника за один запрос выбрать любые m (3 ≤ m ≤ n) приёмников. Выбранные приёмники должны являться вершинами выпуклого многоугольника. Система определяет, находится ли радиомаяк i-го тигра внутри этого многоугольника.

Сотрудник заповедника должен локализовать положение каждого тигра. Положение i-го тигра считается локализованным, если удалось определить такое множество приёмников, являющихся вершинами выпуклого многоугольника, что внутри этого многоугольника находится тигр, но нет других приёмников.

Для того, чтобы локализовать положение каждого из тигров, сотруднику разрешается сделать не более k запросов.

После того как положение i-го тигра локализовано, система автоматически переходит к приёму сигналов от следующего тигра, пока положение всех q тигров не будет локализовано.

Гарантируется, что никакие три приёмника не лежат на одной прямой, и ни один тигр не находится на прямой, проходящей через два приёмника. Гарантируется, что существует хотя бы один выпуклый многоугольник с вершинами в приёмниках, внутри которого находится тигр.

Требуется написать программу, которая взаимодействует с программой жюри и локализует положение каждого тигра.

Протокол взаимодействия

Это интерактивная задача.

Сначала на вход подаётся информация об установленных в заповеднике приёмниках и количестве тигров.

Первая строка входных данных содержит целое число n — количество приёмников (3 ≤ n ≤ 5 000). Последующие n строк описывают координаты приёмников, j-я из этих строк содержит два целых числа x_j и y_j — координаты j-го приёмника ( - 10⁹ ≤ x_j, y_j ≤ 10⁹). Следующая строка содержит число целое число q — количество тигров (1 ≤ q ≤ 2000).

Для локализации положения тигров необходимо выполнять запросы к системе обнаружения, роль которой выполняет программа жюри.

Для каждого теста зафиксировано число k — максимальное количество запросов к системе обнаружения для локализации положения одного тигра. Гарантируется, что k запросов достаточно, чтобы решить задачу для соответствующих данных. Это число не сообщается программе-решению, но ограничения на него в различных подзадачах приведены в таблице системы оценивания. Если программа-решение делает более k запросов для определения местоположения одного из тигров, на этом тесте она получает в качестве результата тестирования «Неверный ответ».

Запрос к системе обнаружения начинается с символа «?», за которым следует целое число m — количество выбранных в запросе приёмников (3 ≤ m ≤ n), и m различных целых чисел p_i — номера приёмников, перечисленные в порядке обхода многоугольника по или против часовой стрелки (1 ≤ p_i ≤ n).

В ответ программа получает строку «Yes», если тигр находится внутри многоугольника, образованного приёмниками с номерами p₁, ..., p_m, и строку «No» в противном случае.

После того, как положение тигра локализовано, программа-решение должна вывести строку, начинающуюся с символа «!», за которым следует целое число m — количество выбранных приёмников (3 ≤ m ≤ n), и m различных целых чисел p_i — номера приёмников, перечисленные в порядке обхода многоугольника по или против часовой стрелки (1 ≤ p_i ≤ n). Эта строка означает, что внутри выпуклого многоугольника, образованного приёмниками с номерами p₁, ..., p_m, находится тигр и нет других приёмников.

Ответное сообщение от программы жюри отсутствует, и программа-решение должна немедленно приступать к поиску следующего тигра. Локализовав положение тигра с номером q, программа-решение должна завершить работу.

Тигры не перемещаются во время работы системы обнаружения. Координаты тигров в каждом тесте фиксированы и не меняются в процессе тестирования.

Если существует несколько правильных многоугольников, локализующих положение тигра, можно вывести любой из них.

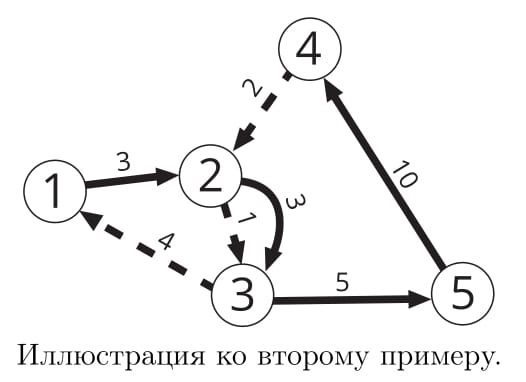
На рисунке продемонстрирована процедура локализации положения каждого из тигров из приведенного ниже примера.

Примечание

Приведённые примеры иллюстрируют взаимодействие программы-решения с программой жюри «по шагам», для чего в них добавлены дополнительные пустые строки. При реальном тестировании лишние пустые строки вводиться не будут, выводить пустые строки также не требуется.

#113547

Путешествие в Метрополис

Темы: [Алгоритм Дейкстры] [Динамическое программирование]

Источники: [ Личные олимпиады, Всероссийская олимпиада школьников, Заключительный этап, 2017, 1 день, Путешествие в Метрополис ]

Путешествие по стране никогда не бывает простым, особенно когда не существует прямого сообщения между городами. Группа туристов хочет добраться в город Метрополис, используя сеть железных дорог, которая соединяет n городов, пронумерованных от 1 до n. Город, из которого выезжает группа, имеет номер 1, Метрополис имеет номер n.

На железной дороге постоянно функционируют m маршрутов поездов. Каждый маршрут определяется последовательностью городов, перечисленных в том порядке, в каком их проезжает поезд, обслуживающий этот маршрут. В каждом маршруте для каждой пары соседних городов задано время, за которое поезд этого маршрута проезжает перегон между этими городами. При этом поезда разных маршрутов могут проезжать один и тот же перегон за разное время.

По пути в Метрополис группа может садиться на поезд и сходить с поезда в любом городе маршрута, не обязательно в начальном или конечном. При этом, можно сойти с поезда маршрута i, пересесть на поезд маршрута j, возможно сделать еще несколько пересадок, а потом вновь сесть в поезд того же маршрута i.

Туристы предъявляют высокие требования к выбору способа проезда в Метрополис.

Во-первых, суммарное время, проведенное в поездах, должно быть минимальным.

Во-вторых, среди всех способов с минимальным временем нахождения в поездах предпочтительным является тот способ, для которого сумма квадратов промежутков времени, непрерывно проведенных в поезде между двумя пересадками, максимальна. Назовём эту сумму качеством путешествия.

Время, проведенное вне поездов, не учитывается.

Требуется написать программу, которая по описаниям имеющихся маршрутов поездов определит минимальное время, которое группе туристов придется провести в поездах, а также максимальное качество путешествия с таким временем.

Входные данные

В первой строке входных данных заданы два целых числа (2 ≤ n ≤ 10⁶, 1 ≤ m ≤ 10⁶) — количество городов и количество маршрутов соответственно.

Далее в m строках содержится описание маршрутов.

Описание каждого маршрута начинается с целого числа s_i — количество перегонов в маршруте с номером i (1 ≤ s_i ≤ 10⁶). Далее следуют (2s_i + 1) целых чисел, описывающих города маршрута и время проезда перегона между соседними городами маршрута, в следующем порядке: v_i, 1, t_i, 1, v_i, 2, t_i, 2, v_i, 3, ..., t_{i, s_i}, v_{i, s_i + 1}, где v_i, j — номер j-го города маршрута, t_i, j — время проезда перегона между j-м и (j + 1)-м городом (1 ≤ v_i, j ≤ n, 1 ≤ t_i, j ≤ 1000).

Гарантируется, что s₁ + s₂ + ... + s_m ≤ 10⁶. Никакие два города в описании маршрута не совпадают. Гарантируется, что с помощью имеющихся маршрутов можно добраться из города с номером 1 в город с номером n.

Выходные данные

Выходные данные должны содержать два целых числа — минимальное суммарное время, которое придется провести в поездах, и максимальное качество пути с таким временем.

Примечание

В первом примере группа туристов отправится прямым маршрутом в Метрополис.

Во втором примере не оптимально проехать напрямую по первому маршруту, так как время в поезде при этом не будет минимальным возможным. Поэтому они отправятся на поезде по маршруту 1 из города 1 в город 2, затем на поезде по маршруту 2 из города 2 в город 3, а затем снова на поезде по маршруту 1 из города 3 в город 5. При этом сумма квадратов промежутков времени, проведенных в поездах между пересадками, равна 3² + 1² + 5² = 35.

В третьем примере добраться из города 1 в город 4 за минимальное время можно, пересаживаясь с маршрута 1 на маршрут 2 в любом из городов 2, 3 или 4. Максимальное качество путешествия достигается при пересадке в городе 2: 1² + 9² = 82.

Обратите внимание, что второй и третий примеры не удовлетворяют ограничениям первой и второй подзадачи, решение будет протестировано на этих подзадачах, если оно пройдет первый тест из примера. Все тесты из примера подходят под ограничения подзадач 3 – 7, решение будет проверяться на тестах этих подзадач только в случае прохождения всех тестов из примера.

Примеры

Входные данные

2 1
1 1 3 2

Выходные данные

3 9

Входные данные

5 2
4 1 3 2 3 3 5 5 10 4
3 4 2 2 1 3 4 1

Выходные данные

9 35

Входные данные

5 2
3 1 1 2 2 3 3 4
3 2 2 3 3 4 4 5

Выходные данные

10 82

#113549

Серверы на Меркурии

Темы: [Динамическое программирование]

Источники: [ Личные олимпиады, Всероссийская олимпиада школьников, Заключительный этап, 2017, 2 день, Серверы на Меркурии ]

Компьютерная система управления станциями на Меркурии состоит из n серверов, пронумерованных от 1 до n. Серверы соединены (n - 1) двусторонними каналами связи, i-й из которых соединяет i-й и (i + 1)-й серверы.

С Земли необходимо передать пакет обновления программного обеспечения для компьютерной системы управления. Пакет необходимо установить на каждый сервер. Стоимость передачи пакета обновления с Земли на Меркурий очень высока, поэтому с Земли пакет обновления передаётся только на один сервер. Затем пакет необходимо передать на все остальные серверы по каналам связи, возможно, через другие серверы.

Из-за высокой солнечной радиации на Меркурии передавать пакет обновления по каналам связи можно только в некоторые промежутки времени. Для i-го канала связи известен промежуток времени [l_i, r_i], во время которого возможна передача пакета по этому каналу. Пакет передаётся по любому каналу связи мгновенно.

Пакет обновления, переданный на j-й сервер, немедленно устанавливается и помещается в специальный буфер памяти, из которого он может быть передан на другие серверы. Пакет находится в буфере памяти j-го сервера в течение t_j секунд с момента его получения. Если в момент нахождения пакета в буфере памяти сервера появляется возможность передать его по каналу связи на соседний сервер, на котором пакет обновления пока не установлен, то он немедленно передаётся по этому каналу связи.

Поскольку пакет содержит важные обновления, требуется начать его распространение как можно раньше.

Требуется написать программу, которая для всех i от 1 до n определяет, возможно ли установить пакет обновления на все серверы, передав его с Земли на i-й сервер. Если это возможно, то необходимо определить, в какой минимальный неотрицательный момент времени можно установить пакет на этот сервер, чтобы в результате обновление оказалось установлено на всех серверах.

Входные данные

Первая строка входных данных содержит n — количество серверов (1 ≤ n ≤ 200 000).

Вторая строка содержит n целых чисел t₁, t₂, ..., t_n, где t_j — время нахождения пакета в буфере памяти j-го сервера (0 ≤ t_j ≤ 10⁹).

Следующие (n - 1) строк описывают каналы связи. Для описания i-го канала задаются два целых числа l_i и r_i — границы промежутка времени, на протяжении которого возможна передача пакета по этому каналу (0 ≤ l_i ≤ r_i ≤ 10⁹).

Выходные данные

Выходные данные должны содержать n целых чисел a₁, a₂, ..., a_n.

Число a_i должно быть равно такому минимальному неотрицательному моменту времени, что при установке пакета обновления на i-й сервер в момент a_i, пакет будет в итоге установлен на всех серверах. Если такого момента времени для i-го сервера не существует, необходимо вывести a_i = - 1.

Примечание

В первом примере имеется всего один сервер, минимальное подходящее время, в которое можно установить на него обновление — 0.

Во втором примере есть два сервера, передать обновление между которыми можно в промежуток от 6 до 8. Первый сервер хранит обновление в буфере 3 единицы времени, а второй — 5 единиц времени. Если отправить обновление первому серверу в момент 3, то он передаст его второму серверу в момент 6. Аналогично если отправить обновление второму серверу в момент 1, то он передаст его первому серверу в момент 6.

В третьем примере нельзя передать обновление первому серверу так, чтобы оно передалось третьему серверу, так как канал 2–3 закрывается до того, как открывается канал 1–2. Можно отправить обновление второму или третьему серверу в момент 5. В этот момент канал 2–3 открыт, поэтому его сразу получат второй и третий серверы. В момент 7, когда откроется канал 1–2 обновление ещё будет находиться в буфере второго сервера, и передастся первому серверу.

В четвёртом примере второй сервер хранит пакет 0 единиц времени, а канал 2–3 открыт в промежуток 5–5. Чтобы передать обновление через второй сервер к третьему серверу, оно должно попасть ко второму серверу в момент 5. Если же мы хотим отправить обновление третьему серверу, то это можно сделать в момент 4, при этом оно будет храниться до момента 7 и будет в итоге установлено на все серверы.

Примеры

Входные данные

1
10

Выходные данные

Входные данные

2
3 5
6 8

Выходные данные

3
1

Входные данные

Выходные данные

-1
5
5

Входные данные

Выходные данные