Составьте программу, которая по координатам вершин треугольника находит длину L стороны квадрата минимальной площади, в который можно поместить этот треугольник. L достаточно найти с точностью 10-4.
Файл содержит в одной строке действительные числа X1 Y1 X2 Y2 X3 Y3, разделенные пробелами, – координаты вершин треугольника (-10000 X1, Y1, X2, Y2, X3, Y3 10000).
Файл должен содержать одно число - длину L стороны искомого квадрата.
0.0 0.0 1.1 0.0 0.0 1.1
1.100000000
На плоскости задано такое множество из N многоугольников, что выполняются следующие условия:
Напишите программу, которая для каждого многоугольника выдает количество многоугольников, внутри которых он находится.
Первая строка входного файла содержит целое число N — количество многоугольников, 3≤N≤100000. Следующие N строк файла описывают N многоугольников. (i+1)–ая строка файла описывает i–ый многоугольник. Первое целое число Ci — количество вершин многоугольника, 3≤Ci≤20. Последующие Ci пар чисел — координаты вершин многоугольника в порядке его обхода. Координаты вершин — целые числа, принадлежащие диапазону от -2 000 000 000 до 2 000 000 000.
Единственная строка выходного файла должна содержать N чисел: i–ое число строки должно быть Pi — количество многоугольников, внутри которых находится i–ый многоугольник.
3 3 -2 1 8 9 12 1 3 7 5 6 3 7 4 4 4 3 7 7 9 3 1 2
0 2 1
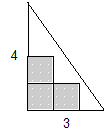Территория Великой Треугольной Области (ВТО) представляет собой прямоугольный треугольник. Длины его катетов равны M и N государственных единиц длины (ГЕД). Правительство ВТО решило покрыть как можно большую часть территории области квадратными плитами размером 11 ГЕД. Плиты должны плотно прилегать друг к другу и к катетам ВТО. Разрезать плиты нельзя.
Согласно межгосударственным соглашениям, правительство ВТО не имеет права покрыть частью своей плиты чужую территорию. Производитель поставляет плиты только контейнерными партиями — по P плит. Правительство заказывает столько контейнеров, сколько необходимо для реализации проекта.
Заведующий центральным складом, узнав про проект, решил, что его интересует количество плит, которые останутся на складе из последнего контейнера после покрытия территории ВТО.
Напишите программу, которая по длинам катетов ВТО и вместимости контейнера находит количество плит, которые останутся на складе после осуществления проекта.
Единственная строка входного файла содержит три целых числа: M, N (2≤M, N≤2 000 000 000) и P (100≤P≤10 000).
Единственная строка выходного файла должна содержать целое число — количество неиспользованных плит из последнего контейнера.
4 3 100
97
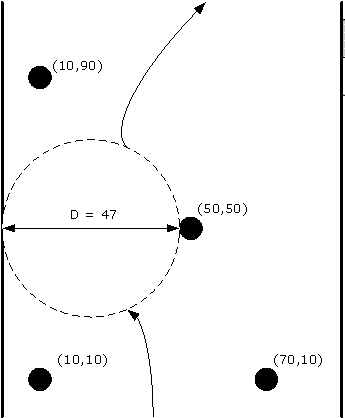Единственный способ попасть в Зал Круглых Столов – пройти через Колонный Коридор. Стены Коридора изображаются на карте прямыми линиями, которые параллельны оси OY системы координат. Вход в Коридор находится снизу, а выход из Коридора в Зал – сверху. В Коридоре есть цилиндрические (на карте круглые) Колонны одинакового радиуса R.
Напишите программу, которая по информации о размерах Коридора, и размещения Колонн определяет диаметр наибольшего из Круглых Столов, который можно пронести через такой Коридор, сохраняя поверхность Стола горизонтальной.
В первой строке входного файла заданы два числа XL и XR – x-координаты левой и правой стен Коридора. Во второй строке находится целое число R (1≤R≤1 000 000) – радиус всех Колонн. В третей – целое число N (1≤N≤200), которое задает количество Колонн. Далее следуют N строк, в каждой из которых по два числа – x- и y-координаты центра соответствующей Колонны.
Все входные координаты – целые числа, которые по модулю не превосходят 1 000 000.
Единственная строка выходного файла должна содержать одно число – искомый диаметр наибольшего Стола. Диаметр следует выводить с точностью 3 знака после десятичной точки (даже в случае, когда он окажется целым). Если нельзя пронести ни одного Стола, то ответ должен быть: 0.000
Точность 3 знака после точки, по обычным правилам округления, обозначает, что ответ, который выдается в выходной файл, должен отличаться от точного не более чем на 510-4 (т.е. на 0.0005). Например, если точный ответ 1.234567, то в файле должно находится число 1.235. Если точный ответ 5.0005, то необходимо округлять в большую сторону, т.е. в файл следует выдать 5.001
0 90 3 4 10 10 70 10 50 50 10 90
47.000
На плоскости заданы N разных окружностей. Две окружности пересекаются, если они имеют хотя бы одну общую точку.
Напишите программу, которая по координатам центров окружностей и их радиусам найдет пару пересекающихся окружностей.
В первой строке входного файла содержится целое числоN (1≤N≤10 000) . В каждой из последующих N строк содержатся три натуральных числа X, Y, R меньших 10 000, которые задают координаты центра окружности (X, Y) и его радиус R.
Единственная строка выходного файла должна содержать пару номеров пересекающихся окружностей, либо единственное число 0, если никакие две окружности не пересекаются. Окружности нумеруются соответственно порядку во входном файле, начиная с 1 до N. Если существует несколько пар пересекающиеся окружностей, выведите любую из них. Элементы пары могут быть выведены в произвольном порядке.
5 5 10 4 6 20 3 10 15 3 12 8 2 13 13 1
5 3