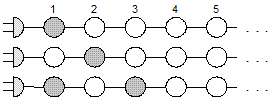
 Новогодняя елка украшена гирляндой бесконечной длины, которая состоит из последовательно соединенных лампочек. Когда гирлянду включают, загорается только первая лампочка, считая от выключателя, которая горит одну секунду. Далее гирлянда начинает мигать по следующему правилу. Каждую секунду для каждой лампочки проверяется условие: если ровно одна из ее соседних лампочек горит, то эта лампочка будет гореть на следующей секунде; иначе – не будет гореть. У первой лампочки только одна соседняя.
Новогодняя елка украшена гирляндой бесконечной длины, которая состоит из последовательно соединенных лампочек. Когда гирлянду включают, загорается только первая лампочка, считая от выключателя, которая горит одну секунду. Далее гирлянда начинает мигать по следующему правилу. Каждую секунду для каждой лампочки проверяется условие: если ровно одна из ее соседних лампочек горит, то эта лампочка будет гореть на следующей секунде; иначе – не будет гореть. У первой лампочки только одна соседняя.
Напишите программу, которая по номеру секунды находит количество лампочек гирлянды, которые будут гореть на протяжении этой секунды.
Единственная строка входного файла содержит одно целое число N (1≤N≤109) – номер секунды.
Единственная строка выходного файла должна содержать целое число – количество лампочек, которые будут гореть на секунде N.
7
4
5
2
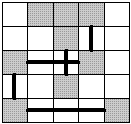 Чтобы не отставать от современной мировой тенденции, правительство страны Олимпия планирует построить несколько островов для привлечения туристов. Карта островов уже подготовлена и представляет собой таблицу размером NM клеток. Каждая клетка может быть водой или сушей. Набор клеток, которые представляют сушу, есть островом, когда из любой из них можно попасть в любую другую, перемещаясь по соседним по горизонтали или вертикали клеткам, и не существует других таких клеток вне набора.
Чтобы не отставать от современной мировой тенденции, правительство страны Олимпия планирует построить несколько островов для привлечения туристов. Карта островов уже подготовлена и представляет собой таблицу размером NM клеток. Каждая клетка может быть водой или сушей. Набор клеток, которые представляют сушу, есть островом, когда из любой из них можно попасть в любую другую, перемещаясь по соседним по горизонтали или вертикали клеткам, и не существует других таких клеток вне набора.
Для удобства было решено построить мосты между некоторыми островами так, чтобы все острова стали связанными между собой. Мосты должны строиться только по вертикали или горизонтали, проходить только по клеткам с водой, начинаться и заканчиваться клетками с сушей. За стоимость строительства моста можно считать количество клеток воды, через которые он проходит. Требуется найти минимальную возможную общую стоимость строительства группы мостов, которые связывали бы между собой все острова. Другими словами, чтобы из каждой клетки суши можно было достичь любой другой, перемещаясь по соседним по вертикали и горизонтали клеткам суши, либо мостам. Два разных моста могут пересекаться между собой, т.е. проходить через одну и ту же самую клетку воды на разных уровнях.
Напишите программу, которая по карте островов находит минимальную стоимость строительства группы мостов, которые соединяют все острова.
Первая строка выходного файла содержит два целых числа N и M (1≤N, M≤500) – размеры карты островов. Каждая из последующих N строк содержит M символов 0 (вода) либо 1 (суша).
Единственная строка выходного файла должна содержать одно целое число – найденную минимальную стоимость строительства мостов. Если соединить острова мостами невозможно, требуются вывести число -1.
5 5 01110 00100 10010 00100 10001
8
На планете Олимпия завершено изучение генома обитателей Олимпийской галактики. Оказалось, что расшифрованный геном может быть представлен в виде набора целых чисел, которые могут повторяться. В представлении генома талантливой личности содержится среди прочих единственное число, которое встречается нечетное количество раз и задает номер определенного генетически обусловленного таланта.
Разработанное оборудование получает представление генома в виде набора множеств чисел. Каждое множество задается четверкой чисел s, f, a, b. Такому множеству принадлежат a последовательных целых чисел начиная с s, следующие b чисел множеству не принадлежат, следующие a снова принадлежат, и т.д. Все числа множества не превышают f. Например, множество (s=1, f=10, a=2, b=1) содержит числа: 1, 2, 4, 5, 7, 8, 10, а множество (s=5, f=50 a=1, b=19) числа: 5, 25, 45.
Напишите программу GENOME, которая по представлению генома в виде набора множеств чисел установит, обладает ли его владелец каким-то генетически обусловленным талантом, и определит его номер.
Первая строка входного файла содержит количество множеств N (1≤N≤10 000) в наборе. Последующие N строк задают сами множества. Каждое множество задается четверкой чисел – s, f, a, b, (1≤s, f, a, b<109; s≤f). Гарантируется, что представление генома содержит не больше одного числа, которое встречается нечетное количество раз.
Единственная строка выходного файла GENOME.SOL должна содержать целое число, которое встречается нечетное количество раз в представлении генома, либо 0, если такого числа не существует.
4 7 59 1 9 7 82 1 49 17 50 1 29 27 27 1 1
37
Посетив перед Новым годом большой магазин, вы выбрали много подарков родным и друзьям. Сэкономить определенное количество денег вам могут помочь два типа предновогодних скидок, которые действуют в магазине:
1. При покупке трех товаров вы платите за них как за два самых дорогих из них.
2. При покупке четырех товаров вы платите за них как за три самых дорогих из них.
Таким образом, определенные товары можно объединить в тройки либо четверки и заплатить за них меньше. Требуется определить наименьшую возможную сумму денег, которая будет потрачена на приобретение всех подарков. Например, если цены пяти выбранных подарков составляют: 50, 80, 50, 100, 20, то можно отдельно купить четыре первых товара, получить за них скидку, и потом купить оставшийся подарок по его номинальной цене. В целом вся покупка будет стоить 250 денежных единиц, вместо 300.
Напишите программу, которая по ценам всех подарков, находит минимальную сумму денег, достаточную для их покупки.
Первая строка входного файла содержит одно целое число N (0≤N≤10 000). Вторая строка содержит N натуральных чисел – цены подарков. Сумма цен всех подарков меньше чем 109. Объединять можно не только те товары, которые идут подряд во входных данных.
Единственная строка выходного файла должна содержать одно целое число – найденную минимальную сумму денег, за которую можно купить все подарки.
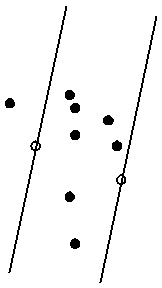 На плоскости задано N точек. Кроме того, на плоскости заданы две базовые точки.
На плоскости задано N точек. Кроме того, на плоскости заданы две базовые точки.
Напишите программу, которая находит максимальное количество точек, которые попадут в полосу образованную парой параллельных прямых произвольно проведенных через базовые точки. Базовые точки не нужно включать в сумму точек. Если точка лежит на прямой – ее необходимо включить в сумму.
Первая строка входного файла содержит одно целое число N (0≤N≤10000) – количество точек. Вторая строка содержит координаты двух базовых точек в формате x1 y1 x2 y2. Каждая из последующих N строк содержит координаты точки плоскости в формате x y. Координаты точек – целые числа, по модулю не превышающие 10000. Базовые точки отличаются, по крайней мере, одной координатой.
Единственная строка выходного файла должна содержать целое число – найденное максимальное количество точек, которые попадут в полосу, образованную оптимально проведенными параллельными прямыми через базовые точки.
4 0 0 50 0 0 -50 -1 0 50 0 100 50
3