2010(6 задач)
2011(6 задач)
2012(6 задач)
2013(6 задач)
XI Нижегородская городская олимпиада по информатике им. В. Д. Лелюха, 2015г.(6 задач)
XII Городская олимпиада школьников по информатике им. В. Д. Лелюха, 2016 г.(6 задач)
Мальчик Влад недавно побывал в Японии и привёз оттуда новую жевательную резинку. Вернувшись в университет после поездки, на первой же паре Влад раздал жвачку всем своим \((N-1)\) однокурсникам и взял одну себе. Дождавшись момента, когда лектор отвернулся к доске, на счёт “три-четыре” все \(N\) студентов дружно начали надувать пузыри. Известно, что \(i\)-й студент надувает пузырь до максимально возможного размера за время \(t_i\), после чего пузырь мгновенно лопается, и студент начинает надувать пузырь заново с той же скоростью.
Всё это время преподаватель настолько увлечён тонкостями квантового математического анализа, что не слышит ничего происходящего в аудитории. И только когда все \(N\) пузырей лопнут одновременно, преподаватель услышит шум и обернётся. И уж тогда студентам достанется, а больше всех тому, кто принёс на пару \(N\) жевательных резинок.
Определите, сколько времени студенты смогут наслаждаться надуванием пузырей, не замечаемые преподавателем.
Например, если \(N=2\), \(t_1=2\), \(t_2=3\), то будет происходить следующее:
Первый студент надувает пузырь с момента времени \(t=0\) до момента времени \(t=2\), потом пузырь лопается, и он надувает пузырь заново — с момента времени \(t=2\) до момента времени \(t=4\), а потом ещё раз — с момента времени \(t=4\) до \(t=6\).
Второй студент надувает пузырь с \(t=0\) до \(t=3\) и ещё раз с \(t=3\) до \(t=6\).
В момент \(t=6\) пузыри лопаются одновременно у обоих студентов, преподаватель оборачивается и говорит: “Всё, Влад! Ты меня достал!”.
На первой строке входного файла находится одно целое число \(N\) — количество студентов (\(1\leq N \leq 10\,000\)). Следующие \(N\) строк содержат по одному целому числу \(t_1\), \(t_2\), ..., \(t_N\). Гарантируется, что \(1\leq t_i \leq 1000\).
Выведите в выходной файл одно число — время, в течение которого студенты во главе с Владом могут наслаждаться безнаказанным надуванием пузырей.
2 2 3
6
1 1
1
2 16 1
16
3 627 182 85
9699690
У мальчика Васи есть \(N\) шоколадок (возможно, разного веса). Вася пригласил к себе в гости \(K\) своих друзей и хочет подарить им шоколадки. Чтобы никому из друзей не было обидно, Вася решил раздать шоколадки так, чтобы каждому другу досталось одно и то же количество шоколада (т.е. суммарный вес шоколадок, доставшихся каждому другу, должен быть одинаковым). Вася может раздать все свои шоколадки, может раздать лишь часть, но, поскольку он — очень гостеприимный мальчик, он не хочет оставлять друзей совсем без шоколада (т.е. сумма весов шоколадок, доставшихся каждому другу, должна быть строго положительной). Все шоколадки красиво упакованы, т.е. делить их на части нельзя.
Определите, сколько у Васи есть способов раздать шоколад своим друзьям. Два способа считайте различными тогда и только тогда, когда существует шоколадка, которая в одном способе досталась некоторому другу, а в другом — другому другу или вовсе не была отдана друзьям.
В первой строке входного файла находятся два натуральных числа \(N\) и \(K\) (\(1 \leq N \leq 15\), \(1 \leq K \leq 15\)) — количество шоколадок у Васи и количество друзей, которых Вася пригласил в гости. Во второй строке содержатся \(N\) натуральных чисел — веса шоколадок. Ни один из весов не превосходит \(1000\).
Выведите в выходной файл одно число — количество способов раздать шоколадки друзьям.
Во втором примере возможные распределения шоколадок следующие:
5 4 1 2 1 1 1
24
3 2 1 1 2
4
Капитаны Флинт и Джек Воробей нашли клад и хотят поделить его. Клад находится в шкатулке и состоит из чётного числа драгоценных камней. Капитан Флинт оценил \(i\)-ый камень в \(a_i\) пиастров, а Джек Воробей — в \(b_i\) долларов. Теперь они действуют следующим образом. Джек Воробей достаёт из шкатулки два камня, после чего Флинт забирает себе один из них (естественно, тот, у которого больше \(a_i\)). Оставшийся камень достаётся Воробью. После этого Джек Воробей достаёт ещё пару камней, и так далее: каждым ходом Воробей достает из шкатулки два камня, Флинт забирает себе камень с большим \(a_i\), оставшийся камень достается Воробью.
Джек Воробей знает все \(a_i\), все \(b_i\), а также может, доставая очередные два камня, подглядеть в шкатулку и выбрать, какие именно камни надо доставать. Помогите ему действовать так, чтобы доля Воробья была максимально возможной (т.е. чтобы сумма \(b_i\) полученных Воробьём камней была как можно больше).
По сравнению с камнями шкатулка ничего не стоит, поэтому её можно не учитывать при дележе.
Первая строка входного файла содержит одно целое число \(N\) — количество камней в кладе. Гарантируется, что \(N\) чётное и что \(2\leq N\leq 5000\). Далее следуют две строки по \(N\) целых чисел в каждой: сначала заданы все \(a_i\), потом — все \(b_i\). Гарантируется, что все \(a_i\) различны (т.е. что действия Флинта всегда однозначно определены). Гарантируется, что все \(a_i\) и все \(b_i\) положительны и не превосходят \(400\,000\).
В выходной файл выведите \(N/2\) строк по два числа в каждой — пары камней, в том порядке, как их должен доставать из шкатулки Джек Воробей. Камни нумеруются начиная с 1.
Числа в пределах каждой пары можете выводить в произвольном порядке. Если есть несколько оптимальных решений, выводите любое.
Среди тестов будут такие, в которых каждый камень оба капитана оценивают одинаково: \(a_i=b_i\) для каждого \(i\) (как во втором тесте из примера); суммарная стоимость таких тестов будет 40 баллов.
6 6 10 11 18 5 14 1 7 6 12 15 16
5 1 2 3 6 4
6 6 44 2 43 7 48 6 44 2 43 7 48
3 1 5 4 2 6
В фирме, в которой работает ваш друг, ввели новый дизайн билетов на маршрутки. Теперь номер билета может быть любым натуральным числом. Радостные пассажиры тут же придумали новый, очень простой способ определения счастливости номера билета. Он состоит в следующем. Пусть номер билета равен \(N\). Если \(N<10\), то счастливость числа \(N\) (т.е. и самого билета) равна \(N\), иначе: посчитаем сумму цифр числа \(N\), пусть она равна \(S\) — тогда счастливость числа \(N\) будет равна счастливости числа \(S\).
Например, счастливость билета с номером \(7351\) равна счастливости билета с номером \(16\) (т.к. \(7+3+5+1=16\)), а она в свою очередь равна счастливости билета с номером 7 (т.к. \(1+6=7\)), а последняя просто равна 7 (т.к. \(7<10\)).
Такое определение счастливости вполне устроило обычных пассажиров маршрутки, но совсем не устроило большинство студентов, которые быстро нашли способ без особенных усилий определять счастливость билета. Поэтому, используя это определение, они придумали новую игру: обладатель билета должен разложить его номер в сумму нескольких чисел так, чтобы суммарная счастливость слагаемых была максимальна.
Но и эта игра устроила не всех студентов. Наиболее активные из них заметили, что игра становится ещё более интересной, если раскладывать \(N\) не в сумму, а в произведение чисел, с целью, по-прежнему, максимизировать сумму счастливостей множителей.
Напишите программу, которая будет решать эту задачу, т.е. по данному \(N\) находить такое его представление \(N=a_1\cdot a_2\cdot \ldots\), где все \(a_i\) натуральны, больше единицы, и суммарная счастливость чисел \(a_1\), \(a_2\), ... максимальна.
Для вашего удобства номер билета \(N\) задан его разложением на простые множители. Таким образом, первая строка входного файла содержит одно натуральное число — количество множителей в разложении числа \(N\) на простые, а далее следуют сами множители. \(N\) не превосходит \(10^{18}\), а каждый простой множитель не превосходит \(10^9\).
Если оптимальных решений несколько, выведите любое.
В выходной файл выведите искомое разложение \(N\) на множители. А именно, сначала выведите количество множителей в вашем разложении, а потом — сами множители.
Если ваша программа будет проходить тесты, в которых \(N\leq 10^9\), то она получит не менее 30 баллов.
3 2 2 3
2 6 2
2 2 11
2 2 11
Большое количество соревнований по разным видам спорта проводится по так называемой “олимпийской системе”. В простейшем варианте она состоит в следующем. В турнире участвуют \(N=2k\) игроков. Они получают номера от 1 до \(N\), и в первом круге игрок 1 играет с игроком 2, игрок 3 — с игроком 4 и т.д., игрок (\(N−1\)) — с игроком \(N\). Проигравшие в каждой паре выбывают из соревнований, а победители проходят во второй круг. Там победитель первой пары (т.е. игрок 1 или игрок 2) играет с победителем второй пары и т.д. Таким образом, в первом круге участвуют \(N=2k\) игроков, во втором круге — N2=2k−1 и т.д., в последнем круге (финале) участвуют два игрока.
Серьёзной проблемой при организации соревнований по олимпийской системе является то, что некоторые сильные игроки могут встретиться между собой уже в одном из первых кругов, в результате чего некоторые сильные участники могут рано выбыть из борьбы, в то время как другие, менее сильные участники могут пройти намного выше, если им повезёт с соперниками. Для борьбы с этим эффектом применяется так называемый “рассев” игроков, когда начальная нумерация участников не является полностью случайной, и вероятность “везения”/“невезения” с соперниками резко уменьшается.
В этой задаче вам нужно будет написать программу, находящую в некотором смысле оптимальный “рассев” игроков. Для этого рассмотрим следующую модель.
Предположим, что участников можно упорядочить по силе так, что более сильный игрок всегда будет выигрывать у более слабого. В таком случае по изначальному “рассеву” игроков дальнейший ход соревнований будет однозначно определён. Тогда в качестве критерия оптимальности “рассева” можно потребовать выполнение следующих условий:
* в финале играют двое сильнейших игроков,
* в полуфиналах играют четверо сильнейших игроков,
* и т.д.: в каждом круге играют только сильнейшие игроки (т.е. если в каком-то круге n мест, то в этом круге должны участвовать n сильнейших игроков).
Вам дано \(N\). Найдите хотя бы один оптимальный рассев.
Входной файл содержит одно число \(N\) — количество участников соревнований. Гарантируется, что \(N\) будет степенью двойки и что \(1\leq N\leq 2^{17}\).
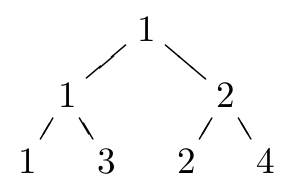
Занумеруем игроков по их силе от 1 до \(N\) (1 — наиболее сильный, \(N\) — наименее). Выведите в выходной файл оптимальный “рассев” участников, т.е. выведите \(N\) чисел, \(i\)"=ое из которых будет номером игрока, который должен стоять на \(i\)"=м месте в оптимальном “рассеве”.
Если существует несколько оптимальных “рассевов”, выведите любой. Если оптимального “рассева” не существует, выведите в выходной файл одно число \(-1\).
4
1 3 2 4