Сегодня на уроке математики Петя и Вася изучали понятие
арифметической прогрессии. Арифметической прогрессией с разностью d
называется последовательность чисел a1, a2, …, ak,
в которой разность между любыми двумя последовательными числами равна
d. Например, последовательность 2,
5, 8, 11 является арифметической прогрессией с разностью 3.
После
урока Петя и Вася придумали новую игру с числами. Игра проходит
следующим образом.
В
корзине находятся n фишек, на
которых написаны различные целые числа a1,
a2, …, an.
По ходу игры игроки выкладывают фишки из корзины на стол. Петя и Вася
делают ходы по очереди, первым ходит Петя. Ход состоит в том, что
игрок берет одну фишку из корзины и выкладывает ее на стол. Игрок
может сам решить, какую фишку взять. После этого он должен назвать
целое число d ≥ 2
такое, что все числа на выбранных к данному моменту фишках являются
членами некоторой арифметической прогрессии с разностью d,
не обязательно последовательными. Например, если на столе выложены
фишки с числами 2, 8 и 11, то можно назвать число 3, поскольку эти
числа являются членами приведенной в начале условия арифметической
прогрессии с разностью 3.
Игрок
проигрывает, если он не может сделать ход из-за отсутствия фишек в
корзине или из-за того, что добавление любой фишки из корзины на стол
приводит к тому, что он не сможет подобрать соответствующее число d.
Например,
если в корзине имеются числа 2, 3, 5 и 7, то Петя может выиграть. Для
этого ему необходимо первым ходом выложить на стол число 3. После
первого хода у него много вариантов назвать число d,
например он может назвать d = 3.
Теперь у Васи два варианта хода.
- Вася может вторым
ходом выложить фишку с числом 5 и назвать d
= 2. Тогда Петя выкладывает фишку с числом 7, называя d
= 2. На столе оказываются фишки с числами 3, 5 и 7, а в корзине
осталась только фишка с числом 2. Вася не может ее выложить,
поскольку после этого он не сможет назвать корректное число d.
В этом случае Вася проигрывает.
- Вася может вторым
ходом выложить фишку с числом 7 и также назвать, например, d
= 2. Тогда Петя выкладывает фишку с числом 5, называя также d
= 2. Вася снова попадает в ситуацию, когда на столе оказываются
фишки с числами 3, 5 и 7, а в корзине осталась только фишка с числом
2, и он также проигрывает.
Заметим,
что любой другой первый ход Пети приводит к его проигрышу. Если он
выкладывает число 2, то Вася отвечает числом 7, и Петя не может
выложить ни одной фишки. Если Петя выкладывает фишку с числом 5 или
7, то Вася выкладывает фишку с числом 2, и у Пети также нет
допустимого хода.
Требуется
написать программу, которая по заданному количеству фишек n
и числам на фишках a1,
a2, …, an
определяет, сможет ли Петя выиграть вне зависимости от действий Васи,
и находит все возможные первые ходы Пети, ведущие к выигрышу.
Выходные данные
Первая
строка выходного файла должна содержать число k
— количество различных первых ходов, которые может сделать
Петя, чтобы выиграть. Если Вася может выиграть вне зависимости от
действий Пети, строка должна содержать цифру 0.
Во
второй строке должно содержаться k
различных целых чисел — все выигрышные числа. Будем называть
число выигрышным, если, выложив в качестве первого хода фишку,
содержащую это число, Петя может выиграть вне зависимости от действий
Васи. Соседние числа в строке должны быть разделены ровно одним
пробелом.
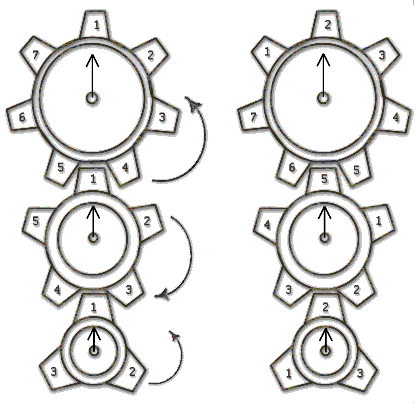 На каждой из трех осей установлено по одной вращающейся шестеренке и неподвижной стрелке. Шестеренки соединены последовательно. На первой шестеренке n зубцов, на второй — m, на третьей — k. На каждом зубце первой, второй и третьей шестеренок по часовой стрелке написаны в порядке возрастания числа от 1 до n, от 1 до m и от 1 до k соответственно. Стрелки зафиксировали таким образом, что когда стрелка первой оси указывает на число, стрелки двух других осей также указывают на числа. Витя записывает три числа (a1,a2,a3), на которые указывают стрелки. После этого он поворачивает первую шестеренку на угол 360°/n против часовой стрелки, чтобы напротив стрелки на первой оси оказался следующий (по часовой стрелке) зубец. При этом вторая шестеренка поворачивается на угол 360°/m по часовой стрелке (размеры зубцов у шестеренок одинаковые, поэтому размеры самих шестеренок разные, чтобы на границе шестеренок равномерно уложилось разное число одинаковых по размеру зубцов), а третья шестеренка поворачивается на угол 360°/k против часовой стрелки. Витя опять записывает три числа, на которые указывают стрелки.
На каждой из трех осей установлено по одной вращающейся шестеренке и неподвижной стрелке. Шестеренки соединены последовательно. На первой шестеренке n зубцов, на второй — m, на третьей — k. На каждом зубце первой, второй и третьей шестеренок по часовой стрелке написаны в порядке возрастания числа от 1 до n, от 1 до m и от 1 до k соответственно. Стрелки зафиксировали таким образом, что когда стрелка первой оси указывает на число, стрелки двух других осей также указывают на числа. Витя записывает три числа (a1,a2,a3), на которые указывают стрелки. После этого он поворачивает первую шестеренку на угол 360°/n против часовой стрелки, чтобы напротив стрелки на первой оси оказался следующий (по часовой стрелке) зубец. При этом вторая шестеренка поворачивается на угол 360°/m по часовой стрелке (размеры зубцов у шестеренок одинаковые, поэтому размеры самих шестеренок разные, чтобы на границе шестеренок равномерно уложилось разное число одинаковых по размеру зубцов), а третья шестеренка поворачивается на угол 360°/k против часовой стрелки. Витя опять записывает три числа, на которые указывают стрелки.