Страница: << 1 2 3 4 5 6 7 >> Отображать по:
#860
Путь через горы
  
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
64 megabytes

Поверхность Земли в горной местности можно представить в виде ломаной линии. Вершины ломаной расположены в точках (x1, y1), (x2, y2),…,(xN, yN), при этом xi<xi+1.

Обычный горный маг находится в точке (x1, y1) и хочет попасть в точку (xN, yN). При этом он может перемещаться только пешком. Он может ходить по поверхности Земли (т.е. вдоль ломаной). А может сотворить в воздухе мост и пройти по нему. Мост может соединять две вершины ломаной: мост не может начинаться и заканчиваться не в вершине ломаной, и мост не может проходить под землей (в том числе не может быть туннелем в горе), но мост может каким-то своим участком проходить по поверхности земли. Длина моста не может быть больше R. Суммарно маг может построить не более K мостов.

Какое наименьшее расстояние придется пройти магу, чтобы оказаться в точке (xN, yN).

Входные данные

Вводится сначала натуральное число N (2≤N≤100). Затем водится натуральное число K (1≤K≤100) — максимальное количество мостов. Далее вводится целое число R (0≤R≤10000) — максимальная возможная длина моста. Далее вводятся координаты (x1, y1), (x2, y2),…,(xN, yN). Все координаты – целые числа, не превышающие по модулю 10000, для всех i от 1 до N–1: xi<xi+1.

Выходные данные

Выведите одно число — минимальную длину пути, которую придется пройти магу (как по земле, так и по мостам). Ответ выведите не менее чем с 5 цифрами после десятичной точки.

Примеры

Входных данные

Выходные данные

5 2 5

0 0

2 2

3 -1

4 1

5 0

6.47871

9 2 3

1 2

2 1

3 3

5 -1

6 2

7 0

8 1

9 0

10 1

14.93498
#1109
Мост
  
Источники: [ Командные олимпиады, ВКОШП, 2008, Задача B ]
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
256 megabytes

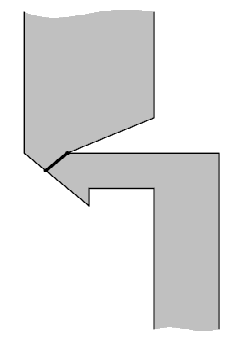
Власти Флатландии решили построить новый мост через реку Нижний Флат, протекающую с юга на север через территорию страны. В связи с финансовым кризисом средства строителей существенно ограничены, поэтому решено было построить мост минимальной возможной длины.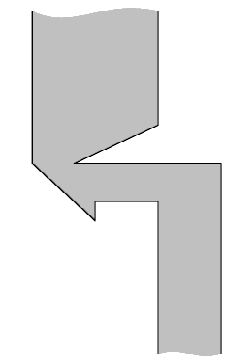

Введем координатную систему таким образом, чтобы ось OY была направлена с юга на север, а ось OX с запада на восток. Берега реки представляют собой ломаные, бесконечные в обе стороны. Левый берег начинается лучом, направленным на юг из точки (x1,1,y1,1), продолжается отрезками (x1,1,y1,1) − (x1,2,y1,2), (x1,2,y1,2)− (x1,3,y1,3), ..., (x1,m−1,y1,m−1) − (x1,m,y1,m) и заканчивается лучом, направленным на север из точки (x1,m,y,m).

Аналогично, правый берег реки начинается лучом, направленным на юг из точки (x2,1,y2,1), продолжается отрезками (x2,1,y2,1) − (x2,2,y2,2), (x2,2,y2,2) − (x2,3,y2,3), ..., (x2,n−1,y2,n−1) − (x2,n,y2,n) и заканчивается лучом, направленным на север из точки (x2,n,y2).

Помогите руководству Флатландии выяснить, мост какой минимальной длины можно построить.

Входные данные

Первая строка входного файла содержит целое число m (2 ≤ m ≤ 100). Следующие m строк содержат по два целых числа координаты вершин ломаной левого берега: x1,1, y1,1, x1,2,y1,2, ...,x1,m, y1,m.

Следующая строка входного файла содержит целое число n (2 ≤ n ≤ 100). Следующие n строк содержат по два целых числа координаты вершин ломаной правого берега: x2,1, y2,1, x2,2, y2,2, ..., x2,n, y2,n.

Известно, что x1,1 < x2,1, каждая из ломаных не имеет самопересечений и самокасаний, ломаные не имеют общих точек. Все отрезки каждой из ломаных имеют положительную длину. Все координаты не превосходят 104 по абсолютной величине

Выходные данные

Выведите в выходной файл одно вещественное число: минимальную возможную длину моста. Ваш ответ будет проверяться с точностью 10−5.

Оптимальное положение моста показано на следующем рисунке:


Примеры
Входные данные
4
6 1
3 1
3 0
0 3
3
9 3
2 3
6 5
Выходные данные
1.4142135623730951
#1128
Куда идем мы с Пяточком?
  
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes
На плоскости есть непроходимый круг. Необходимо найти кратчайший путь от точки до точки.

«Кто ходит в гости по утрам, тот поступает мудро…»

Пятачок и Винни-Пух каждое утро ходят пить чай в гости к Кролику. Естественно, самым коротким путем.

К сожалению, однажды Винни-Пуху пришла в голову идея вырыть ловушку для Слонопотама. Самое обидное, что они с Пятачком ее даже вырыли. Поэтому теперь каждое утро, идя в гости к Кролику, они боятся в нее провалиться.

Напишите программу, которая посчитает длину самого короткого безопасного пути от домика Винни-Пуха до домика Кролика.

Ловушка для Слонопотама представляет собой яму абсолютно круглой формы. Путь является безопасным, если он не проходит по ловушке (но может проходить по ее границе).

Входные данные

Во входном файле записаны сначала координаты домика Винни-Пуха XВ YВ, затем — координаты домика Кролика XК YК, а затем — координаты центра и радиус ловушки XЛ YЛ RЛ. Все координаты — целые числа из диапазона от –32000 до 32000. Радиус ловушки — натуральное число, не превышающее 32000.

Домики Винни-Пуха и Кролика не могут находиться внутри ловушки, но могут находиться на ее границе.

Выходные данные

Выведите в выходной файл одно число — длину самого короткого безопасного пути от домика Винни-Пуха до домика Кролика с тремя знаками после точки.

Примеры
Входные данные
0 0 10 0
5 5 1
Выходные данные
10.000
Входные данные
3 4 4 4
0 0 5
Выходные данные
1.000
#1134
РЛС
  
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes
Задана карта района, на которой присутствуют не более 5 связных фигур из клеток. Необходимо окружить все клетки забором минимальной длины (при этом группы клеток можно окружать отдельным забором).

Задачи противовоздушной обороны: ...борьба с десантом на всем маршруте пролета,

уничтожение вертолетов огневой поддержки, действующих из засады»

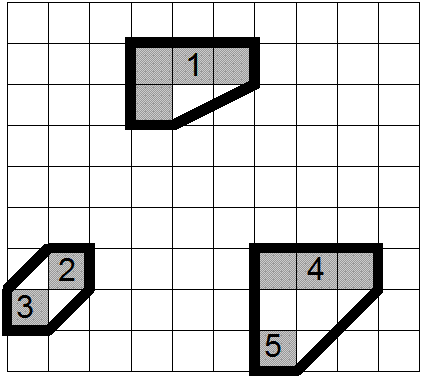Радиолокационная станция (РЛС) состоит из нескольких передатчиков (не более 5). К сожалению, их нельзя ставить рядом — они друг для друга создают помехи. Каждый передатчик состоит из квадратных модулей, которые располагаются вплотную друг к другу.

Вам дана карта района, в котором расположена РЛС. Вся карта для удобства разбита на квадраты, и для каждого квадрата известно, располагается в нем какой-то из модулей одного из передатчиков РЛС или нет.

Требуется оградить забором (или несколькими заборами) минимально возможной суммарной длины все передатчики РЛС. Забор — это произвольная ломаная (ее элементы не обязаны идти по сторонам клеток). Одним забором могут быть огорожены сразу несколько передатчиков.

Входные данные

Во входном файле записаны два числа N и M, задающие размеры района, в котором расположена РЛС (1N20, 1M20). Далее идет N строк, по M чисел в каждой, задающих карту района. Каждое из этих чисел 0 или 1 — 1 означает, что в этом квадрате находится один из модулей передатчика РЛС, а 0 — что в этом квадрате ничего ценного нет.

Общее количество передатчиков РЛС не превышает 5. Каждый передатчик — это связанная группа модулей (модули называются связанными, если они располагаются в квадратах карты, у которых есть общая граница, либо связаны через какие-то другие модули).

Ограничения на число модулей нет.

Выходные данные

В выходной файл выведите одно число — минимально возможную длину забора с тремя значащими цифрами после точки.

Примеры
Входные данные
2 2
1 0
0 1
Выходные данные
6.828
Входные данные
4 5
1 0 0 0 1
0 0 0 0 0
0 0 1 0 0
1 0 0 0 1
Выходные данные
18.000
#1189
Посчитайте лампы
  
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
64 megabytes

На новой станции метро, которую планируют открыть в конце этого года, будет N эскалаторов (эскалаторы пронумерованы подряд числами от 1 до N). Эскалаторы имеют длину L и расположены на расстоянии H друг от друга. Шириной эскалатором пренебрежем. Между каждыми двумя соседними эскалаторами (точно посередине) будет установлен ряд ламп. В ряду будет K ламп. Лампы устанавливаются по следующему принципу: всю длину эскалатора L разбивают на K равных отрезков и в середине каждого отрезка устанавливают по лампе (см. рисунок). Всего будет установлено (N–1)*K ламп.

На приведенном рисунке N=4 (эскалаторы показаны жирными <горизонтальными линиями), L=20, H=4, K=5.

Васе удалось проникнуть на эту станцию еще до ее открытия, и даже прокатиться на эскалаторе. Он выбрал эскалатор номер J. Посчитайте, в скольких точках эскалатора (включая его начало и конец) Вася будет видеть не все лампы (так как их будут загораживать другие лампы).

Входные данные

Во входном файле записаны числа N, L, H, K, J. Все числа — натуральные. 2≤N≤35, 1≤L≤1000, 1≤H≤1000, 1≤K≤35, 1≤J≤N.

Выходные данные

В выходной файл выведите одно число — ответ задачи.

Примеры
Входные данные
2 20 4 5 1
Выходные данные
0
Входные данные
4 20 4 5 2
Выходные данные
11
Страница: << 1 2 3 4 5 6 7 >> Отображать по:
Выбрано
:
Отменить
|
Добавить в контест