Петя любит ездить в школу на велосипеде. Но ездить на велосипеде по тротуарам запрещено, а ездить по дороге опасно. Поэтому Петя ездит только по специальным велосипедным дорожкам. К счастью, и Петин дом, и Петина школа находятся в непосредственной близости от таких дорожек.
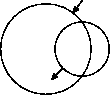
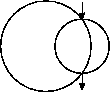
В городе, где живет Петя, есть ровно две велосипедных дорожки. Каждая дорожка имеет форму окружности. В точках их пересечения можно переехать с одной дорожки на другую.
Петя знает точку, в которой он заезжает на дорожку, и точку, в которой следует съехать, чтобы попасть в школу. Петю заинтересовал вопрос: какое минимальное расстояние ему следует проехать по дорожкам, чтобы попасть из дома в школу.
Будем считать, что в городе введена прямоугольная декартова система координат.
Первые две строки входных данных описывают велосипедные дорожки. Каждая из них содержит по три целых числа – координаты центра окружности, которую представляет собой соответствующая дорожка, и ее радиус. Координаты и радиус не превышают 200 по абсолютной величине, радиус – положительное число. Гарантируется, что дорожки не совпадают.
Следующие две строки содержат по два вещественных числа – координаты точки, где Петя заезжает на дорожку, и точки, в которой Петя съезжает с дорожки. Гарантируется, что каждая из точек с высокой точностью лежит на одной из дорожек (расстояние от точки до центра одной из окружностей отличается от ее радиуса не более, чем на 10-8). Точки могут лежать как на одной дорожке, так и на разных.
Выведите минимальное расстояние, которое следует проехать Пете по велосипедным дорожкам, чтобы попасть из дома в школу. Ответ должен отличаться от правильного не более, чем на 10-4.
Если доехать из дома до школы по велосипедным дорожкам невозможно, выведите число -1.
0 0 5 4 0 3 3.0 4.0 1.878679656440357 -2.121320343559643
8.4875540166
0 0 5 4 0 3 4.0 3.0 4.0 -3.0
6.4350110879
0 0 4 10 0 4 4.0 0.0 6.0 0.0
-1
Неудовлетворенный стандартным календарем своей операционной системы, Витя решил написать программу, которая будет выводить красиво отформатированный календарь. Он разработал формальные требования к календарю, но понял, что сам не способен написать соответствующую программу. Помогите ему.
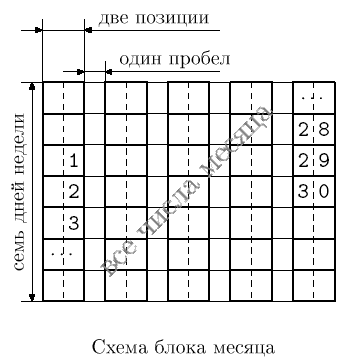
Календарь состоит из блоков, каждый из которых соответствует одному месяцу. Блоки расположены в виде таблицы из k столбцов и 12/k строк (k выбирается делителем числа 12). Месяцы выводятся в следующем порядке: первая строка содержит блоки, соответствующие месяцам с первого по k-ый, следующая – с (k + 1)-го по 2k-ый, и т. д.
Ширина всех блоков в столбце должна быть одинакова, высота всех блоков равна семи (числу дней в неделе). Между блоками различных строк таблицы выводится пустая строка, в каждой строке между соседними блоками из разных столбцов выводится три пробела.
Блок, соответствующий месяцу, устроен следующим образом. Каждой (в том числе неполной) неделе данного месяца в блоке соответствует столбец, имеющий ширину, равную двум. Между двумя соседними столбцами в каждой строке выводится один пробел. Если несколько блоков располагаются в одном столбце календаря, то для выравнивания ширины в те блоки, которые содержат меньше недель, в конец добавляется необходимое число пустых столбцов-недель. При этом разные столбцы календаря могут иметь разную ширину.
Все числа месяца заносятся в блок, соответствующий этому месяцу. Число заносится строку блока, соответствующую дню недели, на который приходится число в этом месяце. Число заносится в столбец блока, соответствующий неделе, к которой относится данное число. Однозначные числа дополняются слева одним пробелом. Таким образом, числа в столбце оказываются выравнены по правому краю.
 |  | |
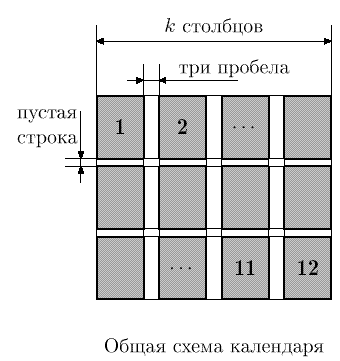| Общая схема календаря | Схема блока месяца |
На вход прораммы поступает описание года, календарь для которого следует вывести. Оно содержит три числа: d – день недели, на который приходится первое января ( 1
d7), l – является ли год високосным (l = 1 означает, что год является високосными, l = 0 – что не является) и k – количество столбцов в календаре (k – одно из чисел 1, 2, 3, 4, 6, 12).
Напомним, что високосный год отличается от обычного тем, что в високосном году февраль содержит 29 дней.
Выведите календарь, отформатированный в соответствии с условием задачи. Проверяющая программа в этой задаче игнорирует пробелы в конце строк. В остальном календарь должен быть отформатирован в точности так, как описано в условии.
4 1 4
5 12 19 26 2 9 16 23 1 8 15 22 29 5 12 19 26
6 13 20 27 3 10 17 24 2 9 16 23 30 6 13 20 27
7 14 21 28 4 11 18 25 3 10 17 24 31 7 14 21 28
1 8 15 22 29 5 12 19 26 4 11 18 25 1 8 15 22 29
2 9 16 23 30 6 13 20 27 5 12 19 26 2 9 16 23 30
3 10 17 24 31 7 14 21 28 6 13 20 27 3 10 17 24
4 11 18 25 1 8 15 22 29 7 14 21 28 4 11 18 25
3 10 17 24 31 7 14 21 28 5 12 19 26 2 9 16 23 30
4 11 18 25 1 8 15 22 29 6 13 20 27 3 10 17 24 31
5 12 19 26 2 9 16 23 30 7 14 21 28 4 11 18 25
6 13 20 27 3 10 17 24 1 8 15 22 29 5 12 19 26
7 14 21 28 4 11 18 25 2 9 16 23 30 6 13 20 27
1 8 15 22 29 5 12 19 26 3 10 17 24 31 7 14 21 28
2 9 16 23 30 6 13 20 27 4 11 18 25 1 8 15 22 29
6 13 20 27 4 11 18 25 1 8 15 22 29 6 13 20 27
7 14 21 28 5 12 19 26 2 9 16 23 30 7 14 21 28
1 8 15 22 29 6 13 20 27 3 10 17 24 1 8 15 22 29
2 9 16 23 30 7 14 21 28 4 11 18 25 2 9 16 23 30
3 10 17 24 1 8 15 22 29 5 12 19 26 3 10 17 24 31
4 11 18 25 2 9 16 23 30 6 13 20 27 4 11 18 25
5 12 19 26 3 10 17 24 31 7 14 21 28 5 12 19 26
В одном феодальном государстве средневековой Европы было n городов и m дорог, каждая из которых соединяла некоторые два города. Каждая дорога принадлежала правителю одного из городов (не обязательно одного из тех, которые она соединяла). Однажды правитель города S решил объявить войну правителю города T. Перед ним сразу же встала нелегкая задача: как довести армию до города T.
Правитель каждого города требует плату за проход войск через его город. Кроме того, правитель города S может перемещать войска только по дорогам, которые принадлежат ему. При этом он может купить любую дорогу у ее владельца за определенную плату (даже если владелец – правитель города T). К сожалению, все деньги из казны города S были потрачены на предыдущий неудачный военный поход, поэтому сначала правителю придется продать некоторые свои дороги (разумеется, после этого он не сможет провести по ним войска).
Помогите правителю выяснить, какие дороги следует продать, а какие купить, чтобы довести войска от города S до города T и оплатить проход через все промежуточные города. Все операции продажи и покупки дорог надо осуществить до начала похода, пока правители других городов не догадались о воинственных намерениях правителя города S.
В первой строке вводятся целые числа n и m – количество городов и дорог соответственно ( 2n2 000, 1m50 000). Города нумеруются от 1 до n, города S и T имеют номера 1 и n соответственно.
Следующие n строк содержат под одному целому числу ri – плату за проезд через город i ( 0ri10 000, r1 = rn = 0).
Далее идут m строк, задающих описания дорог. Дорога описывается четырьмя целыми числами: ai, bi, pi и ci. Здесь ai и bi – номера городов, которые соединяет дорога, pi – номер города, правителю которого она принадлежит, ci – ее стоимость ( ai
bi, 1ci10 000). По дороге можно перемещаться в обоих направлениях. Любые два города соединены не более, чем одной дорогой.
В первой строке выведите список дорог, которые нужно продать в следующем формате: сначала число дорог, а затем их номера. Дороги нумеруются с единицы в том порядке, в котором они заданы во входных данных. Во второй строке выведите список дорог, которые нужно купить, в том же формате. В третьей строке выведите маршрут похода – номера городов в порядке следования войска. Если решений несколько, выведите любое.
Если решения нет, выведите число -1.
3 3 0 1 0 1 2 1 10 2 3 1 10 3 1 2 2
2 1 2 1 3 1 3
Максимальное время работы на одном тесте: 2 секунды
Телевидение Флатландии готовится показать в вечернем эфире выступление одного известного политика. Поскольку политик известен своей несдержанностью, решено было написать специальную программу, которая вырезала бы из речи политика некоторые фразы, запуская в этот момент рекламу.
Поскольку ввести все неполиткорректные слова в программу представляется довольно сложным, решено было использовать эвристический алгоритм определения адекватности фразы.
Речь политика в реальном времени оцифровывается, распознается и подается на вход программе как последовательность фраз. Каждая фраза состоит из слов, записанных в одну строку. Слово представляет собой последовательность символов, ограниченную с обеих сторон границами фразы, пробелами или знаками препинания (символами «.», «!», «?», «:», «-», «,», «;», «(» или «)»).
Слово считается подозрительным, если в него входит не более трех различных букв (любой символ, кроме пробелов и знаков препинания считается буквой, большие и маленькие буквы считаются различными). Например, слова «дом», «мама» или «шалаш» являются подозрительными, а слова «привет», «Шалаш» или «hello» – нет.
Фраза считается подозрительной, если не менее половины слов в ней подозрительны (каждое вхождение слова во фразу считается отдельно).
Напишите программу, которая процензурирует речь политика, удалив из нее все подозрительные фразы.
Формат входных данных
Вводится не более 1000 фраз, каждая из которых представляет собой строку не длиннее 250 символов. Фраза содержит только символы с ASCII кодами от 32 до 255.
Формат выходных данных
Выведите все фразы из входных данных, которые не являются подозрительными. Фразы следует выводить в том же порядке, в котором они поступали на вход программы.
Примеры
| Входные данные | Выходные данные |
Наша система власти достаточно стабильна. | Наша система власти достаточно стабильна. |
Ваня очень любит шахматы. Причем он не только любит просто играть в шахматы, но часто придумывает разные головоломки и просто забавные задачки с использованием шахматных фигур. Также вместо стандартной шахматной доски 8×8 Ваня часто использует в своих задачах доски другого размера.
Недавно он придумал новую головоломку и рассказал ее своим друзьям. Суть головоломки заключается в следующем. На одно из полей доски размером m×n записывается некоторое положительное целое число и затем на него ставится ферзь.
После этого Ваня делает k ходов ферзем, каждый раз перемещая его по шахматным правилам на одно из полей, на котором он еще не был. При этом каждый раз, перед тем как поставить ферзя на некоторое поле, он записывает на это поле целое число, причем это число всегда больше всех чисел, уже записанных на доске.
Задача друзей Вани – по числам, записанным на доске, восстановить маршрут ферзя или выяснить, что Ваня где-то ошибся. Поскольку Ваня часто выбирает достаточно большие m, n и k, друзья устали решать эту головоломку вручную и решили написать для ее решения программу. Помогите им
Напомним, что по шахматным правилам ферзь может пойти на любое поле доски, находящееся на одной вертикали, горизонтали или диагонали с тем полем, на котором он находится.
В первой строке вводятся числа m, n и k ( 1m, n300, 0k < mn). Следующие m строк содержат по n целых чисел и описывают поля доски (пустому полю соответствует число 0, а полю, на котором записано число – это число). Все числа, записанные на доске, положительные, целые и не превышают 109.
Если Ваня ошибся при построении головоломки, выведите сообщение «Wrong Board».
В противном случае выведите m строк по n чисел – для каждого поля выведите номер хода, перед которым ферзь побывал на этом поле, а для последнего поля, на котором он оказался – число k + 1. Для полей, на которые ферзь не попадал, выведите число 0.
4 4 7 10 20 0 100 30 0 0 40 0 0 0 0 45 42 0 70
1 2 0 8 3 0 0 4 0 0 0 0 6 5 0 7
2 4 4 10 20 30 40 0 50 0 0
Wrong Board
2 2 2 1 2 4 3
Wrong Board