Темы --> Информатика
    Язык программирования(952 задач)
    Алгоритмы(1657 задач)
    Структуры данных(279 задач)
    Интерактивные задачи(17 задач)
    Другое(54 задач)
---> 110 задач <---
Источники --> Командные олимпиады --> ВКОШП
    1999(7 задач)
    2000(8 задач)
    2001(8 задач)
    2002(9 задач)
    2003(9 задач)
    2004(10 задач)
    2005(10 задач)
    2006(10 задач)
    2007(11 задач)
    2008(10 задач)
    2009(11 задач)
    2010(11 задач)
    2011(11 задач)
    2012(11 задач)
    2013(11 задач)
    2014(11 задач)
    2015(11 задач)
    2016(11 задач)
Страница: << 12 13 14 15 16 17 18 >> Отображать по:
#587
Симпатичные узоры
  
Источники: [ Командные олимпиады, ВКОШП, 2000, Задача E ]
Прямоугольное поле заполнено белыми и черными клетками, требуется определить количество вариантов замощения поля таким образом, чтобы на нем не встречалось ни одного белого или черного квадрата 2 на 2.

Компания BrokenTiles планирует заняться выкладыванием во дворах у состоятельных клиентов узор из черных и белых плиток, каждая из которых имеет размер 1×1 метр. Известно, что дворы всех состоятельных людей имеют наиболее модную на сегодня форму прямоугольника M×N метров.

Однако при составлении финансового плана у директора этой организации появилось целых две серьезных проблемы: во первых, каждый новый клиент очевидно захочет, чтобы узор, выложенный у него во дворе, отличался от узоров всех остальных клиентов этой фирмы, а во вторых, этот узор должен быть симпатичным.

Как показало исследование, узор является симпатичным, если в нем нигде не встречается квадрата 2×2 метра, полностью покрытого плитками одного цвета. На рисунке 1 показаны примеры различных симпатичных узоров, а на рисунке 2 - несимпатичных.

Для составления финансового плана директору необходимо узнать, сколько клиентов он сможет обслужить, прежде чем симпатичные узоры данного размера закончатся. Помогите ему!

Входные данные

В первой строке входных данных содержатся два положительных целых числа, разделенных пробелом: \(M\) и \(N\) (1 <= \(M\)·\(N\) <= 30).

Выходные данные

Выведите единственное число - количество различных симпатичных узоров, которые можно выложить во дворе размера \(M\)×\(N\) . Узоры, получающиеся друг из друга сдвигом, поворотом или отражением, считаются различными.

Примеры
Входные данные
1 2
Выходные данные
4
Входные данные
4 1
Выходные данные
16
#588
Кубики
  
Источники: [ Командные олимпиады, ВКОШП, 2000, Задача F ]
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
64 megabytes
Даны кубики с 6 буквами написанными на них и слово. Требуется составить слово из кубиков.

Родители подарили Пете набор детских кубиков. Поскольку Петя скоро пойдет в школу, они купили ему кубики с буквами. На каждой из шести граней каждого кубика написана буква.

Теперь Петя хочет похвастаться перед старшей сестрой, что научился читать. Для этого он хочет сложить из кубиков ее имя. Но это оказалось довольно сложно сделать - ведь разные буквы могут находиться на одном и том же кубике и тогда Петя не сможет использовать обе буквы в слове. Правда одна и та же буква может встречаться на разных кубиках. Помогите Пете!

Дан набор кубиков и имя сестры. Выясните, можно ли выложить ее имя с помощью этих кубиков и если да, то в каком порядке следует выложить кубики.

Входные данные

В первой строке вводится число \(N\) (1 <= \(N\) <= 100) - количество кубиков в наборе у Пети. Во второй строке задано имя Петиной сестры - слово, состоящие только из больших латинских букв, не длиннее 100 символов. Следующие N строк содержат по 6 букв (только большие латинские буквы), которые написаны на соответствующем кубике.

Выходные данные

В первой строке выведите "YES" если выложить имя Петиной сестры данными кубиками можно, "NO" в противном случае.

В случае положительного ответа, во второй строке выведите \(M\) различных чисел из диапазона 1…\(N\), где \(M\) - количество букв в имени Петиной сестры. \(i\)-е число должно быть номером кубика, который следует положить на \(i\)-е место при составлении имени Петиной сестры. Кубики нумеруются с 1, в том порядке, в котором они заданы во входных данных. Если решений несколько, выведите любое. Разделяйте числа пробелами.

Примеры
Входные данные
2
AB
AAAAAB
AAAAAA
Выходные данные
YES
2 1
Входные данные
3
ANNY
AAAAAA
NNNNNN
YYYYYY
Выходные данные
NO
#590
Похожие матрицы
  
Источники: [ Командные олимпиады, ВКОШП, 2000, Задача H ]
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
64 megabytes
Необходимо по данной матрице построить матрицу, у которой сумма строк и столбцов совпадает с суммами исходной матрицы, все числа кратны заданному P, а также отличаются от соответствующих чисел исходной матрице не более, чем на P.

Рассмотрим таблицу, состоящую из \(N\) строк и \(M\) столбцов. Если в каждой ячейке такой таблицы стоит целое число, назовем такую таблицу целочисленной матрицей. Скажем, что эта матрица кратна чиcлу \(p\), если все числа в ее ячейках кратны \(p\).

Рассмотрим теперь суммы элементов матрицы по строкам и столбцам соответственно. Обозначим сумму чисел \(i\)-й строки за \(H_i\), а сумму чисел \(j\)-го столбца за \(V_j\). Упорядоченный набор чисел (\(H_1\), \(H_2\), …, \(H_N\), \(V_1\), \(V_2\), …, \(V_M\)) назовем профилем матрицы. Скажем, что матрица почти кратна \(p\), если все числа, входящие в ее профиль, кратны \(p\). Почти кратная 5 матрица и ее профиль изображены на рисунке 1.

Если две матрицы \(A\) и \(B\) имеют одинаковый размер, причем элемент, стоящий на пересечении \(i\)-й строки и \(j\)-го столбца в матрице \(A\) отличается от соответствующего элемента матрицы \(B\) не более чем на \(p\), скажем, что \(A\) отличается от \(B\) не более чем на \(p\). Скажем, что матрица \(B\) похожа на матрицу \(A\) относительно числа \(p\), если
1. отличается от не более чем на \(p\)
2. профили \(B\) и \(A\) совпадают.
На рисунке 2 изображены две похожие относительно числа 5 матрицы, первая из них почти кратна 5, а вторая кратна 5. Третья матрица на рисунке 2 тоже кратна 5, но непохожа на первую (хотя похожа на вторую).

Дано число p и почти кратная p матрица A. Ваша задача - найти такую матрицу B, чтобы она была кратна p и похожа на A относительно p.

Входные данные

В первой строке входных данных задаются целые числа \(p\) (1 <= \(p\) <= 10), \(N\) и \(M\) (1 <= \(N\), \(M\) <= 30). Следующие \(N\) строк содержат по \(M\) целых неотрицательных чисел, не превышающих 1000, которые являются элементами исходной матрицы \(A\).

Выходные данные

Выведите матрицу \(B\) по строкам - сначала \(M\) элементов первой строки, затем \(M\) элементов второй, и т. д. Разделяйте числа пробелами и/или переводами строк. Заботиться о красивом форматировании таблицы не надо. Если искомой матрицы не существует, выведите единственное число - "-1". Если решений несколько, выведите любое из них.

Примеры
Входные данные
3 3 3
1 2 3
2 3 1
3 1 2
Выходные данные
3 0 3 
0 3 3 
3 3 0
#1108
Место у прохода, пожалуйста
  
Источники: [ Командные олимпиады, ВКОШП, 2008, Задача A ]
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
256 megabytes

Те, кто часто путешествуют самолетами, любят просить место у прохода. Ведь если сидеть у прохода, можно встать и прогуляться, не тревожа своих соседей.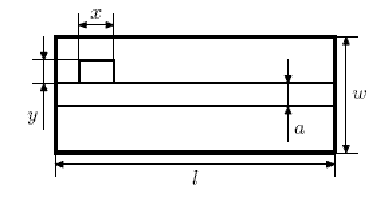

Компания «Аэротрам» готовит к производству новый самолет «T-239-n». Перед инженерами встала задача спланировать организацию салона, чтобы как можно больше мест было у прохода. Будем использовать следующую упрощенную математическую модель салона самолета. В горизонтальном сечении салон представляет собой прямоугольник длиной l и шириной w сантиметров. Кресло представляет собой прямоугольник размером x на y сантиметров и должно быть расположено в салоне так, чтобы его сторона длиной x была параллельна стороне салона длиной l. Проход представляет собой полосу шириной a, параллельную стороне салона длиной l. Проход идет вдоль всего салона.

В салоне требуется разместить n кресел. Помогите инженерам компании выяснить, как организовать салон, чтобы максимальное количество кресел было расположено у прохода. В салоне необходимо сделать хотя бы один проход. Кресло считается расположенным у прохода, если оно имеет хотя бы одну общую сторону с проходом.

Входные данные

Входной файл содержит шесть целых чисел: n, l, w, x, y и a (1 ≤ n ≤ 10000, 1 ≤ l,w,x,y,a ≤ 104).

Выходные данные

Если разместить n кресел в салоне так, чтобы был хотя бы один проход, невозможно, выведите в выходной файл единственное число −1 . Иначе выведите максимальное количество кресел, которое можно разместить у прохода.

Комментарий к примерам тестов.

В первом примере оптимально расположить кресла, например, следующим образом:


Примеры
Входные данные
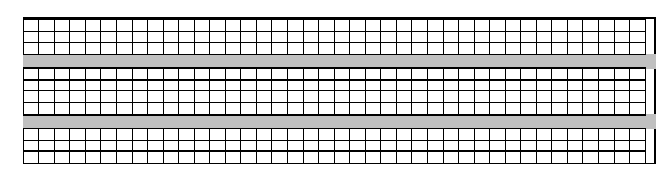
400 3250 750 80 60 70
Выходные данные
160
Входные данные
450 3250 750 80 60 70
Выходные данные
-1
#1109
Мост
  
Источники: [ Командные олимпиады, ВКОШП, 2008, Задача B ]
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
256 megabytes

Власти Флатландии решили построить новый мост через реку Нижний Флат, протекающую с юга на север через территорию страны. В связи с финансовым кризисом средства строителей существенно ограничены, поэтому решено было построить мост минимальной возможной длины.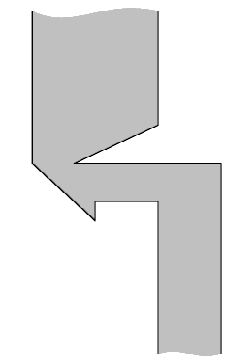

Введем координатную систему таким образом, чтобы ось OY была направлена с юга на север, а ось OX с запада на восток. Берега реки представляют собой ломаные, бесконечные в обе стороны. Левый берег начинается лучом, направленным на юг из точки (x1,1,y1,1), продолжается отрезками (x1,1,y1,1) − (x1,2,y1,2), (x1,2,y1,2)− (x1,3,y1,3), ..., (x1,m−1,y1,m−1) − (x1,m,y1,m) и заканчивается лучом, направленным на север из точки (x1,m,y,m).

Аналогично, правый берег реки начинается лучом, направленным на юг из точки (x2,1,y2,1), продолжается отрезками (x2,1,y2,1) − (x2,2,y2,2), (x2,2,y2,2) − (x2,3,y2,3), ..., (x2,n−1,y2,n−1) − (x2,n,y2,n) и заканчивается лучом, направленным на север из точки (x2,n,y2).

Помогите руководству Флатландии выяснить, мост какой минимальной длины можно построить.

Входные данные

Первая строка входного файла содержит целое число m (2 ≤ m ≤ 100). Следующие m строк содержат по два целых числа координаты вершин ломаной левого берега: x1,1, y1,1, x1,2,y1,2, ...,x1,m, y1,m.

Следующая строка входного файла содержит целое число n (2 ≤ n ≤ 100). Следующие n строк содержат по два целых числа координаты вершин ломаной правого берега: x2,1, y2,1, x2,2, y2,2, ..., x2,n, y2,n.

Известно, что x1,1 < x2,1, каждая из ломаных не имеет самопересечений и самокасаний, ломаные не имеют общих точек. Все отрезки каждой из ломаных имеют положительную длину. Все координаты не превосходят 104 по абсолютной величине

Выходные данные

Выведите в выходной файл одно вещественное число: минимальную возможную длину моста. Ваш ответ будет проверяться с точностью 10−5.

Оптимальное положение моста показано на следующем рисунке:


Примеры
Входные данные
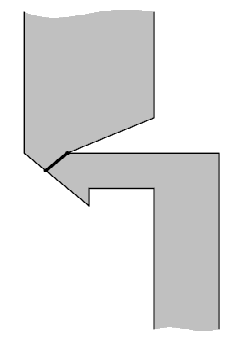
4
6 1
3 1
3 0
0 3
3
9 3
2 3
6 5
Выходные данные
1.4142135623730951
Страница: << 12 13 14 15 16 17 18 >> Отображать по:
Выбрано
:
Отменить
|
Добавить в контест