Baltic Olympiad in Informatics 2017(0 задач)
Baltic Olympiad in Informatics 2016(6 задач)
Baltic Olympiad in Informatics 2015(0 задач)
Baltic Olympiad in Informatics 2014(2 задач)
Baltic Olympiad in Informatics 2013(1 задач)
Компания сотрудников должна провести реструктуризацию. В результирующей иерархии, представленной как корневое дерево, каждый узел будет боссом своих детей. Кроме того, всем работникам должна быть назначена зарплата. Зарплата должна быть положительным целым числом, а зарплата каждого босса должна быть больше суммы окладов их непосредственных подчиненных. Ваша задача состоит в том, чтобы структурировать компанию, чтобы все вышеперечисленные условия соблюдались, а сумма всех зарплат была как можно меньше.
Первая строка ввода содержит целое число: количество сотрудников. Сотрудники имеют номера от 1 до n . После этого вход содержит n строк, описывающих предпочтения сотрудников. В i -й строке содержится целое число k i , за которым следует список целых чисел. Список состоит из всех сотрудников, которых i -й работник готов принять в качестве своего босса.
Вы должны получить самую низкую общую зарплату среди всех действительных реструктуризаций. Гарантируется что существует хотя бы одно решение.
подзадача 1(22 балла)
2 < n < 10 k i ≤ 20
подзадача 2(45 балла)
2 <
n
< 100
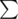 k
i
≤ 200
k
i
≤ 200
подзадача 3(33 балла)
2 <
n
< 5000
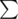 k
i
≤ 10000
k
i
≤ 10000
4 1 4 3 1 3 4 2 1 2 1 3
8
В столице города Бестеланд есть огороженный парк, площадь которого представляет собой прямоугольник. Деревья и посетители в парке представляют собой круги. В парке есть четыре входа, по одному в каждом углу (1 = внизу слева, 2 = внизу справа, 3 = верхний правый, 4 = верхний левый). Посетители могут войти и выйти из парка только через входы. Посетители могут войти и выйти из парка, когда они касаются обеих сторон угла соответствующего входа. Посетители могут свободно передвигаться по парку, но они не могут пересекаться ни с деревьями, ни с забором. Ваша задача для каждого посетителя, учитывая вход, через который он войдет в парк, рассчитать через какие входы он может выйти из парка.
Первая строка ввода содержит два целых числа n и m : число деревьев в парке и количество посетителей. Вторая строка ввода содержит два целых числа w и h : ширину и высоту парковой зоны. Левый нижний угол имеет координаты(0, 0), верхний правый угол имеет координаты ( w , h ) . следующие строки описывают деревья. Каждая строка содержит три целых числа x , y и r : координаты центра дерева ( x , y ) и его радиус r . Деревья не перекрывают друг друга или забор. Наконец, есть m строк, которые описывают посетителей. Каждая строка содержит два целых числа r и e: радиус посетителя, и вход, который они войдут в парк. Кроме того, ни одно дерево не перекрывает квадратную площадь в каждом углу, где находится радиус наибольшего посетителя.
Вы должны вывести для каждого посетителя одну строку, содержащую входы, через которые посетитель может выйти из парка, в отсортированном порядке без пробелов между ними.
Два объекта касаются, если они имеют одну общую точку. Два объекта перекрываются, если они имеют более одной общей точки
4 k < w , h < 10 9 где k - радиус самого большого дерева
подзадача 1(27 баллов)
1 < = n < = 2000
m = 1
подзадача 2(31 балл)
1 < = n < = 200
1 < = m < = 10 5
подзадача 3(42 балл)
1 < = n < = 2000
1 < = m < = 10 5
5 3 16 11 11 8 1 6 10 1 7 3 2 10 4 1 15 5 1 1 1 2 2 2 1
1234 2 14
Сетка размера (2 n + 1) * (2 n + 1) была построена следующим образом. Номер 1 был помещен в центральный квадрат, номер 2 был помещен справа от него, а следующие числа были помещены вдоль спирали против часовой стрелки.
Ваша задача - рассчитать ответы на q запросов, где запрашивается сумма чисел в прямоугольной области в сетке (по модулю 10 9 + 7 ). Например, в следующей сетке n = 2 а сумма чисел в серой области 74 :
Первая строка ввода содержит два целых числа n и q : размер сетки и количество запросов.
дальше идут q строк, каждая из которых содержит четыре целых числа x 1 , y 1 , x 2 , y 2 , ( - n ≤ x 1 ≤ x 2 ≤ n , - n ≤ y 1 ≤ y 2 ≤ n , ) . Вы должны рассчитать сумму чисел в прямоугольной области с углами ( x 1 , y 1 ) и ( x 2 , y 2 ) .
Вы должны вывести ответ для каждого запроса (по модулю 10 9 + 7 ).
Во всех тестах 1 ≤ q ≤ 100
Подгруппа 1(12 баллов)
1 ≤ n ≤ 1000
Подгруппа 2(15 баллов)
1 ≤ n ≤ 10 9
x 1 = x 2 и y 1 = y 2
Подгруппа 3(17 баллов)
1 ≤ n ≤ 10 5
Подгруппа 4(31 балл)
1 ≤ n ≤ 10 9
x 1 = y 1 = 1
Подгруппа 5(25 балл)
1 ≤ n ≤ 10 9

2 3 0 -2 1 1 -1 0 1 0 1 2 1 2
74 9 14
Есть n городов в Байтландии, и k из них важные города, часто посещаемые королем. В стране есть m дорог, каждая из которых соединяет два города. К сожалению, состояние дорог настолько плохо, что король не может проехать через них с полной скоростью на своих спортивных автомобилях. Для каждой дороги известны затраты на ее обновление. Ваша задача - выбрать, какие дороги будут отремонтированы, чтобы все k важных города были связаны отремонтированными дорогами, а общая стоимость была как можно ниже.
Первая строка ввода содержит три целых числа n , k и m : количество городов, количество важных городов и количество дорог. Города пронумерованы 1, 2, ..., n . Вторая строка ввода содержит k целых чисел: важные города.
Следующие m строк, описывают дороги. Каждая строка содержит три целых числа a , b и c , что означает, что существует двунаправленная дорога между городами a и b , а стоимость ремонта дороги - c .
Гарантируется, что существует маршрут между любыми двумя городами.
Вы должны вывести минимальные затраты на ремонт дорог, чтобы король мог путешествовать между всеми важными городами на своих спортивных автомобилях.
Во всех тестах 1 ≤ c ≤ 10 9 и n ≥ k
Подгруппа 1 (22 баллов)
2 ≤ k ≤ 5
n ≤ 20
1 ≤ m ≤ 40
Подгруппа 2 (14 баллов)
2 ≤ k ≤ 3
n ≤ 10 5
1 ≤ m ≤ 2 * 10 5
Подгруппа 3 (15 баллов)
2 ≤ k ≤ 4
n ≤ 1000
1 ≤ m ≤ 2000
Подгруппа 4 (23 баллов)
k = 4
n ≤ 10 5
1 ≤ m ≤ 2 * 10 5
Подгруппа 5 (26 баллов)
k = 5
n ≤ 10 5
1 ≤ m ≤ 2 * 10 5
4 3 6 1 3 4 1 2 4 1 3 9 1 4 6 2 3 2 2 4 5 3 4 8
11
Вам предоставляется последовательность из n чисел x 1 , x 2 , ..., x n . Каждое число 1, 2, ..., n появляется ровно один раз в последовательности.
Вы можете изменить последовательность с помощью свопов. Существует n - 1 последовательных "поворотов" пронумерованных k = 2, 3, ..., n . При "повороте" k вы можете либо менять значения x k и x ⌊ k / 2⌋ в последовательности, либо ничего не делать.
Последовательность a 1 , a 2 , ..., a n лексикографически меньше, чем последовательность b 1 , b 2 , ..., b n , если существует индекс j (1 ≤ j ≤ n ) такой, что a k = b k для всех k < j и a j < b j .
Какова минимальная лексикографическая последовательность, которую вы можете получить?
Первая строка ввода содержит целое число n.
Вторая строка ввода содержит n целых чисел: числа в последовательности.
Вы должны вывести n целых чисел: лексикографически минимальную последовательность.
Подгруппа 1(10 баллов)
1 ≤ n ≤ 20
Подгруппа 2(11 баллов)
1 ≤ n ≤ 40
Подгруппа 3(27 баллов)
1 ≤ n ≤ 1000
Подгруппа 4(20 баллов)
1 ≤ n ≤ 5 * 10 4
Подгруппа 5(32 балла)
1 ≤ n ≤ 2 * 10 5
5 3 4 2 5 1
2 1 3 4 5