--->
16 задач
<---
Источники
ограничение по времени на тест
4.0 second;
ограничение по памяти на тест
256 megabytes
Рассмотрим следующую игру об удалении вершин из графа, представляющего лес (то есть объединение нескольких деревьев). Изначально граф состоит из одного дерева из n вершин, а количество очков равно 0 .
Игра задаётся перестановкой вершин и происходит следующим образом:
- Если граф опустел, то игра заканчивается.
- Иначе выбирается первая ещё не удалённая вершина в перестановке, после чего
- Количество очков увеличивается на размер дерева из которого была выбрана вершина, а затем выбранная вершина и все связанные с ней рёбра удаляются, и тот же процесс продолжается на оставшемся графе.
Просуммируем число очков по всем возможным n ! играм. Выведите это число по модулю 10 9 + 7 .
Входные данные
В первой строке входного файла дано число N ( 2 ≤ n ≤ 10 5 ) — количество вершин в исходном дереве.
Каждая из последующих N - 1 строк содержит два числа — x i , y i задающих концы соответствующего ребра дерева ( 1 ≤ x i , y i ≤ n ).
Выходные данные
Выведите одно число — суммарное количество очков по модулю 10 9 + 7 .
Система оценки
Тесты к данной задаче состоят из 3 групп:
- (20 баллов) n ≤ 10 .
- (40 баллов) n ≤ 5000
- (40 баллов) n ≤ 10 5
Примеры
Входные данные
2 1 2
Выходные данные
6
Входные данные
3 1 2 2 3
Выходные данные
34
#113866
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes
Мирко стал генеральным директором крупной корпорации. В компании работает N человек, пронумерованных от 1 до N , Мирко имеет номер 1 . У всех кроме Мирко есть начальник. Начальник может иметь несколько подчинённых, но не более одного своего начальника.
Когда Мирко получает задание от инвесторов, он передаёт его своему подчинённому с наименьшим номером. Этот подчинённый также передаёт его своему подчинённому с наименьшим номером, и так далее, пока задание не перейдёт несчастливому работнику без подчинённых, который должен сделать задание.
Этот работник получает 1 монету, его начальник получает 2 монеты, начальник этого начальника получает 3 и так далее. Потом тот, кто на самом деле сделал работу, осознаёт, насколько эта капиталистическая система несправедлива и увольняется с работы.
Мирко получает задания до тех пор, пока в корпорации не останется всего один сотрудник — сам Мирко. Тогда он выполняет это задание, получает 1 монету и уходит из корпорации. Ему стало интересно, сколько всего монет получил каждый бывший сотрудник. Помогите ему с этим.
Входные данные
Первая строка содержит одно натуральное число N ( 1 ≤ N ≤ 2·10 5 ) — число сотрудников компании. Следующая строка содержит N - 1 чисел a 2 , a 3 , ... a n ( 1 ≤ a i < i ), a i — номер начальника i -го сотрудника.
Выходные данные
Выведите N чисел, i -е число должно означать, сколько монет получил i -й сотрудник
Система оценки
Программы, верно работающие при 2 ≤ N ≤ 5000 оцениваются в 50 баллов.
Примечание
Пояснения к первому примеру:
Примеры
Входные данные
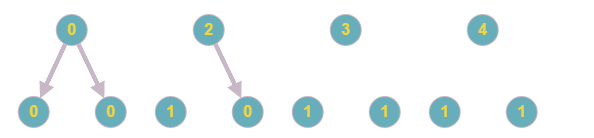
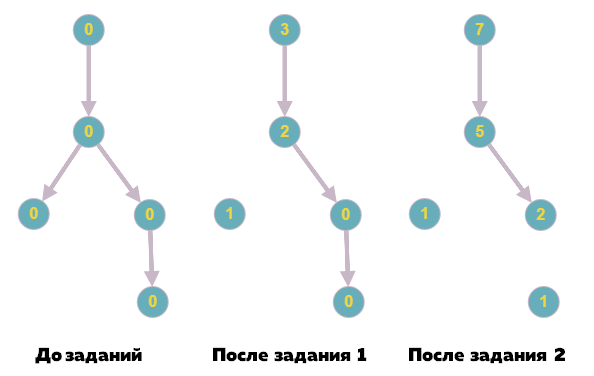
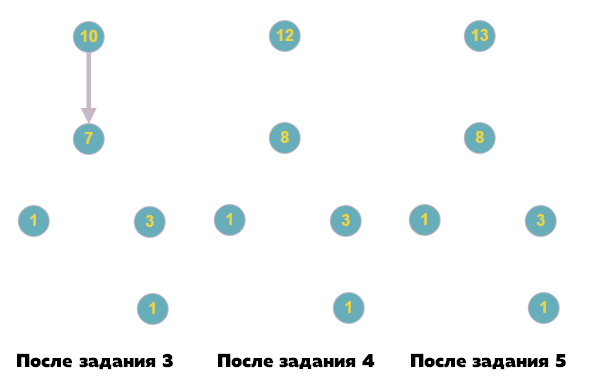
3 1 1
Выходные данные
5 1 1
Входные данные
5 1 2 2 4
Выходные данные
13 8 1 3 1
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
512 megabytes
В двусвязном списке, он же LinkedList, каждый элемент может быть связан максимум с двумя другими элементами — с предыдущим элементом (если он есть) и со следующим элементом (если он есть).
Билли и Рикардо проходят стажировку в компании FlexDex в группе поддержки внутреннего анонимного форума с возможностью деанонимизации. Для представления последовательных сообщений в теме необходимо использовать список, где элементами будут являться эти сообщения, и два товарища решили написать свою быструю реализацию двусвязного списка FlexList.
Но у них что-то пошло не так — в их списке новое сообщение может связываться не только с первым или последним сообщением, как должно быть, а с любым из уже существующих сообщений.
Если представить каждое сообщение как вершину графа, а связи между сообщениями как ребра графа, то гарантируется, что этот граф будет неориентированным, связным и ацикличным.
Говорится, что граф является корректным графом, если в этом графе у каждой вершины не более двух вершин, связанных с ней ребром. Изначально же FlexList связи между сообщениями могут выглядеть в виде любого связного ацикличного графа, не обязательно корректного.
Билли и Рикардо не растерялись и решили, что будут вручную исправлять все неясности в ходе работы программ, которые используют их изобретение. Тимлид дал им тестовый пример для проверки кода. Они получили на этом примере граф связей и вручную делают из него корректный граф, ведь связи между сообщениями в корректном двусвязном списке могут представлять собой только корректный граф.
Это выглядит так — сначала Билли проверяет, что граф корректный. Если это не так, то он выбирает и удаляет некоторый лист (вершина, у которой есть ровно одна связь с другими вершинами), и отдает граф Рикардо, затем Рикардо делает то же самое и отдает граф Билли, и так продолжается до тех пор, пока кто-то не получит от товарища корректный граф. Как только один из двух друзей получает такой граф, то тут же показывает его тимлиду, с надеждой на похвалу и повышение в должности.
Каждый хочет получить первым такой граф. Кто первым попадет к тимлиду, если оба товарища удаляют листья оптимально для себя?
Входные данные
В первой строке содержится одно целое число \(n\) (\(1 \leq n \leq 300\,000\)) — число сообщений в примере тимлида. Следующие \(n - 1\) строк задают связи между сообщениями. Каждая из них содержит два целых числа \(a_i\) и \(b_i\) (\(1 \leq a_i, b_i \leq n\), \(a_i \neq b_i\)), которые показывают, что сообщения с номерами \(a_i\) и \(b_i\) связаны.
Выходные данные
Выведите "Billy" (без кавычек), если первым попадет к тимлиду Билли, иначе выведите "Ricardo" (без кавычек).
Примечание
В первом примере Билли первым ходом может удалить одну из вершин с номерами \(2\), \(4\) или \(5\), так как они являются листьями. Он не будет удалять вершину с номером \(4\) или \(5\), так как в таком случае он передаст Рикардо корректный граф и проиграет. Значит, он удалит вершину \(2\). В свою очередь, Рикардо может удалить вершины \(1\), \(4\) или \(5\), и, в любом случае, Билли получит от него корректный граф.
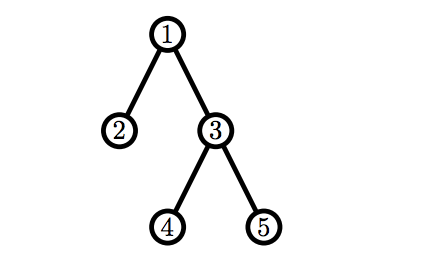
Во втором примере у Билли сразу есть корректный граф.
В третьем примере можно показать, что вне зависимости от ходов Билли, Рикардо получит корректный граф первым.
Примеры
Входные данные
5 1 2 1 3 3 4 3 5
Выходные данные
Billy
Входные данные
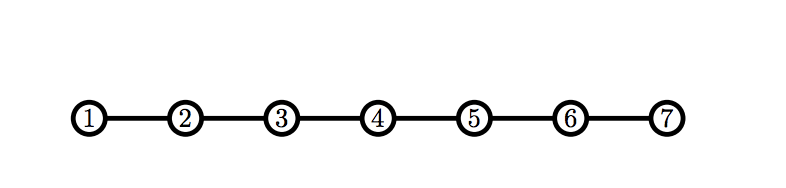
7 1 2 2 3 3 4 4 5 5 6 6 7
Выходные данные
Billy
Входные данные
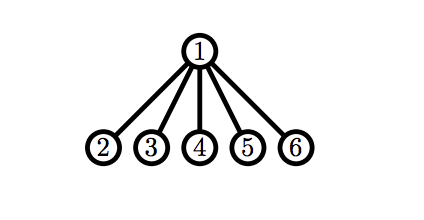
6 1 2 1 3 1 4 1 5 1 6
Выходные данные
Ricardo
У Аркадия в саду есть одна необычная яблоня, с которой иногда необходимо собирать яблоки. Так как яблоня необычная, на ней есть \(n\) соцветий, они пронумерованы от 1 до \(n\). Соцветие номер 1 находится около корня дерева, любое другое соцветие с номером \(i(i>1)\) расположено на верхнем конце ветки, нижний конец которой расположен в соцветии \(p_i\).
Когда яблоки созревают, одновременно появляется ровно по одному яблоку в каждом соцветии. В тот же момент все яблоки начинают скатываться вниз по веткам к корню дерева. Каждую секунду все яблоки, кроме находящегося в первом соцветии, одновременно скатываются на одну ветку ближе к корню, то есть, например, из соцветия a яблоко попадет в соцветие \(p_a\). Яблоки, находившиеся в первом соцветии, забирает Аркадий. Яблоня необычная, поэтому, если в какой-то момент в одном соцветии оказываются два яблока, они аннигилируют. Так происходит с каждой парой, например, если в соцветие попадет одновременно 5 яблок, то останется только одно яблоко, а если в соцветие попадет одновременно 8 яблок, то не останется ни одного яблока. Таким образом, в каждом соцветии в любой момент времени находится не более одного яблока.
Помогите Аркадию, подсчитайте, сколько яблок он сможет забрать из первого соцветия за один урожай.
Входные данные
В первой строке следует целое число \(n(2 \le n \le 100000)\) — количество соцветий.
Во второй строке следует последовательность целых чисел \(p_2, p_3, ..., p_n\), состоящая из \(n−1\) числа, где \(p_i\) равно номеру соцветия, в которое скатывается яблоко из соцветия \(i\).
Выходные данные
Выведите количество яблок, которые Аркадий сможет забрать из первого соцветия за один урожай.
Примеры
Входные данные
3 1 2
Выходные данные
3
Входные данные
5 4 2 5 1
Выходные данные
5
#114325
ограничение по времени на тест
0.5 second;
ограничение по памяти на тест
256 megabytes
Мислав и Мирко разработали новую игру под названием повороты.
Сначала Мирко выбирает последовательность чисел длины \(n\) и число \(k\) и разбивает последовательность на секции, каждая из которых содержит \(k\) чисел (\(n\) делится на \(k\)). Первая секция содержит первые \(k\) позиций в последовательности, вторая секция содержит последующие \(k\) позиций в последовательности и так далее.
После этого Мирко начинает применять различные операции на данной последовательности. Есть два типа операций:
1. Совершить циклический сдвиг элементов последовательности чисел в каждой секции на \(x\) влево или вправо.
2. Совершить циклический сдвиг элементов последовательности чисел целиком на \(x\) влево или вправо.
Заметим, что операция типа 2 может изменить то, к какой секции принадлежит какое число.
После применения всех операций, Мирко сообщает Миславу получившуюся последовательность и применённые операции. Задача Мислава заключается в том, чтобы восстановить исходную последовательность. Он попросил вас о помощи.
Входные данные
Первая строка ввода содержит три целых числа \(n\), \(k\), \(q\) (\(1 \le n \le 100000; 1 \le k \le 100000; 1 \le q \le 100000\)) - длину последовательности, длину каждой секции и количество применённых операций соответственно.
Последующие \(q\) строк содержат описание выполненных операций. Каждая из последующих \(q\) строк содержит два целых числа \(a\) (\(1 \le a \le 2\)) - тип операции, и \(x\) (\(-100000 \le x \le 100000\)) - число позиций, на которое был произведен циклический сдвиг. Если число \(x\) отрицательно, надо производить циклический сдвиг на \(|x|\) элементов влево, иначе - на \(|x|\) элементов вправо.
Последняя строка содержит \(n\) целых чисел, \(i\)-е из которых - это число, которое будет стоять на \(i\)-й позиции после выполнения операций из условия.
Выходные данные
В единственной строке выведите \(n\) чисел - исходную последовательность.
Система оценки
Подзадача 1 (15 баллов): (\(n \le 100\))
Подзадача 2 (20 баллов): (\(k \le 100\))
Подзадача 3 (65 баллов): без дополнительных ограничений
Примеры
Входные данные
4 2 2 2 2 1 1 3 2 1 0
Выходные данные
0 1 2 3
Входные данные
8 4 4 1 3 1 15 1 -5 2 -1 6 10 14 19 2 16 17 1
Выходные данные
6 10 14 1 2 16 17 19
Входные данные
9 3 5 1 1 2 -8 2 9 1 1 2 -4 3 1 8 7 4 5 2 6 9
Выходные данные
5 3 6 9 7 1 8 2 4
Выбрано
:
|