Темы --> Информатика
    Язык программирования(952 задач)
    Алгоритмы(1657 задач)
    Структуры данных(279 задач)
    Интерактивные задачи(17 задач)
    Другое(54 задач)
---> 2656 задач <---
Источники
    Личные олимпиады(938 задач)
    Командные олимпиады(684 задач)
Страница: << 284 285 286 287 288 289 290 >> Отображать по:
#2918
Числа-подстроки
  
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
64 megabytes

За один шаг к числу X разрешается прибавить или из числа X разрешается вычесть любое положительное число Y, десятичная запись которого является подстрокой десятичной записи числа X. Стоимость такой операции равна сумме цифр числа Y.

Необходимо за минимальную стоимость получить из числа a число b, при этом все промежуточные числа должны быть положительными и не должны превышать n.

Входные данные

Входной файл содержит три целых числа: n, a, b (1 ≤ a, b ≤ n ≤ 5000).

Выходные данные

Если из числа a нельзя получить число b, выведите в выходной файл одно число -1.

Если такая последовательность преобразований существует, в первой строке выходного файла выведите минимальную стоимость требуемого преобразования. Во второй строке выходного файла выведите число k — количество шагов в преобразовании. В последующих k строках выведите сами шаги преобразования по одному в строке. Каждая строка должна иметь вид +число или –число, в зависимости от того, прибавляется или вычитается очередное число.

Примеры
Входные данные
20 12 18
Выходные данные
5
3
-2
+10
-2
Входные данные
100 5 43
Выходные данные
29
8
+5
+1
+1
+1
+13
+26
-5
-4
Входные данные
50 5 43
Выходные данные
-1
#2919
Борьба с пробками
  

Город Нью-Йорк практически парализован гигантским количеством пробок. Мэр Джулио Джулиани предложил новую схему движения по городским улицам. Все улицы по этому плану должны стать односторонними.

Город расположен на прямоугольном острове размером M на N квадратных футов. (M футов с юга на север и N футов с запада на восток. Город разделен на кварталы улицами, идущими с запада на восток и авеню, идущими с юга на север. Длина каждого из кварталов составляет 200 футов (строго говоря, это расстояние между двумя параллельными улицами, окружающими квартал). Улицы нумеруются с юга на север начиная с единицы. Авеню нумеруются с запада на восток также с единицы.

Одностороннее движение организовано так, как показано на рисунке.

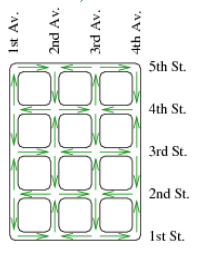
Мэр хочет проехать от одного перекрестка до другого. Определите минимальное расстояние между этими перекрестками. Для простоты можно игнорировать расстояние пройденное на перекрестках, т.е. расстояние пройденное вдоль квартала составляет ровно 200 футов.

Входные данные

Входной файл состоит из 4 строк

Первая строка содержит число M (400 ≤ M ≤ 1000000). Следующая строка содержит число N (400 ≤ N ≤ 1000000). Оба числа делятся на длину квартала. Следующие две строки описывают начальный и конечный перекресток. Каждое описание перекрестка задается так:

m Av., n St.

Например,

1st Av., 5th St.

Выходные данные

Выведите минимальное расстояние между перекрестками.

Примеры
Входные данные
800
600
1st Av., 1st St.
2nd Av., 3rd St.
Выходные данные
1000
#2920
Перекраска полоски
  

Дана полоска Nx1 клетку, каждая клетка которой раскрашена в один из M цветов. За один ход разрешается перекрасить непрерывную область одного цвета в любой другой цвет.

Требуется определить наименьшее число перекрашиваний, за которое можно получить полоску одного (любого) цвета.

Входные данные

В первой строке находятся два числа N и M – ширина полоски и количество цветов соответственно. 1 ≤ N ≤ 100, 1 ≤ M ≤ 100. Во второй строке находятся N чисел, соответствующих цветам каждой из клеток полоски от 1 до N (сами цвета лежат в диапазоне от 1 до M, каждый цвет встречается хотя бы один раз).

Выходные данные

Выведите одно число – минимальное число перекрашиваний, за которое можно получить полоску одного цвета.

Примеры
Входные данные
5 3
3 2 1 1 3
Выходные данные
2
#2926
Киоски с мороженым
  
#2929
Квадрат
  
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
32 megabytes

На плоскости задан квадрат координатами двух своих противоположных вершин. Найти координаты остальных двух вершин квадрата. Результат вывести с точностью до 0,01.

Входные данные

В первой строке вводятся x1 и y1 — координаты одной из вершин квадрата через пробел, во второй строке вводятся x2 и y2 — координаты противоположной вершины квадрата через пробел. Все числа по модулю не превышают 100.

Выходные данные

В первой строке вывести с точностью до 0,01 координаты третьей вершины квадрата x3 и y3 через пробел. Во второй строке вывести с точностью до 0,01 координаты четвертой вершины квадрата x4 и y4 через пробел.

Примеры
Входные данные
7 3
2 4
Выходные данные
5.00000 6.00000
4.00000 1.00000
Страница: << 284 285 286 287 288 289 290 >> Отображать по:
Выбрано
:
Отменить
|
Добавить в контест