Темы --> Информатика --> Алгоритмы
    Задачи на моделирование(78 задач)
    Арифметические алгоритмы(240 задач)
    Алгоритмы поиска(155 задач)
    Алгоритмы сортировки(194 задач)
    Динамическое программирование(355 задач)
    Алгоритмы на графах(319 задач)
    Перебор(154 задач)
    Игры и выигрышные стратегии(33 задач)
    Вычислительная геометрия(216 задач)
    Эвристические методы(30 задач)
    Алгоритмы на строках(45 задач)
    Пересечение множеств(10 задач)
    Жадный алгоритм(71 задач)
    Теория расписаний(5 задач)
    Обработка текста(31 задач)
    Дата и время(14 задач)
---> 1657 задач <---
Источники
    Личные олимпиады(938 задач)
    Командные олимпиады(684 задач)
Страница: << 124 125 126 127 128 129 130 >> Отображать по:
#1154
Скользящая симметрия
  
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
64 megabytes

Движением плоскости называют такое преобразование плоскости, которое сохраняет попарные расстояния между точками, то есть если A1 и B1 – образы некоторых точек A и B при движении, то |A1B1| = |AB|.

Одной из разновидностей движения плоскости является скользящая симметрия. Скользящей симметрией называют композицию симметрии относительно некоторой прямой l и переноса на вектор, параллельный l (этот вектор может быть нулевым). На рисунке показан пример применения скользящей симметрии к отрезку.

 

Известно, что любой отрезок можно перевести в любой другой отрезок такой же длины с помощью скользящей симметрии.

Требуется по координатам двух различных точек A и B и двух точек A1 и B1, находящихся на таком же расстоянии друг от друга, как и точки A и B, найти скользящую симметрию, переводящую точку A в точку A1, а точку B в точку B1.

Входные данные

В первой строке входного файла находятся четыре целых числа – координаты двух различных точек A и В. Во второй строке также находятся четыре целых числа – координаты двух различных точек A1 и В1. Гарантируется, что |A1B1| = |AB|. Все числа во входном файле по модулю не превышают 1000. Числа в строках разделены пробелом.

Выходные данные

Выведите в выходной файл описание искомой скользящей симметрии, которое представляется в следующем виде.

В первой строке должны выводиться координаты двух различных точек, лежащих на прямой l, относительно которой выполняется симметрия, а во второй – координаты вектора, параллельного этой прямой, на который осуществляется перенос. Вещественные числа должны быть представлены не менее чем с 6 знаками после десятичной точки.

Примеры
Входные данные
1 1 3 2
-1 1 -3 2
Выходные данные
0.000000 0.000000 0.000000 1.000000
0.000000 0.000000
Входные данные
1 1 3 1
3 -1 5 -1
Выходные данные
0.000000 0.000000 1.000000 0.000000
2.000000 0.000000
#1155
Трехмерный тетрис
  
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
64 megabytes

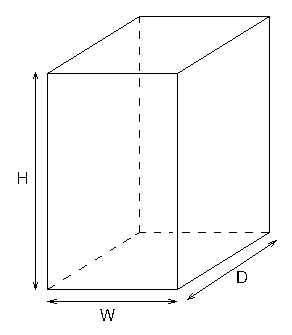
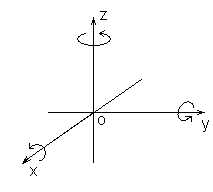Игра в трехмерный тетрис происходит на поле, имеющем вид прямоугольного параллелепипеда размером W×D×H единичных кубиков. Введем координатную систему так, чтобы один из углов параллелепипеда находится в точке (0, 0, 0), противоположный ему – в точке (W, D, H), а ребра параллелепипеда были параллельны осям координаты. Каждый единичный кубик поля можно задать максимальными координатами его углов, тогда кубики будут иметь координаты от (1, 1, 1) до (W, D, H).

В процессе игры на поле последовательно появляются фигуры. Каждая фигура представляет собой множество единичных кубиков и обладает следующим свойством: от любого кубика можно добраться до любого другого, переходя через общую грань.

Игрок может сделать несколько действий с фигурой. Каждое действие является либо перемещением ее на один в направлении одной из осей координат, либо поворотом ее на 90 градусов вокруг одной из координатных осей. Один из кубиков в фигуре является базовым – при поворотах он остается на месте. При повороте фигура сначала исчезает с игрового поля, и затем появляется снова, уже в новом положении. Направления поворотов показаны на рисунке, при повороте вокруг оси OX ось OY переходит в ось OZ, при повороте вокруг оси OY ось OZ переходит в ось OX, при повороте вокруг оси OZ ось OX переходит в ось OY. Базовый кубик при повороте остается на месте.

 

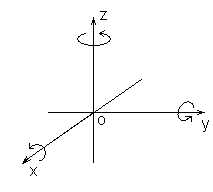Требуется написать программу модуля, ответственного за определение кубиков, которые в результате игры окажутся заняты фигурами. Заранее известна последовательность появления фигур на поле и действия с этими фигурами, которые произвел игрок. Гарантируется, что каждое из действий допустимо, то есть не происходит выхода фигуры за границу поля, и не происходит появления у двух фигур общего кубика.

Входные данные

В первой строке входного файла содержатся размеры игрового поля – три целых числа W, D и H (1 ≤ W, H, D ≤ 100).

Во второй строке входного файла задано целое число n – количество фигур, которые были размещены на игровом поле. (0 ≤ n ≤ 100). Каждая фигура задается следующим образом: на первой строке задано натуральное число m - количество кубиков в фигуре. (1 ≤ m ≤ 100) Далее следуют m строка, в i-й из которых содержится тройка целых чисел xi, yi, zi – координаты i-го кубика в фигуре в ее начальном положении. Базовый кубик описывается первым.

Следующая строка содержит целое число k – количество операций, которые были проведены игроком с данной фигурой (0 ≤ k ≤ 100). Далее следуют k строк. Каждая из них начинается либо со слова «shift», либо со слова «rotate».

В первом случае далее следует одна из букв «x», «y» или «z», обозначающая, вдоль какой из осей был выполнен сдвиг, после чего через пробел идет либо символ «+», если сдвиг был осуществлен в положительном направлении данной оси, либо «–», если сдвиг был осуществлен в отрицательном направлении.

Если же строка начинается со слова «rotate», то далее идет одна из букв «x», «y» или «z», обозначающая, вокруг какой из осей был выполнен поворот.

Выходные данные

Выведите в выходной файл в произвольном порядке координаты всех кубиков, которые будут заняты фигурами. На каждой строке должно содержаться три числа, разделенных пробелом – координаты кубика в формате «x y z».

Примеры
Входные данные
2 2 2
1
2
1 1 1
2 1 1
1
shift z +
Выходные данные
2 1 2
1 1 2
Входные данные
3 3 3
1
4
2 2 2
3 2 2
2 3 2
2 2 3
2
rotate y
rotate z
Выходные данные
2 2 2
2 3 2
2 2 1
1 2 2
#1179
Треугольник
  
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes

На координатной плоскости расположены равнобедренный прямоугольный треугольник ABC с длиной катета d и точка X. Катеты треугольника лежат на осях координат, а вершины расположены в точках: A (0,0), B (d,0), C (0,d).

Напишите программу, которая определяет взаимное расположение точки X и треугольника. Если точка X расположена внутри или на сторонах треугольника, выведите 0. Если же точка находится вне треугольника, выведите номер ближайшей к ней вершины.

Входные данные

Сначала вводится натуральное число d(не превосходящее 1000), а затем координаты точки X – два целых числа из диапазона от ­–1000 до 1000.

Выходные данные

Если точка лежит внутри, на стороне треугольника или совпадает с одной из вершин, то выведите число 0. Если точка лежит вне треугольника, то выведите номер вершины треугольника, к которой она расположена ближе всего (1 – к вершине A, 2 – к B, 3 – к C). Если точка расположена на одинаковом расстоянии от двух вершин, выведите ту вершину, номер которой меньше.

Комментарии к примерам тестов

1. Точка лежит внутри треугольника.

2. Точка лежит вне треугольника и ближе всего к ней вершина A

3. Точка лежит на равном расстоянии от вершин B и C,в этом случае нужно вывести ту вершину, у которой номер меньше, т.е. выведено должно быть число 2

4. Точка лежит на стороне треугольника.

Примеры
Входные данные
5
1 1
Выходные данные
0
Входные данные
3
-1 -1
Выходные данные
1
Входные данные
4
4 4
Выходные данные
2
Входные данные
4
2 2
Выходные данные
0
#1182
Взвешивание
  
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes

Даны двухчашечные весы и набор гирек. На левую чашу весов положили взвешиваемый предмет весом K граммов. Можно ли привести весы в состояние равновесия, и если можно, то определите для каждой чаши весов, какие гирьки на нее для этого нужно положить. Имеющиеся гирьки разрешается класть на любую из чаш весов (каждая гирька имеется только в одном экземпляре, некоторые гирьки можно не использовать).

Входные данные

Вводится сначала K — вес предмета, который положили на левую чашу (1≤K≤50). Далее записано общее количество гирек N (1≤N≤10). Далее записано N различных натуральных чисел, не превышающих 50, — веса гирек.

Выходные данные

В первой строке выведите веса гирек, которые нужно поместить на левую чашу весов, во второй строке — гирьки, которые нужно поместить на правую чашу. Если на какую-то чашу ни одной гирьки помещать не нужно — выведите в этой строке число 0. Если с помощью данных гирек привести весы в равновесие нельзя, выведите одно число –1. Если вариантов несколько, выведите любой из них.

Примеры
Входные данные
5
2
3 5
Выходные данные
0
5
Входные данные
5
3
6 3 4
Выходные данные
4
3 6
Входные данные
5
1
2
Выходные данные
-1
#1184
Найдите последовательность
  
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes

Вася и Петя играют в следующую игру. Они взяли некоторую последовательность символов и дальше получают из нее новые последовательности, отбрасывая несколько первых символов исходной последовательности (разрешается в том числе не отбрасывать ни одного символа, но не разрешается отбрасывать сразу все символы). Каждый называет по одной такой последовательности. Выигрывает тот, чья последовательность будет идти раньше в алфавитном порядке.

Напомним, что если мы сравниваем две последовательности, и у них первые K символов совпадают, а (K+1)-е символы отличаются, то раньше будет идти по алфавиту та, в которой (K+1)-й символ идет раньше по алфавиту. Если же одна последовательность является началом другой, то раньше по алфавиту идет более короткая из них.

Напишите программу, которая по данной последовательности определит, что нужно назвать Васе, чтобы не проиграть Пете.

Входные данные

В первой строке входного файла записано число N — длина исходной последовательности (1≤N≤1000). Во второй строке идет сама последовательность. Последовательность состоит только из заглавных латинских букв.

Выходные данные

В выходной файл выведите выигрышную последовательность.

Примеры

Входные данные

Выходные данные

Комментарии

4

MAMA

A

Рассматриваются строки MAMA, AMA, MA, A. Выигрышная строка A

4

ALLO

ALLO

Выигрышной является исходная строка

5

BBABB

ABB


Страница: << 124 125 126 127 128 129 130 >> Отображать по:
Выбрано
:
Отменить
|
Добавить в контест