Темы --> Информатика --> Алгоритмы
    Задачи на моделирование(78 задач)
    Арифметические алгоритмы(240 задач)
    Алгоритмы поиска(155 задач)
    Алгоритмы сортировки(194 задач)
    Динамическое программирование(355 задач)
    Алгоритмы на графах(319 задач)
    Перебор(154 задач)
    Игры и выигрышные стратегии(33 задач)
    Вычислительная геометрия(216 задач)
    Эвристические методы(30 задач)
    Алгоритмы на строках(45 задач)
    Пересечение множеств(10 задач)
    Жадный алгоритм(71 задач)
    Теория расписаний(5 задач)
    Обработка текста(31 задач)
    Дата и время(14 задач)
---> 1657 задач <---
Источники
    Личные олимпиады(938 задач)
    Командные олимпиады(684 задач)
Страница: << 183 184 185 186 187 188 189 >> Отображать по:
#1990
Кодовый замок - 2
  
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
64 megabytes

Компания «Замки и замки» недавно разработала новый тип кодового замка, для размещения на воротах замков. Панель замка представляет собой прямоугольник шириной \(w\) ячеек и высотой \(h\) ячеек. В некоторых из них расположены кнопки.

Код на этом замке вводится одновременным нажатием \(k\) кнопок. Для того, чтобы код было легче запомнить, используемые в нем кнопки должны образовывать связную область. Область называется связной, если из любой клетки области можно добраться до любой другой, перемещаясь только между клетками этой области с общей стороной. Важным критерием надежности замка является число различных кодов, которые на нем можно набрать.

Для оценки надежности замков требуется написать программу для вычисления указанной величины.

Входные данные

В первой строке входного файла находятся три целых числа \(h\), \(w\) и \(k\) (\(1\le h,w\le 30\); \(1\le k \le 10\)). Каждая из последующих \(h\) строк содержит \(w\) символов. Символ «#» обозначает кнопку, а «.» — ее отсутствие.

Выходные данные

В выходной файл выведите единственное число — количество кодов, удовлетворяющих указанным требованиям.

Примеры

Входные данные Выходные данные
2 2 2
#.
## 		2
5 6 7
.#....
##.##.
..#.#.
.####.
.....# 		3

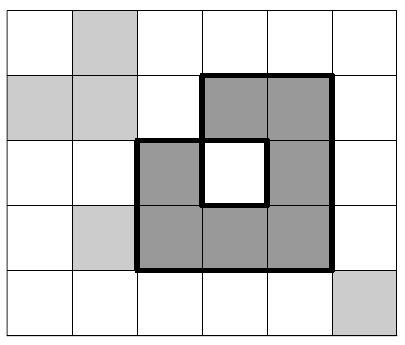
На рисунке изображен один из возможных кодов для второго примера.

#1991
Конденсация графа
  
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes

Вам задан ориентированный граф с \(N\) вершинами и \(M\) ребрами (\(1\le N\le 20 000\), \(1\le M\le 200 000\)). Найдите компоненты сильной связности заданного графа и топологически отсортируйте его конденсацию.

Входные данные

Граф задан во входном файле следующим образом: первая строка содержит числа \(N\) и \(M\). Каждая из следующих \(M\) строк содержит описание ребра — два целых числа из диапазона от \(1\) до \(N\) — номера начала и конца ребра.

Выходные данные

На первой строке выведите число \(K\) — количество компонент сильной связности в заданном графе. На следующей строке выведите \(N\) чисел — для каждой вершины выведите номер компоненты сильной связности, которой принадлежит эта вершина. Компоненты сильной связности должны быть занумерованы таким образом, чтобы для любого ребра номер компоненты сильной связности его начала не превышал номера компоненты сильной связности его конца.

Примеры
Входные данные
10 19
1 4
7 8
5 10
8 9
9 6
2 6
6 2
3 8
9 2
7 2
9 7
4 5
3 6
7 3
6 7
10 8
10 1
2 9
2 7
Выходные данные
2
1 2 2 1 1 2 2 2 2 1
#1993
Отожги мирных ферзей!
  
Темы: [Перебор]
ограничение по времени на тест
3.0 second;
ограничение по памяти на тест
64 megabytes

Расставить \(N\) ферзей на квадратной доске \(N\times N\) так, чтобы никакие два не били друг друга — очень непростая задача. Именно поэтому её поручили вам.

Входные данные

В единственной строке входного файла находится число \(4\le N\le 200\) — размеры доски.

Выходные данные

Выведите \(N\) чисел \(a\): \(a_i\) — это номер горизонтали, на которую вы поставите ферзя, занимающего \(i\)-тую вертикаль. Нумерация горизонталей идёт снизу вверх, от \(1\) до \(N\) (как на обычной шахматной доске).

Пример

Входные данные

Выходные данные

Комментарий

5

5 2 4 1 3

 

#....
..#..
....#
.#...
...#.

#1994
Форд-Беллман - 2
  
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
16 megabytes

В ориентированном взвешенном графе вершины пронумерованы числами от 1 до n. Если i<j, то существует ребро из вершины i в вершину j, вес которого определяется по формуле wt(i,j)=(179i+719j) mod 1000 - 500. Определите вес кратчайшего пути, ведущего из вершины 1 в вершину n.

Входные данные

Программа получает на вход одно число n (2≤n≤13000).

Выходные данные

Программа должна вывести единственное целое число - вес кратчайшего пути из вершины 1 в вершину n в описанном  графе.

Примеры
Входные данные
2
Выходные данные
117
Входные данные
3
Выходные данные
-164
#1995
Авиаперелеты
  
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes

Профессору Форду необходимо попасть на международную конференцию. Он хочет потратить на дорогу наименьшее количество денег, поэтому решил, что будет путешествовать исключительно ночными авиарейсами (чтобы не тратиться на ночевку в отелях), а днем будет осматривать достопримечательности тех городов, через которые он будет проезжать транзитом. Он внимательно изучил расписание авиаперелетов и составил набор подходящих авиарейсов, выяснив, что перелеты на выбранных направлениях совершаются каждую ночь и за одну ночь он не сможет совершить два перелета.

Теперь профессор хочет найти путь наименьшей стоимости, учитывая что до конференции осталось K ночей (то есть профессор может совершить не более K перелетов).

Входные данные

В первой строке находятся числа N (количество городов), M (количество авиарейсов), K (количество оставшихся ночей), S (номер города, в котором живет профессор), F (номер города, в котором проводится конференция).

Ограничения: 2≤N≤100, 1≤M≤105, 1≤K≤100, 1≤S≤N, 1≤F≤N.

Далее идет M строк, задающих расписание авиарейсов. i-я строка содержит три натуральных числа: Si, Fi и Pi, где Si - номер города, из которого вылетает i-й рейс, Fi - номер го-рода, в который прилетает i-й рейс, Pi - стоимость перелета i-м рейсом. 1≤Si≤N, 1≤Fi≤N, 1≤Pi≤106.

Выходные данные

Выведите одно число - минимальную стоимость пути, подходящего для профессора. Если профессор не сможет за K ночей добраться до конференции, выведите число -1.

Примеры
Входные данные
4 5 2 1 4
1 2 1
2 3 1
3 4 1
1 3 3 
1 4 5
Выходные данные
4
Страница: << 183 184 185 186 187 188 189 >> Отображать по:
Выбрано
:
Отменить
|
Добавить в контест