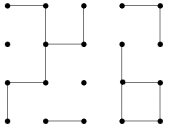
 Печатной схемой называется плоская поверхность содержащей узлы и перемычки, соединяющие пары узлов. Мы будем рассматривать печатные схемы специального вида, где все узлы расположены в узлах прямоугольной сетки, а перемычки (вертикальные или горизонтальные) соединяют пары соседних узлов. Печатная схема называется связной, если любые два узла соединены друг с другом последовательностью перемычек. На вход дается печатная схема, где некоторые соседние узлы уже соединены перемычками. К ней необходимо добавить некоторое количество перемычек таким образом, чтобы схема стала связной. Стоимость вертикальной перемычки – 1, а горизонтальной – 2.
Печатной схемой называется плоская поверхность содержащей узлы и перемычки, соединяющие пары узлов. Мы будем рассматривать печатные схемы специального вида, где все узлы расположены в узлах прямоугольной сетки, а перемычки (вертикальные или горизонтальные) соединяют пары соседних узлов. Печатная схема называется связной, если любые два узла соединены друг с другом последовательностью перемычек. На вход дается печатная схема, где некоторые соседние узлы уже соединены перемычками. К ней необходимо добавить некоторое количество перемычек таким образом, чтобы схема стала связной. Стоимость вертикальной перемычки – 1, а горизонтальной – 2.
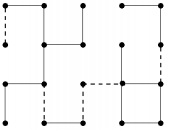 Ваша программа должна по начальной печатной схеме определить количество добавляемых перемычек, минимальную стоимость такого добавления, а также вывести сами добавляемые перемычки.
Ваша программа должна по начальной печатной схеме определить количество добавляемых перемычек, минимальную стоимость такого добавления, а также вывести сами добавляемые перемычки.
Выходные данные
Первая строка должна содержать два числа \(K\) и \(V\) – количество добавленных перемычек и стоимость добавления соответственно. Каждая из следующих \(K\) строк должна содержать описание добавленной перемычки в формате \(i\), \(j\), \(d\), где (\(i\), \(j\)) – координаты начального узла, а \(d\) может принимать значения \(1\) или \(2\). \(d = 1\) обозначает, что соединены узлы (\(i\), \(j\)) и (\(i+1\), \(j\)), \(d = 2\) – узлы (\(i\), \(j\)) и (\(i\), \(j+1\)). Если решений несколько – выведите любое из них.
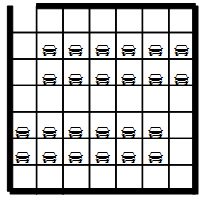
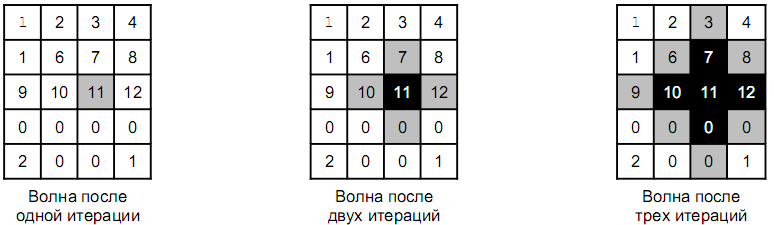
 Печатной схемой называется плоская поверхность содержащей узлы и перемычки, соединяющие пары узлов. Мы будем рассматривать печатные схемы специального вида, где все узлы расположены в узлах прямоугольной сетки, а перемычки (вертикальные или горизонтальные) соединяют пары соседних узлов. Печатная схема называется связной, если любые два узла соединены друг с другом последовательностью перемычек. На вход дается печатная схема, где некоторые соседние узлы уже соединены перемычками. К ней необходимо добавить некоторое количество перемычек таким образом, чтобы схема стала связной. Стоимость вертикальной перемычки – 1, а горизонтальной – 2.
Печатной схемой называется плоская поверхность содержащей узлы и перемычки, соединяющие пары узлов. Мы будем рассматривать печатные схемы специального вида, где все узлы расположены в узлах прямоугольной сетки, а перемычки (вертикальные или горизонтальные) соединяют пары соседних узлов. Печатная схема называется связной, если любые два узла соединены друг с другом последовательностью перемычек. На вход дается печатная схема, где некоторые соседние узлы уже соединены перемычками. К ней необходимо добавить некоторое количество перемычек таким образом, чтобы схема стала связной. Стоимость вертикальной перемычки – 1, а горизонтальной – 2. Ваша программа должна по начальной печатной схеме определить количество добавляемых перемычек, минимальную стоимость такого добавления, а также вывести сами добавляемые перемычки.
Ваша программа должна по начальной печатной схеме определить количество добавляемых перемычек, минимальную стоимость такого добавления, а также вывести сами добавляемые перемычки.