Вашего друга, который до недавних пор работал кондуктором в маршрутке, повысили, и с этих самых недавних пор он является главным экономистом в фирме, владеющей этими маршрутками. К сожалению, он очень быстро обнаружил, что его знаний недостаточно для такой работы, и стал срочно навёрстывать упущенное. К счастью, это оказалось не столь сложно, благо изучать ему требовалось не всю экономику, а только ту её часть, которая имеет отношение к рынку маршруток в крупных городах.
Среди множества моделей, предложенных экономистами для описания различных видов рынков, вашему другу больше всего понравилась знаменитая «модель конного рынка» Е. фон Бём-Баверка. Эта модель состоит в следующем: в базарный день на рыночной площади собрались N продавцов и M покупателей. У каждого продавца есть одна единица товара (принято говорить о конях); каждый покупатель хочет купить одного коня. С точки зрения покупателей, все продавцы и все кони абсолютно одинаковы, т. е. покупателям всё равно, у кого покупать (значение имеет только цена). Аналогично, с точки зрения продавцов все покупатели одинаковы: продавцам всё равно, кому продавать (опять-таки, значение имеет только цена). Но субъективные оценки товара различаются:
- Каждый продавец заранее определил для себя цену, дешевле которой он продавать ни в коем случае не будет: i-й продавец готов продавать коня по цене si и выше.
- Аналогично, каждый покупатель заранее определил для себя цену, дороже которой он покупать ни в коем случае не будет: i-й покупатель готов покупать коня по цене bi и ниже.
Вдобавок к этим условиям, Е. фон Бём-Баверк справедливо полагает, что каждый продавец будет по возможности запрашивать более высокую цену, в то время как каждый покупатель будет стараться купить как можно дешевле. Далее у Бём-Баверка следуют некоторые рассуждения, которые определяют, какие же конкретно сделки произойдут. По мнению вашего друга, эти рассуждения эквивалентны следующим двум условиям:
Все сделки, которые будут совершены, будут совершены по одной цене. Количество продавцов, согласных продавать по этой цене, должно быть равно количеству покупателей и определяет количество сделок.Тем не менее, эти правила всё ещё не определяют однозначно цены, по которым будут совершены сделки. Ваш друг попросил вас написать программу, которая определит нижнюю и верхнюю границу диапазона цен, в котором могут быть совершены сделки. Примечание: Вы не ошиблись: вы действительно находитесь на олимпиаде по информатике, а не по экономике :). Поэтому жюри никоим образом не интересуется, не собирается обсуждать и не гарантирует корректность, правильность, реальность и т. д. предложенной модели. Это — задача по информатике, а не по экономике.
Выходные данные
Если в соответствии с пп. 1 - 4 может произойти хотя бы одна сделка, выведите в выходной файл два числа: сначала нижнюю границу диапазона, потом — верхнюю. Если не произойдёт ни одной сделки, выведите в выходной файл одну строку ‘No solution’ (без кавычек).
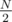 =
=