Система телефонных номеров в России устроена следующим образом. Все телефонные номера имеют одну и ту же длину — M цифр. Номер состоит из двух частей: несколько первых цифр номера составляют код города, остальные цифры определяют номер абонента в пределах этого города.
В процессе развития сети коды городов регулярно меняются, при этом, коды различных городов обязательно различны. В остальном коды могут быть совершенно произвольными, в том числе код одного города может быть началом кода другого (например, код Нижнего Новгорода — 831, а код Сарова — 83130) и т. п. Если коды нескольких городов являются началом M-значного номера абонента, кодом города этого номера считается наидлиннейший из таких кодов. Так, если есть всего четыре города: Нижний Новгород, Балахна, Дзержинск и Саров с кодами, соответственно, 831, 83144, 8313 и 83130, и M = 9, то: телефоны 831123456 и 831412345 — телефоны Нижнего Новгорода, 831312345 — телефон Дзержинска, 831301234 — Сарова, а 831441234 — Балахны.
В этой задаче мы не будем учитывать различные другие ограничения на телефонные номера, существующие в реальности (например, в реальности никакой номер абонента в городе не может начинаться на 03, т. к. 03 — это телефон скорой помощи). Мы будем считать, что любой из 10M возможных M-значных номеров является допустимым телефонным номером.
Нетривиальной задачей становится задача определения, сколько всего телефонных номеров может быть выдано в каждом городе. Например, в приведённом выше примере в Балахне и Сарове могут быть выданы 10 000 телефонных номеров (все четырёхзначные номера), в Дзержинске могут быть выданы 90000 телефонных номеров — все пятизначные телефонные номера, кроме начинающихся на ноль, а в Нижнем Новгороде могут быть выданы 890 000 номеров — все шестизначные номера, кроме тех, которые начинаются на цифру 3, а также на последовательность 44.
Напишите программу, которая решит эту задачу для произвольного набора кодов городов.
Выходные данные
В выходной файл выведите N строк. В каждой строке выведите название города и количество телефонных номеров, которые можно выдать в этом городе. Отделяйте название города и количество номеров как минимум одним пробелом. Вы также можете выводить лишние пробелы в начало и конец каждой строки; они будут игнорироваться.
Города можете выводить в произвольном порядке.
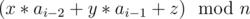 . Первый запрос имеет вид {
. Первый запрос имеет вид {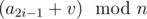 ,
, 