#113904

Обновление дата-центров

Темы: [Компоненты сильной связности] [Обход в глубину]

У компании BigData Inc. есть n дата-центров, пронумерованных от 1 до n , расположенных по всему миру. В этих дата-центрах хранятся данные клиентов компании (как можно догадаться из названия — большие данные!)

Основой предлагаемых компанией BigData Inc. услуг является гарантия возможности работы с пользовательскими данными даже при условии выхода какого-либо из дата-центров компании из доступности. Подобная гарантия достигается путём использования двойной репликации данных. Двойная репликация — это подход, при котором любые данные хранятся в двух идентичных копиях в двух различных дата-центрах.

Про каждого из m клиентов компании известны номера двух различных дата-центров c _{i

, 1} и c _{i

, 2} , в которых хранятся его данные.

Для поддержания работоспособности дата-центра и безопасности данных программное обеспечение каждого дата-центра требует регулярного обновления. Релизный цикл в компании BigData Inc. составляет один день, то есть новая версия программного обеспечения выкладывается на каждый компьютер дата-центра каждый день.

Обновление дата-центра, состоящего из множества компьютеров, является сложной и длительной задачей, поэтому для каждого дата-центра выделен временной интервал длиной в час, в течение которого компьютеры дата-центра обновляются и, как следствие, могут быть недоступны. Будем считать, что в сутках h часов. Таким образом, для каждого дата-центра зафиксировано целое число u _j ( 0 ≤ u _j ≤ h - 1 ), обозначающее номер часа в сутках, в течение которого j -й дата-центр недоступен в связи с плановым обновлением.

Из всего вышесказанного следует, что для любого клиента должны выполняться условия u _{c

_{i

, 1}} ≠ u _{c

_{i

, 2}} , так как иначе во время одновременного обновления обоих дата-центров, компания будет не в состоянии обеспечить клиенту доступ к его данным.

В связи с переводом часов в разных странах и городах мира, время обновления в некоторых дата-центрах может сдвинуться на один час вперёд. Для подготовки к непредвиденным ситуациям руководство компании хочет провести учения, в ходе которых будет выбрано некоторое непустое подмножество дата-центров, и время обновления каждого из них будет сдвинуто на один час позже внутри суток (то есть, если u _j = h - 1 , то новым часом обновления будет 0 , иначе новым часом обновления станет u _j + 1 ). При этом учения не должны нарушать гарантии доступности, то есть, после смены графика обновления должно по-прежнему выполняться условие, что данные любого клиента доступны хотя бы в одном экземпляре в любой час.

Учения — полезное мероприятие, но трудоёмкое и затратное, поэтому руководство компании обратилось к вам за помощью в определении минимального по размеру непустого подходящего подмножества дата-центров, чтобы провести учения только на этом подмножестве.

Входные данные

В первой строке находятся три целых числа n , m и h ( 2 ≤ n ≤ 100 000 , 1 ≤ m ≤ 100 000 , 2 ≤ h ≤ 100 000 ) — число дата-центров компании, число клиентов компании и количество часов в сутках.

Во второй строке вам даны n чисел u ₁ , u ₂ , ..., u _n ( 0 ≤ u _j < h ), j -е из которых задаёт номер часа, в который происходит плановое обновление программного обеспечения на компьютерах дата-центра j .

Далее в m строках находятся пары чисел c _{i

, 1} и c _{i

, 2} ( 1 ≤ c _{i

, 1} , c _{i

, 2} ≤ n , c _{i

, 1} ≠ c _{i

, 2} ), задающие номера дата-центров, на которых находятся данные клиента i .

Гарантируется, что при заданном расписании обновлений в дата-центрах любому клиенту в любой момент доступна хотя бы одна копия его данных.

Выходные данные

В первой строке выведите минимальное количество дата-центров k ( 1 ≤ k ≤ n ), которые должны затронуть учения, чтобы не потерять гарантию доступности. Во второй строке выведите k различных целых чисел — номера кластеров x ₁ , x ₂ , ..., x _k ( 1 ≤ x _i ≤ n ), на которых в рамках учений обновления станут проводиться на час позже. Номера кластеров можно выводить в любом порядке.

Если возможных ответов несколько, разрешается вывести любой из них. Гарантируется, что хотя бы один ответ, удовлетворяющий условиям задачи, существует.

Система оценки

Тесты к этой задаче состоят из трёх групп. Баллы за каждую группу ставятся только при про- хождении всех тестов группы и всех тестов предыдущих групп.

$\text{[math]}$

Примечание

Рассмотрим первый тест из условия. Приведённый ответ является единственным способом провести учения, затронув только один дата-центр. В таком сценарии третий сервер начинает обновляться в первый час дня, и никакие два сервера, хранящие данные одного и того же пользователя, не обновляются в один и тот же час.

С другой стороны, например, сдвинуть только время обновления первого сервера на один час вперёд нельзя — в таком случае данные пользователей 1 и 3 будут недоступны в течение нулевого часа.

Примеры

Входные данные

Выходные данные

1
3

Входные данные

Выходные данные

4
1 2 3 4

#113935

Лабиринт

Темы: [0-1 BFS] [Алгоритм Дейкстры]

В одном из уровней компьютерной игры вы попали в лабиринт, состоящий из n строк, каждая из которых содержит m клеток. Каждая клетка либо свободна, либо занята препятствием. Стартовая клетка находится в строке r и столбце c . За один шаг вы можете переместиться на одну клетку вверх, влево, вниз или вправо, если она не занята препятствием. Вы не можете перемещаться за границы лабиринта.

К сожалению, ваша клавиатура крайне близка к поломке, поэтому вы можете переместиться влево не более x раз и вправо не более y раз. При этом ограничений на перемещения вверх и вниз нет, поскольку клавиши, используемые для движения вверх и вниз, всё ещё в идеальном состоянии.

Теперь вы для каждой клетки поля решили установить, можно ли выбрать такую последовательность нажатий, которая приведёт вас из стартовой в эту клетку. Посчитайте, сколько клеток поля обладают таким свойством.

Входные данные

Первая строка содержит два целых числа n , m ( 1 ≤ n , m ≤ 2000 ) — количество строк и столбцов в лабиринте, соответственно.

Вторая строка содержит два целых числа r , c ( 1 ≤ r ≤ n , 1 ≤ c ≤ m ) — номер строки и столбца, на пересечении которых расположена стартовая клетка.

Третья строка содержит два целых числа x , y ( 0 ≤ x , y ≤ 10 ⁹ ) — максимальное количество перемещений влево и вправо, соответственно.

Следующие n строк содержат описание лабиринта. Каждая из этих строк имеет длину m и состоит только из символов ' . ' и ' * '. В i -й строке j -й символ соответствует клетке лабиринта с номерами строки и столбца i и j , соответственно. Символ ' . ' соответствует свободной клетке лабиринта, а символ ' * ' — клетке с препятствием.

Гарантируется, что стартовая клетка не занята препятствием.

Выходные данные

Выведите одно число — количество клеток лабиринта, достижимых из стартовой, включая её саму.

Примечание

Клетки, достижимые в соответствующем примере, отмечены ' + '.

Первый пример


+++..
+***.
+++**
*+++.

Второй пример


.++.
.+*.
.++.
.++.

Примеры

Входные данные

4 5
3 2
1 2
.....
.***.
...**
*....

Выходные данные

Входные данные

4 4
2 2
0 1
....
..*.
....
....

Выходные данные

#113940

Петербург?

Темы: [Интерактивные задачи] [Мосты] [Алгоритмы на графах]

– Это что за остановка – Бологое иль Поповка? – А с платформы говорят: – Это город Ленинград.

«Вот какой рассеянный», Самуил Маршак

Пытаясь спастись от мира спортивного программирования, Алина сбежала на вокзал и уехала прочь на ночной электричке. Минуты медленно уплывали в даль, и уставшую девочку клонило в сон. Ей снился город-сказка, где не надо программировать, а можно гулять, мечтать и наслаждаться жизнью. Внезапно дождь из интерактивных задач разрушил эту идиллию.

Проснувшись и открыв окно, Алина задалась вопросом весьма философского свойства: «Где я?». С перрона потерявшейся девочке сообщили, что этот город, не похожий ни на что вокруг, представляет собой неориентированный граф на $n$ вершинах и $m$ ребрах. Сeй невероятный факт, однако, нисколько не удивил Алину. Она давно мечтала побывать в одном таком городе — Петербурге. Его уникальной отличительной особенностью является то, что хотя бы половина его ребер — мосты (определение дано в конце условия). Так как никакие другие города Алине не интересны, она решила ограничиться расспросом находящихся на платформе эрудированных путешественников. Любой из их них может по данной вершине $v$ сообщить любое ещё не названное ребро, исходящее из нее, или же заявить об отсутствии таковых.

Алина неуверена в своих силах, поэтому попросила вас помочь ей определить, попала ли она в Петербург. Так как её поезд скоро продолжит свой путь, задать больше $3n$ вопросов не получится.

Обратите внимание, что в графе могут присутствовать петли и кратные ребра.

Протокол взаимодействия

В первой строке стандартного потока ввода даны два целых числа $n$ и $m$ ($1 \le n, m \le 100\,000$) — число вершин и ребер в графе соответственно.

Для того, чтобы узнать очередное ребро, исходящее из $u$-й вершины ($1 \le u \le n$), нужно вывести « ? $u$ ». После этого ваша программа на вход получит целое число $v$ ($-2 \le v \le -1$ или $1 \le v \le n$) — $v = a + b - u$, если существует ребро $ab$, которое инцидентно вершине $u$ и ещё не было названо , $-1$, если такого ребра не существует и $-2$, если вы превысили допустимое число запросов. В последнем случае ваша программа должна немедленно завершиться, в ином случае жюри не гарантирует корректность полученного вами вердикта.

Вам разрешается задать не более $3n$ вопросов.

Чтобы сообщить, что ответ найден, требуется вывести « ! Yes » или « ! No », в зависимости от того, является ли загаданный граф Петербургом. В случае положительного ответа выведите $\lceil\frac{m}{2}\rceil$ строк, по два целых числа $u_i$ и $v_i$ в каждой ($1 \le u_i, v_i \le n$), обозначающих, что ребро $(u_i, v_i)$ является мостом. Любое ребро в приведенном списке должно встречаться не более одного раза (кратные ребра считаются различными).

Запрос на вывод ответа не входит в ограничение на $3n$ запросов.

Не забывайте сбрасывать буфер после каждого запроса. Например, на языке C++ надо использовать функцию fflush(stdout) или вызов cout.flush() , на Java вызов System.out.flush() , на Pascal flush(output) и stdout.flush() для языка Python.

Система оценки

Подзадача 0. Тесты из условия

Подзадача 1. (27 баллов) $N, M \leq 10$. Пройдена подзадача 0.

Подзадача 2. (30 баллов) $N \leq 10000, M \leq 20000$. Пройдена подзадача 1.

Подзадача 3. (1 балл за каждый пройденный тест) Нет дополнительных ограничений. Пройдена подзадача 2.

Примечание

В условии в примере взаимодействия вводимые и выводимые данные расположены для удобства восприятия в хронологическом порядке, при реальном взаимодействии никакие «лишние» переводы строк возникать не должны.

Ввод-вывод в примерах демонстрирует пример взаимодействия вашей программы с проверяющей системой.

В первом примере был загадан граф на трех вершинах с ребрами $(1, 2)$, $(2, 3)$ и $(3, 1)$.

Во втором примере была загадан граф на четырех вершинах с ребрами $(1, 2)$, $(2, 3)$, $(3, 4)$ и $(2, 3)$.

Ребро, соединяющее вершины $u$ и $v$, называется мостом, если после его удаления между вершинами $u$ и $v$ не существует пути.

Примеры

Входные данные

Выходные данные

? 3

? 1

? 2

? 1

? 1

? 3

! No

Входные данные

Выходные данные

? 1

? 2

? 3

? 1

? 3

? 3

? 2

? 4

! Yes
1 2
3 4

#113948

LinkedList's Bizarre Adventure

Темы: [Игры и выигрышные стратегии] [Простые игры] [Деревья]

В двусвязном списке, он же LinkedList, каждый элемент может быть связан максимум с двумя другими элементами — с предыдущим элементом (если он есть) и со следующим элементом (если он есть).

Билли и Рикардо проходят стажировку в компании FlexDex в группе поддержки внутреннего анонимного форума с возможностью деанонимизации. Для представления последовательных сообщений в теме необходимо использовать список, где элементами будут являться эти сообщения, и два товарища решили написать свою быструю реализацию двусвязного списка FlexList.

Но у них что-то пошло не так — в их списке новое сообщение может связываться не только с первым или последним сообщением, как должно быть, а с любым из уже существующих сообщений.

Если представить каждое сообщение как вершину графа, а связи между сообщениями как ребра графа, то гарантируется, что этот граф будет неориентированным, связным и ацикличным.

Говорится, что граф является корректным графом, если в этом графе у каждой вершины не более двух вершин, связанных с ней ребром. Изначально же FlexList связи между сообщениями могут выглядеть в виде любого связного ацикличного графа, не обязательно корректного.

Билли и Рикардо не растерялись и решили, что будут вручную исправлять все неясности в ходе работы программ, которые используют их изобретение. Тимлид дал им тестовый пример для проверки кода. Они получили на этом примере граф связей и вручную делают из него корректный граф, ведь связи между сообщениями в корректном двусвязном списке могут представлять собой только корректный граф.

Это выглядит так — сначала Билли проверяет, что граф корректный. Если это не так, то он выбирает и удаляет некоторый лист (вершина, у которой есть ровно одна связь с другими вершинами), и отдает граф Рикардо, затем Рикардо делает то же самое и отдает граф Билли, и так продолжается до тех пор, пока кто-то не получит от товарища корректный граф. Как только один из двух друзей получает такой граф, то тут же показывает его тимлиду, с надеждой на похвалу и повышение в должности.

Каждый хочет получить первым такой граф. Кто первым попадет к тимлиду, если оба товарища удаляют листья оптимально для себя?

Входные данные

В первой строке содержится одно целое число $n$ ($1 \leq n \leq 300\,000$) — число сообщений в примере тимлида. Следующие $n - 1$ строк задают связи между сообщениями. Каждая из них содержит два целых числа $a_i$ и $b_i$ ($1 \leq a_i, b_i \leq n$, $a_i \neq b_i$), которые показывают, что сообщения с номерами $a_i$ и $b_i$ связаны.

Выходные данные

Выведите "Billy" (без кавычек), если первым попадет к тимлиду Билли, иначе выведите "Ricardo" (без кавычек).

Примечание

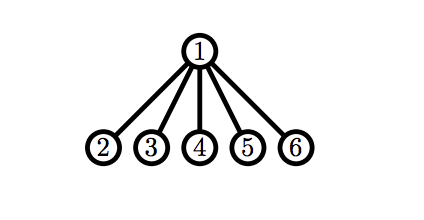
В первом примере Билли первым ходом может удалить одну из вершин с номерами $2$, $4$ или $5$, так как они являются листьями. Он не будет удалять вершину с номером $4$ или $5$, так как в таком случае он передаст Рикардо корректный граф и проиграет. Значит, он удалит вершину $2$. В свою очередь, Рикардо может удалить вершины $1$, $4$ или $5$, и, в любом случае, Билли получит от него корректный граф.

$\text{[math]}$

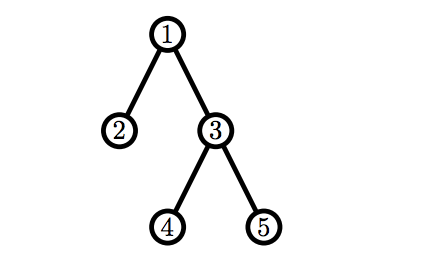
Во втором примере у Билли сразу есть корректный граф.

$\text{[math]}$

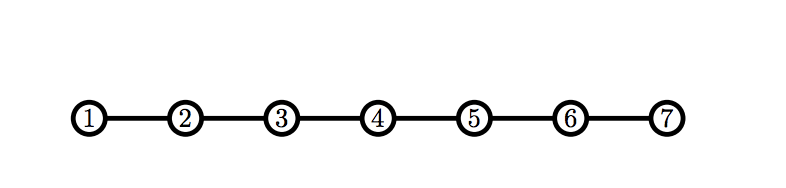
В третьем примере можно показать, что вне зависимости от ходов Билли, Рикардо получит корректный граф первым.

$\text{[math]}$

Примеры

Входные данные

Выходные данные

Billy

Входные данные

Выходные данные

Billy

Входные данные

Выходные данные

Ricardo

#114091

Топологическая сортировка

Темы: [Обход в глубину]

Задан ориентированный ациклический граф с $n$ вершинами и $m$ ребрами. Также задана перестановка вершин графа. Необходимо проверить, является ли данная перестановка топологической сортировкой.

Входные данные

В первой строке даны два числа $n$ и $m$ — количество вершин и ребер в графе соответственно ($1 \leq n, m \leq 10^5$). В следующих $m$ строках заданы пары чисел $u_i, v_i$, означающие, что в графе есть ребро из вершины $u_i$ в вершину $v_i$. В последней строке задана перестановка из $n$ элементов.

Выходные данные

Выведите "YES" (без кавычек), если данная перестановка является топологической сортировкой и "NO" в противном случае.

Примеры

Входные данные

Выходные данные

NO

Входные данные

Выходные данные

YES