Темы --> Информатика --> Структуры данных
    Деревья(174 задач)
    Линейные структуры(59 задач)
    Корневая эвристика (sqrt декомпозиция)(14 задач)
    Разреженные таблицы (sparse table)(2 задач)
    Система непересекающихся множеств(16 задач)
    Хеш(35 задач)
    Персистентные структуры данных(2 задач)
---> 279 задач <---
Источники
    Личные олимпиады(938 задач)
    Командные олимпиады(684 задач)
Страница: << 45 46 47 48 49 50 51 >> Отображать по:
#113545
Иллюзия сортировки
  
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
512 megabytes

Известный программист пробует себя в роли иллюзиониста. Его коронный фокус состоит в следующем.

Для заданного массива из n целых неотрицательных чисел a1, a2, ..., an он быстро подбирает магическое число b. Целое неотрицательное число b называется магическим для массива, если применение операции побитового исключающего ИЛИ с этим числом к каждому элементу массива превращает его в отсортированный массив. Иначе говоря,

\(\) (a_1\oplus b) \le (a_2\oplus b) \le ... \le (a_n\oplus b) \(\)

где \(\oplus\) — операция побитового исключающего ИЛИ.

Чтобы фокус был более эффектным, после предъявления магического числа для заданного массива иллюзионист q раз выполняет следующее действие. Он предлагает зрителям изменить один из элементов массива и после этого снова пытается предъявить магическое число. При этом программист настолько отточил свое мастерство иллюзиониста, что каждый раз предъявляет зрителям минимальное возможное магическое число. Иногда фокус не удаётся, так как для полученного массива невозможно подобрать магическое число.

Требуется написать программу, которая по заданному исходно массиву, а также после каждого изменения элемента, вычисляет минимальное магическое число для полученного массива, либо определяет, что такого числа нет.

Примечание

Исключающее ИЛИ — это логическая операция, обозначаемая знаком \(\oplus\), которая задаётся следующей таблицей истинности:

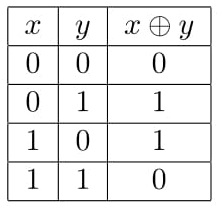
Определим побитовое исключающее ИЛИ для двух неотрицательных целых чисел x и y. Запишем каждое из целых чисел x и y в двоичной системе счисления, дополнив при необходимости более короткое из чисел ведущими нулями до равной длины. Побитовое исключающее ИЛИ двух целых чисел \(x\) и \(y\), обозначаемое также как \(\oplus\), это целое неотрицательное число, каждый разряд которого в двоичной системе счисления является исключающим ИЛИ соответствующих разрядов чисел \(x\) и \(y\). Например, \(5\oplus22=101_2\oplus10110_2=10011_2=19\).

Среди предложенных на олимпиаде языков программирования в языке Паскаль для обозначения исключающего ИЛИ используется оператор «xor», в остальных языках программирования используется оператор «^».

Входные данные

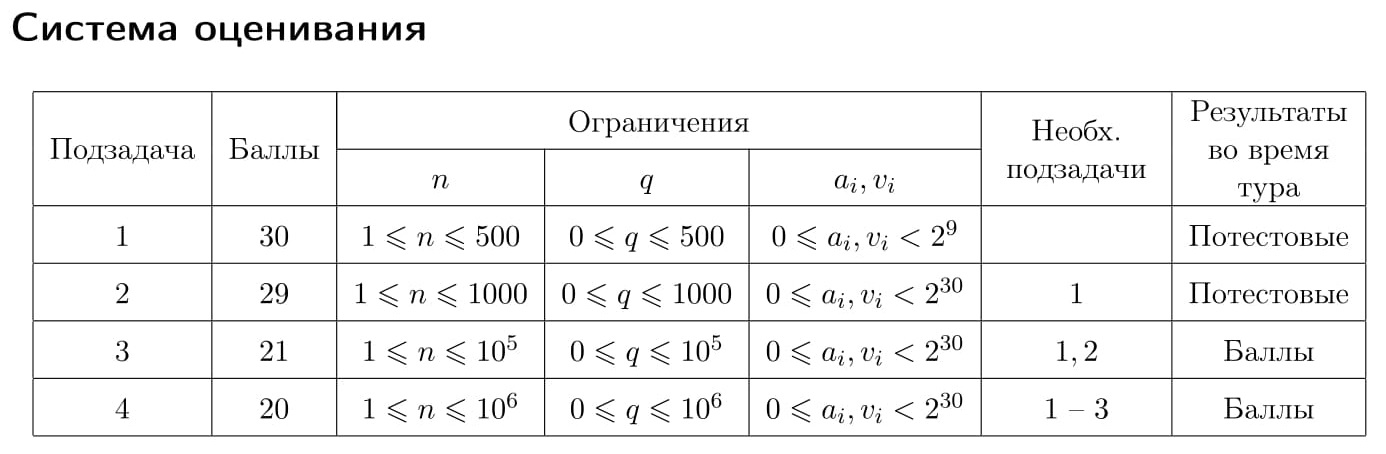
Первая строка входных данных содержит целое число n — количество чисел в массиве (1 ≤ n ≤ 106).

Вторая строка содержит n целых чисел a1, a2, ..., an — элементы массива (0 ≤ ai < 230).

Третья строка содержит целое число q — число изменений элемента массива (0 ≤ q ≤ 106).

Следующие q строк содержат по два целых числа pi и vi, где pi — номер элемента массива, который следует заменить (1 ≤ pi ≤ n), а vi — новое значение этого элемента (0 ≤ vi < 230).

Выходные данные

Выходные данные должны содержать (q + 1) целых чисел b0, b1, ..., bq, по одному в строке.

Значение b0 — либо минимальное возможное магическое число для исходного массива, либо  - 1, если такого числа не существует.

Для i от 1 до q значение bi — либо минимальное возможное магическое число для массива после первых i изменений, либо  - 1, если такого числа не существует.

Примеры
Входные данные
3
0 1 4
3
2 7
3 3
1 4
Выходные данные
0
2
-1
4
#113548
Накопитель
  
Темы: [Стек]
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
512 megabytes

Исследуется новое цифровое устройство для хранения информации. Информация на устройстве хранится в виде последовательности ячеек, каждая из которых находится в одном из двух состояний, обозначаемых символами «+» и «-», и, таким образом, хранит один бит информации.

Назовём фрагментом группу соседних ячеек с одинаковым состоянием, слева от которой либо нет ячеек, либо находится ячейка в противоположном состоянии, и справа — либо нет ячеек, либо находится ячейка в противоположном состоянии.

Операция записи позволяет выбрать любую пару соседних фрагментов разной длины и изменить состояние всех ячеек более короткого фрагмента на противоположное, объединяя таким образом два или три соседних фрагмента в один.

Требуется написать программу, которая по заданной исходной и итоговой последовательностям состояний ячеек определяет, можно ли из исходной последовательности получить итоговую с помощью последовательных операций записи.

Входные данные

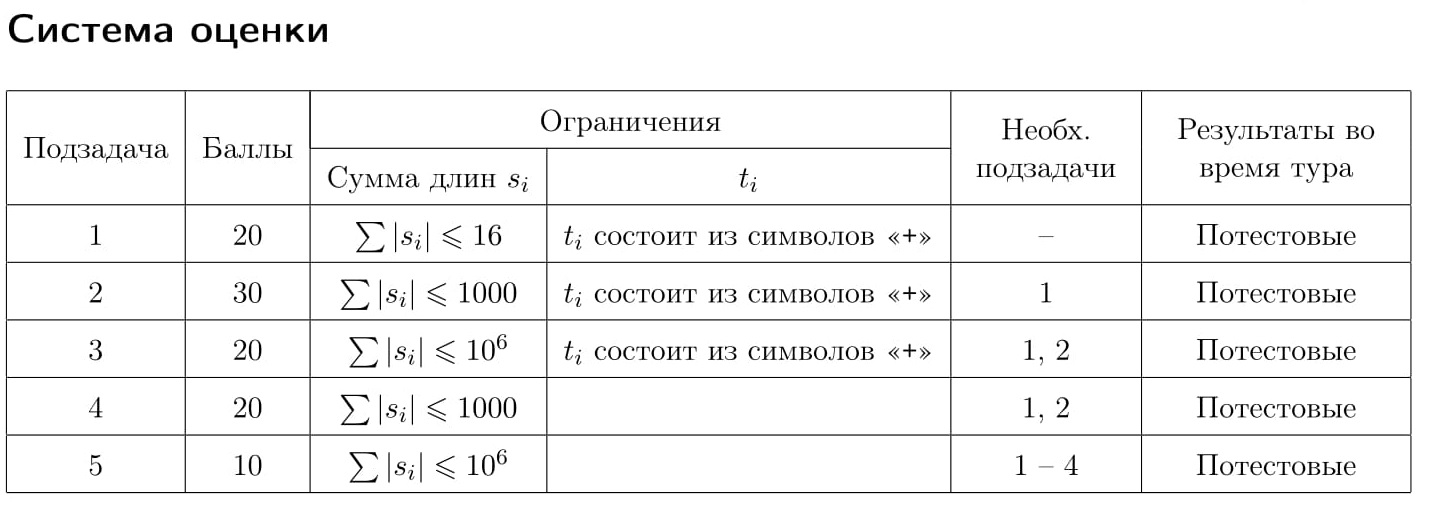
Первая строка входных данных содержит целое положительное число q — количество тестов.

Каждая из следующих q строк содержит si, ti — непустые последовательности символов «+» и «-» одинаковой длины, разделённые одним пробелом. Эта строка означает, что в тесте номер i из исходной последовательности состояний ячеек si требуется получить итоговую последовательность ti.

Выходные данные

Выходные данные должны содержать q строк, где i-я строка равна «Yes», если из исходной последовательности состояний ячеек si можно получить итоговую последовательность ti, или «No» в противном случае.

Примеры
Входные данные
3
++- +++
++-- ++++
++-+--+- ++++++++
Выходные данные
Yes
No
Yes
Входные данные
3
++-+-- ++----
++-+-- +++---
-++- -++-
Выходные данные
Yes
No
Yes
#113550
Антивещество
  
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
128 megabytes

Компания тестирует технологию получения антивещества, используемого в качестве топлива в межпланетном звездолёте. Антивещество получается в результате специальных экспериментов в реакторе.

Известно n типов экспериментов, приводящих к получению антивещества. В результате проведения эксперимента i-го типа в выходной контейнер реактора добавляется от li до ri граммов антивещества. Из соображений безопасности запрещается накапливать в контейнере более a граммов антивещества.

Затраты на проведение эксперимента i-го типа составляют ci, а стоимость одного грамма полученного антивещества составляет 109.

Если после проведения экспериментов в контейнере образовалось t граммов антивещества, а суммарные затраты на проведение экспериментов в реакторе составили s, то прибыль определяется по формуле (t·109 - s). Компании необходимо разработать стратегию проведения экспериментов, позволяющую максимизировать прибыль, которую можно гарантированно получить.

В зависимости от результатов предыдущих экспериментов стратегия определяет, эксперимент какого типа следует провести, или решает прекратить дальнейшее выполнение экспериментов. Стратегия позволяет гарантированно получить прибыль x, если при любых результатах проведения экспериментов: во-первых, в контейнере реактора оказывается не более a граммов антивещества, во-вторых, прибыль составит не менее x.

Например, пусть возможен только один тип эксперимента, порождающий от 4 до 6 граммов антивещества, затраты на его проведение равны 10, а вместимость контейнера составляет 17 граммов. Тогда после двукратного проведения эксперимента в контейнере может оказаться от 8 до 12 граммов антивещества. Если получилось 12 граммов, то больше проводить эксперимент нельзя, так как в случае получения 6 граммов антивещества контейнер может переполниться. В остальных случаях можно провести эксперимент в третий раз и получить от 12 до 17 граммов антивещества. В худшем случае придётся провести эксперимент трижды, затратив в сумме 30, прибыль составит (12·109 - 30) = 11 999 999 970.

Требуется написать программу, которая определяет максимальную прибыль x, которую гарантированно можно получить.

Входные данные

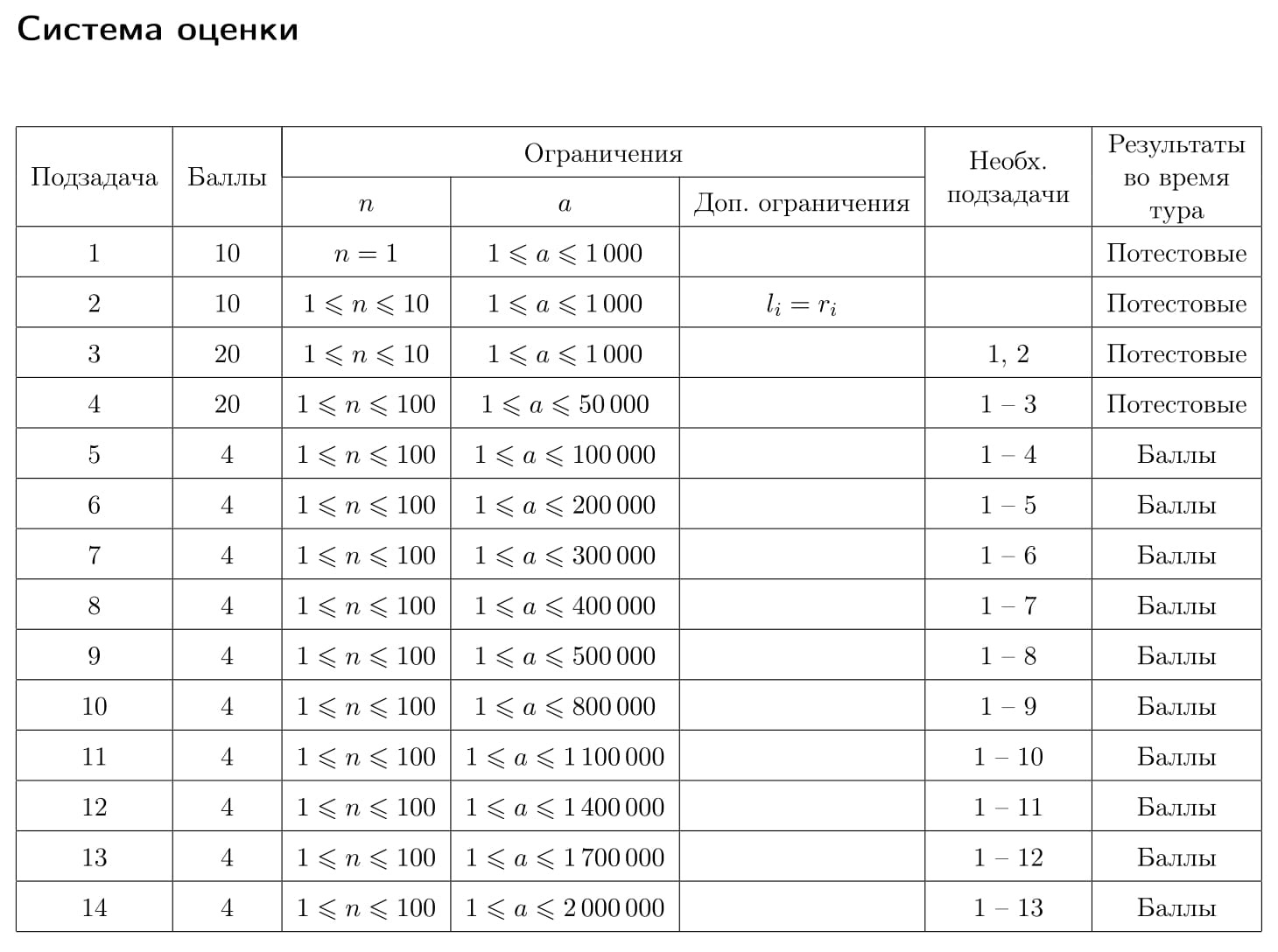
Первая строка входных данных содержит два целых числа: n — количество типов экспериментов и a — максимально допустимое количество антивещества в контейнере (1 ≤ n ≤ 100, 1 ≤ a ≤ 2 000 000).

Следующие n строк содержат по три целых числа li, ri и ci — минимальное и максимальное количество антивещества, получаемое в результате эксперимента типа i, и затраты на эксперимент этого типа, соответственно (1 ≤ li ≤ ri ≤ a, 1 ≤ ci ≤ 100).

Выходные данные

Выходные данные должны содержать одно целое число — максимальную прибыль x, которую гарантированно можно получить.

Примеры
Входные данные
1 17
4 6 10
Выходные данные
11999999970
Входные данные
2 11
2 2 100
3 5 5
Выходные данные
9999999890
#113551
Траектория обучения
  
Темы: [Рекурсия] [Стек]
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
512 megabytes

Победитель студенческой олимпиады получил предложения о стажировке от двух университетов. При подготовке планов обучения он узнал рейтинг качества преподавания каждой дисциплины в этих университетах.

Программа обучения первого университета состоит из последовательности перечисленных в хронологическом порядке n различных дисциплин a1, a2, ..., an, имеющих рейтинги x1, x2, ..., xn соответственно. Программа обучения второго университета состоит из последовательности перечисленных в хронологическом порядке m различных дисциплин b1, b2, ..., bm, имеющих рейтинги y1, y2, ..., ym соответственно.

Студент имеет возможность составить план обучения в первом университете таким образом, чтобы изучить дисциплины на позициях учебной программы с la по ra включительно (1 ≤ la ≤ ra ≤ n), либо отказаться от стажировки в первом университете. Аналогично он может составить план обучения во втором университете таким образом, чтобы изучить дисциплины на позициях учебной программы с lb по rb включительно (1 ≤ lb ≤ rb ≤ m), либо отказаться от стажировки во втором университете.

Изучать одну и ту же дисциплину дважды в разных университетах не имеет смысла, поэтому все дисциплины в двух выбранных планах обучения должны быть различны.

Требуется написать программу, которая определит планы обучения студента таким образом, чтобы получить наибольшую возможную сумму рейтингов изучаемых дисциплин.

Входные данные

Первая строка входных данных содержит целые числа n и m — количество дисциплин в программах обучения первого и второго университетов (1 ≤ n, m ≤ 500 000).

Вторая строка входных данных содержит n целых чисел ai — дисциплины, входящие в программу обучения первого университета, перечисленные в хронологическом порядке (1 ≤ ai ≤ n + m).

Третья строка входных данных содержит n целых чисел xi — рейтинги дисциплин, входящих в программу обучения первого университета, перечисленные том же порядке, что и дисциплины ai (1 ≤ xi ≤ 109).

Четвёртая строка входных данных содержит m целых чисел bi — дисциплины, входящие в программу обучения второго университета, перечисленные в хронологическом порядке (1 ≤ bi ≤ n + m).

Пятая строка входных данных содержит m целых чисел yi — рейтинги дисциплин, входящих в программу обучения второго университета, перечисленные том же порядке, что и дисциплины bi (1 ≤ yi ≤ 109).

Выходные данные

Первая строка выходных данных должна содержать целое число r — наибольшую возможную сумму рейтингов дисциплин.

Вторая строка выходных данных должна содержать целые числа la, ra — позиции в учебной программе первой и последней дисциплин, входящих в план обучения в первом университете, либо «0 0», если студент отказался от стажировки в первом университете.

Третья строка выходных данных должна содержать целые числа lb, rb — позиции в учебной программе первой и последней дисциплин, входящих в план обучения во втором университете, либо «0 0», если студент отказался от стажировки во втором университете.

Если возможных правильных ответов несколько, разрешается вывести любой из них.

Примечание

В первом тесте из условия приведённые планы обучения в университетах приводят к суммарному рейтингу дисциплин (7 + 4 + 10 + 1 + 5) + (5 + 3 + 4) = 27 + 12 = 39. Если бы студент выбрал только вторую и третью дисциплины в первом университете и весь курс обучения во втором университете, суммарный рейтинг дисциплин был бы (7 + 4) + (3 + 5 + 3 + 4 + 12) = 11 + 27 = 38.

Во втором тесте из условия первая и третья дисциплины во втором университете имеют настолько высокий рейтинг по сравнению с соответствующими дисциплинами первого университета, что наиболее выгодный вариант — пройти целиком стажировку во втором университете и отказаться от стажировки в первом университете.

Примеры
Входные данные
7 5
3 1 4 8 6 9 2
2 7 4 10 1 5 3
9 2 11 3 8
3 5 3 4 12
Выходные данные
39
2 6
2 4
Входные данные
2 3
1 2
1 4
2 3 1
17 2 15
Выходные данные
34
0 0
1 3
Входные данные
3 3
4 2 1
10 1 2
5 4 2
1 2 9
Выходные данные
19
1 1
3 3
#113555
Генерал Хенрик
  
Источники: [ Личные олимпиады, COCI, COCI 2015-2016, Раунд 2, Генерал Хенрик ]
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes

Известно, что в солнечной системе есть 8 планет и один планетоид. Мало кто знает, что ещё есть секретная планета, населенная медведями. Именно туда ассоциация Savez отправляет бравого генерала Хенрика для изучения медведей. Выяснилось, что медведи умеют телепортироваться. Расчётливый генерал Хедрик решил завербовать их в свою армию.

У одного медведя есть N строк (обозначим i -ю из них x i ). Исследования показывают, что количество раз, которое может телепортироваться медведь равно длине наибольшей подпоследовательности этих строк, удовлетворяющей такому правилу: строки x i и x j ( i < j ) могут принадлежать одной такой последовательности, если x i является и префиксом, и суффиксом x j .

Помогите уставшему от долгого полёта генералу Хендрику определить, сколько телепортаций сможет сделать данный медведь.

Входные данные

В первой строке содержится одно целое число N – количество строк, которые есть у медведя. В последующих N строках содержатся сами эти строки. Входной файл содержит не более двух миллионов символов.

Выходные данные

Выведите одно число – ответ на вопрос любопытного генерала Хендрика.

Примечание

В первом примере наибольшая последовательность A -> AA -> AAA В третьем примере наибольшая последовательность A -> A -> A или B -> B -> B

Примеры
Входные данные
5
A
B
AA
BBB
AAA
Выходные данные
3
Входные данные
5
A
ABA
BBB
ABABA
AAAAAB
Выходные данные
3
Входные данные
6
A
B
A
B
A
B
Выходные данные
3
Страница: << 45 46 47 48 49 50 51 >> Отображать по:
Выбрано
:
Отменить
|
Добавить в контест