Стек(35 задач)
Дек(6 задач)
Список(7 задач)
Префиксные суммы(минимумы, ...)(2 задач)
Известно, что если сохранить в каждом слове текста первую и последнюю букву, а остальные переставить произвольным образом, получившийся текст по-прежнему можно достаточно свободно прочитать. В лаборатории информатики исследуют аналогичный феномен для числовых последовательностей.
Будем называть последовательность, состоящую из целых положительных чисел, корректной , если первое число в этой последовательности является минимальным, а последнее — максимальным. Например, последовательности [1, 3, 2, 4] и [1, 2, 1, 2] являются корректными, а последовательность [1, 3, 2] — нет.
Задана последовательность [ a 1 , a 2 , ..., a n ] . Будем называть отрезок элементов заданной последовательности [ a l , a l + 1 , ..., a r ] корректным, если он представляет собой корректную последовательность: a l является минимальным числом на этом отрезке, а a r — максимальным.
В рамках исследования необходимо разбить заданную последовательность на минимальное количество непересекающихся корректных отрезков. Например, последовательность [2, 3, 1, 1, 5, 1] можно разбить на три корректных отрезка: [2, 3] и [1, 1, 5] и [1] .
Требуется написать программу, которая по заданной последовательности определяет, на какое минимальное количество корректных отрезков её можно разбить.
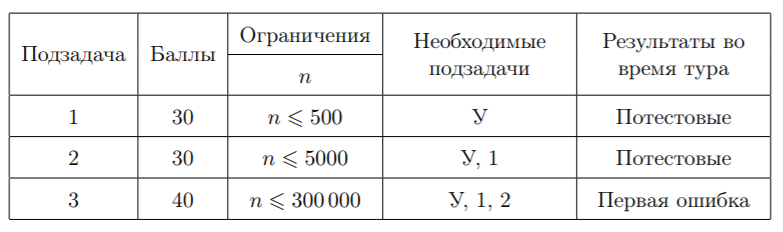
Первая строка входных данных содержит целое число n ( 1 ≤ n ≤ 300 000 ) — количество элементов в заданной последовательности.
Вторая строка содержит n целых чисел a 1 , a 2 , ..., a n — заданную последовательность ( 1 ≤ a i ≤ 10 9 ).
Выведите одно число — минимальное количество корректных отрезков, на которое можно разбить заданную последовательность.
5 5 4 3 2 1
5
4 1 3 2 4
1
6 2 3 1 1 5 1
3
В Берляндии по воскресеньям проходит известое шоу — игра «Слабое звено».
В игре принимают участие \(n\) игроков, которые выстраиваются в круг. Каждому игроку сопоставлен рейтинг — некоторое целое число \(a_i\).
Игра проходит в несколько раундов, каждый из которых выглядит следующим образом:
Можно показать, что если до очередного раунда в игре оставалось хотя бы три участника, то после одного раунда гарантированно останется не менее двух участников.
Вам нужно выяснить для каждого участника, останется ли он до конца, или номер раунда, в котором он покинет игру.
В первой строке дано одно целое число \(n\) (\(2 \le n \le 200\,000\)) — количество участников в игре.
Вторая строка содержит \(n\) целых чисел \(a_i\) (\(1 \le a_i \le 200\,000\)) — рейтинги всех участников игры в том порядке, в котором они стоят, при этом участник с номером \(n\) является соседом участника с номером \(1\).
Выведите \(n\) целых чисел — номер раунда, в котором участник игры с номером \(i\) покинет игру, или \(0\), если этот игрок останется до конца игры.
Раунды нумеруются последовательными целыми числами начиная с \(1\).
В первом примере игра проходит следующим образом (при помощи _ обозначаются выбывшие участники):
\([4; 5; 5; 2; 3] \to [4; 5; 5; \_; 3] \to [4; 5; 5; \_; \_] \to [\_; 5; 5; \_; \_]\)
После этого игра заканчивается, так как осталось ровно два человека.
Во втором примере игра проходит следующим образом:
\([5; 1; 3; 1; 5] \to [5; \_; 3; \_; 5] \to [5; \_; \_; \_; 5]\)
В третьем и чётвертом примере нет ни одного игрока, который был бы одновременно слабее обоих своих соседей, поэтому игра заканчивается, не успев начаться.
5 4 5 5 2 3
3 0 0 1 2
5 5 1 3 1 5
0 1 2 1 0
3 6 6 6
0 0 0
4 6 5 5 6
0 0 0 0
Организаторы CEOI 2011 собираются устроить вечеринку с кучей воздушных шариков. Всего будет \(n\) шариков (они все имеют форму идеального шара), и они будут лежать на одной линии на полу.
Шарики ещё не надуты, и каждый из них изначально имеет нулевой радиус. Ещё, \(i\)-й шар прикреплён к полу в позиции \(x_i\). Они будут надуваться последовательно, слева направо. Когда какой-то шарик надувается, его радиус непрерывно увеличивается, пока не достигнет верхней границы своего размера, \(r_i\), либо же не каснётся одного из уже надутых.
 Картинка 1: Шары из примера, после надувания.
Картинка 1: Шары из примера, после надувания.
Организваторы хотели бы оценить, сколько воздуха понадобится для надувания. Найдите, пожалуйста, итоговый радиус каждого шара.
В первой строке входных данных содержится целое число \(n\) (\(1\le n\le 200 000\)) – количество шаров.
Следующие \(n\) описывают шары. \(i\)-я из них содержит два целых числа \(x_i\) и \(r_i\) (\(0\le x_i\le 10^9\)), \(1\le r_i\le 10^9\)). Последовательность \(x_i\) строго возрастает.
Выведите \(n\) строк, в \(i\)-й строке должно быть единственное целое число – радиус \(i\)-го шара после надувания. Ваш ответ будет считаться верным, если он отличается от правильного не больше, чем на 0.001 в каждом числе.
1. (40 баллов) \(n\le 2000\).
2. (60 баллов) \(n\le 200000\).
3 0 9 8 1 13 7
9.000 1.000 4.694
Мислав и Мирко разработали новую игру под названием повороты.
Сначала Мирко выбирает последовательность чисел длины \(n\) и число \(k\) и разбивает последовательность на секции, каждая из которых содержит \(k\) чисел (\(n\) делится на \(k\)). Первая секция содержит первые \(k\) позиций в последовательности, вторая секция содержит последующие \(k\) позиций в последовательности и так далее.
После этого Мирко начинает применять различные операции на данной последовательности. Есть два типа операций:
1. Совершить циклический сдвиг элементов последовательности чисел в каждой секции на \(x\) влево или вправо.
2. Совершить циклический сдвиг элементов последовательности чисел целиком на \(x\) влево или вправо.
Заметим, что операция типа 2 может изменить то, к какой секции принадлежит какое число.
После применения всех операций, Мирко сообщает Миславу получившуюся последовательность и применённые операции. Задача Мислава заключается в том, чтобы восстановить исходную последовательность. Он попросил вас о помощи.
Первая строка ввода содержит три целых числа \(n\), \(k\), \(q\) (\(1 \le n \le 100000; 1 \le k \le 100000; 1 \le q \le 100000\)) - длину последовательности, длину каждой секции и количество применённых операций соответственно.
Последующие \(q\) строк содержат описание выполненных операций. Каждая из последующих \(q\) строк содержит два целых числа \(a\) (\(1 \le a \le 2\)) - тип операции, и \(x\) (\(-100000 \le x \le 100000\)) - число позиций, на которое был произведен циклический сдвиг. Если число \(x\) отрицательно, надо производить циклический сдвиг на \(|x|\) элементов влево, иначе - на \(|x|\) элементов вправо.
Последняя строка содержит \(n\) целых чисел, \(i\)-е из которых - это число, которое будет стоять на \(i\)-й позиции после выполнения операций из условия.
В единственной строке выведите \(n\) чисел - исходную последовательность.
Подзадача 1 (15 баллов): (\(n \le 100\))
Подзадача 2 (20 баллов): (\(k \le 100\))
Подзадача 3 (65 баллов): без дополнительных ограничений
4 2 2 2 2 1 1 3 2 1 0
0 1 2 3
8 4 4 1 3 1 15 1 -5 2 -1 6 10 14 19 2 16 17 1
6 10 14 1 2 16 17 19
9 3 5 1 1 2 -8 2 9 1 1 2 -4 3 1 8 7 4 5 2 6 9
5 3 6 9 7 1 8 2 4