Перебор с отсечением(22 задач)
Простые задачи на перебор(43 задач)
Гамильтонов цикл(2 задач)
Вывести все правильные скобочные выражения длиной \(N\), состоящие из круглых и квадратных скобок.
В первой строке находится единственное число \(N\). 1 <= \(N\) <= 14, \(N\) - чётное.
Каждое выражение выводится в отдельной строке, порядок вывода последовательностей произвольный.
2
() []
Дан набор переменных x1, x2, ..., xN. Каждая переменная xi может принимать значение только -1, 0 или +1. Для данного целого числа S требуется определить количество способов присвоить переменным xi значения так, чтобы сумма всех возможных произведений xi * xj была равна S, где i < j и i, j = 1, 2, ..., N. Два способа считаются различными, если они содержат различное число xi = 0.
Ограничения: 2 <= N <= 10 000, -10 000 < S < 10 000.
В первой строке находятся числа N и S, разделённые пробелом.
Вывести одно целое число - количество способов представить S как сумму произведений.
5 0
3
3 -2
0
На базаре есть ряд из N мест, где продаются семечки подсолнечника. Потенциальные покупатели идут вдоль ряда, затем в некоторый момент останавливаются и покупают семечки. Качество семечек от места к месту различается незначительно, так что разницы только в цене семечек и положении места.
Перед тем как выйти на рынок в качестве ещё одного продавца семечек, Вы провели исследование рынка, чтобы найти зависимость числа покупателей от двух названных факторов. Исследование показывает, что большинство покупателей следуют одному и тому же шаблону. Они проходят мимо нескольких мест, замечая и запоминая цены, а затем после обхода K мест, возвращаются к месту с наименьшей замеченной ценой, совершают там покупку, затем покидают базар. Если есть несколько мест с одинаковой ценой, покупатель выбирает ближайшее.
Предположим, что есть пять мест с ценами 37, 34, 34, 35, 33. Если покупатель с K = 4 идёт слева направо, он видит семечки по ценам 37, 34, 34, 35. В этот момент он решает, что видел достаточно, возвращается к третьему месту и покупает семечки там. Хотя на втором месте цена та же, что и на третьем, покупателю до него идти дальше. Если бы тот же покупатель зашёл справа, он бы увидел цены 33, 35, 34, 34, затем остановился и вернулся бы к пятому месту.
Число мест, пройденных до принятия решения (K), является функцией жадности и терпеливости покупателя, и, очевидно, различается у разных покупателей. Исследование выявило средний процент BK покупателей для всех значений K (1 <= K <= N, 0 <= BK <= 99, сумма всех BK равна 100).
Вам следует определить оптимальную стратегию на этом рынке (то есть цену и положение нового места, которое максимизирует ожидаемый средний доход) в предположении, что половина клиентов идёт в направлении от первого места к N-му, а другая половина - от N-го места к первому, и они следуют описанному шаблону.
В первой строке находится число существующих мест N, во второй строке - N целых чисел - цены на каждом месте, в третьей строке - N целых чисел в диапазоне от 0 до 99 - значения BK для каждого K. Все числа в строках разделены пробелами.
Ограничения: 2 <= N <= 100, исходные цены - целые числа от 1 до 9999.
Выводятся два целых числа - L и P. L (0 < L < N) - это число существующих мест, после которых должно быть размещено новое (Вам не разрешается устанавливать своё место первым или последним). Число P - оптимальная цена. Если существует более чем одно оптимальное решение, Вы должны выбрать решение с минимальным L, а среди них - с минимальным P.
3 1 11 11 33 34 33
2 10
На тропическом острове в разгар туристического сезона особой популярностью пользуется квас. Раньше весь квас импортировался из России, но с увеличением популярности этого напитка встал вопрос о производстве кваса прямо на месте. На острове расположено N курортных городов, все города расположены на побережье. Вдоль побережья проходит единственная на острове кольцевая дорога, соединяющая все города. Движение по дороге возможно в любом направлении. Для каждого города известно, сколько бочек кваса требуется ему ежедневно.
Планируется построить всего один завод в каком-нибудь городе, и развозить продукцию по остальным городам. Перевозка одной бочки в соседний город стоит один тугрик (местная валюта).
Ваша задача состоит в том, чтобы определить, в каком из городов следует построить завод, чтобы минимизировать транспортные расходы.
Первая строка входных данных содержит число N – количество городов ( N ≤ 10) и еще N чисел – количество кваса, требуемое ежедневно 1-м, 2-м, …, N -м городом (города нумеруются подряд вдоль кольцевой дороги).
Выведите одно число – номер города, в котором следует построить завод. Если подходящих городов окажется несколько – выведите номер любого из них.
 Примеры
Примеры
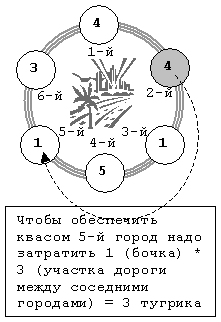
Пояснение для второго примера(см. рисунок):
На острове 6 городов, потребность каждого города указана в кружочках, номер города рядом с кружочком.
Если построить завод во 2-м городе (он выделен серым), то потребуется заплатить 4 + 1 (стоимость перевозки в 1-й и 3-й города) + 5*2 + 3*2 (в 4-й и 6-й) + 1*3 (в 5-й см. рисунок).
Во 2-й вообще ничего не везем. Это будет 24 тугрика. Легко проверить, что если построить завод в других городах, сумма будет больше. Например, если построить в 4-м городе, то сумма составит 1 + 1 + 3*2 + 4*2 + 4*3 = 28 тугриков.
3 5 3 10
3
6 4 4 1 5 1 3
2
Требуется расставить в некоторые клетки таблицы 3 x 3 крестики так, чтобы в каждой строке и в каждом столбце было заданное количество крестиков.
Вводятся 6 чисел (от 0 до 3) – требуемое количество крестиков в первом, втором, третьем столбце, в первой, второй, третьей строке.
Требуется выдать количество возможных таблиц или 0, если таких таблиц нет.
1 1 1 1 1 1
6
3 3 3 1 1 1
0