Перестановки(20 задач)
Сочетания(5 задач)
Разбиения(9 задач)
Разные комбинаторные структуры(17 задач)
Генерация по номеру(2 задач)
Совсем недавно появилась в продаже новая компьютерная игра «Морской бой—3». Вася купил себе эту игру и теперь играет в нее в свободное от занятий время. Особенно ему нравится в одной из миссий управлять самолетом. Изначально самолет находится на палубе неподвижного авианосца и готов в любой момент к взлету. Задача игрока в этой миссии состоит в уничтожении \(N\) кораблей противника. После уничтожения всех кораблей самолет должен вернуться обратно на авианосец.
Для простоты будем считать плоской поверхность моря, где располагается авианосец. Введем прямоугольную декартову систему координат и разместим авианосец в начале координат. Каждый из кораблей в начальный момент игры находится в некоторой точке (\(x\), \(y\)), и сразу после начала игры движется равномерно и прямолинейно так, что его вектор скорости равен (\(V_x\), \(V_y\)).
Конструктивные особенности самолета таковы, что он может двигаться с любой скоростью, не превосходящей \(U\). Для того, чтобы сбросить бомбу, которая была специально придумана для этой игры, самолету необходимо находиться непосредственно над кораблем. Корабли считаются точками, т.е. размером кораблей можно пренебречь. Считается также, что самолет может мгновенно взлететь с палубы авианосца, и время падения бомбы на цель равно нулю.
Требуется написать программу, определяющую минимальное время, за которое игрок сможет уничтожить все корабли и возвратить самолет обратно на авианосец.
Первая строка входного файла содержит число \(N\), определяющее количество кораблей (1 \(\le\) \(N\) \(\le\) 9). Вторая строка входного файла содержит целое число \(U\) (1 \(\le\) \(U\) \(\le\) 10000), задающее скорость самолета в метрах в секунду. Последующие \(N\) строк описывают все корабли. Каждая строка содержит четыре целых числа \(x\), \(y\), \(V_x\), \(V_y\), не превосходящих 10000 по модулю и определяющих начальные координаты и скорость корабля, соответственно. Координаты кораблей заданы в метрах, скорости — в метрах в секунду.
Гарантируется, что самолет летит быстрее, чем плывет любой из кораблей.
В первой строке выходного файла выведите минимальное время, требуемое на выполнение миссии. Требуемая точность — не менее \(10^{−3}\).
1 1000 10 10 0 0
0.0282842712474619
Разложение на простые множители числа \(12\) можно записать тремя способами:
\(\)12=2\cdot2\cdot3=2\cdot3\cdot2=3\cdot2\cdot2.\(\)
А сколькими способами можно записать разложение на простые множители числа \(N\)?
Вводится одно натуральное число \(N\) (\(2\le N\le 1 000\)).
Выведите одно число – количество различных записей разложения.
12
3
13
1
В тактике футбола одним из основных понятий является схема игры. Она определяет, сколько из десяти полевых игроков будут играть в защите, сколько — в полузащите и сколько — в нападении.
Например, схема игры 5-3-2 означает, что в команде пять защитников, три полузащитника и два нападающих. В соответствии с современными представлениями на схему игры накладываются следующие ограничения: должно быть не менее одного и не более пяти защитников, не менее одного и не более пяти полузащитников и не более трех нападающих. Отметим, что нападающих может в команде и не быть совсем. Будем рассматривать только такие схемы.
Будем считать, что футбольное поле имеет длину 120 метров и ширину 80 метров. Введем на нем прямоугольную декартову систему координат таким образом, как показано на рисунке. Ворота рассматриваемой нами команды находятся слева.
Будем также считать, что игрок в некоторый момент времени находится в линии полузащиты, если он находится на расстоянии не более 20 метров от центральной линии. Соответственно, игрок находится в линии защиты, если он находится не более чем в 40 метрах от «своей» лицевой линии, и в линии нападения, если находится не более чем в 40 метрах от «чужой» лицевой линии.
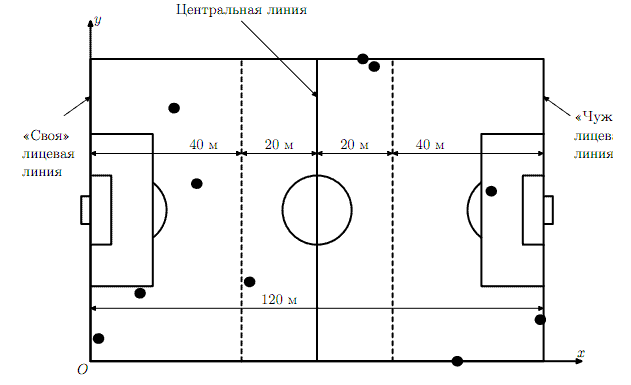
Например, в ситуации, изображенной на рисунке, в линии защиты находятся четыре игрока, в линии полузащиты — три, в линии нападения — также три.
В процессе игры некоторые игроки могут перемещаться из одной линии в другую. В этой задаче будем считать, что возможно перемещение из полузащиты в защиту (и обратно) и из полузащиты в нападение (и обратно). Таким образом, игрок, который в соответствии со схемой игры является защитником, не может оказаться в линии нападения, и наоборот — игрок, который в соответствии со схемой игры является нападающим, не может оказаться в линии защиты. Кроме этого, в соответствии с установкой тренера из каждой линии в каждую могло перейти не более двух игроков.
Ваша задача состоит в том, чтобы написать программу, которая по положениям игроков в некоторый момент времени найдет все возможные схемы игры, при которых в течение игры могло возникнуть такое расположение игроков.
Входной файл содержит десять строк, содержащих по два целых числа xi и yi каждая, — координаты каждого из игроков команды (0 ≤ xi ≤ 120, xi ≠ 40, xi ≠ 80, 0 ≤ yi ≤ 80).
В первой строке выходного файла выведите k — число схем игры, по которым может играть команда. В последующих k строках в произвольном порядке выведите описание каждой из этих схем. Следуйте формату данных, приведенному в примере.
97 0 13 18 2 6 119 11 42 21 72 80 75 78 106 45 22 67 28 47
9 2-5-3 3-5-2 3-4-3 4-5-1 4-4-2 4-3-3 5-4-1 5-3-2 5-2-3
Рассматриваются все разбиения натурального числа \(N\) на сумму \(К\) неотрицательных слагаемых (\(1 \leq N \leq 32\), \(2 \leq K \leq 32\)). Суммы, отличающиеся только порядком слагаемых, считаем различными. Упорядочим все разбиения по убыванию первого слагаемого, а при равных первых слагаемых – по убыванию второго слагаемого, а при равных первых и вторых слагаемых – по убыванию третьего слагаемого и т. д. Пронумеруем их. Например, при \(N=4\), \(К=3\) имеем:
| Номер | 1 слагаемое | 2 слагаемое | 3 слагаемое |
|---|---|---|---|
| 1 | 4 | 0 | 0 |
| 2 | 3 | 1 | 0 |
| 3 | 3 | 0 | 1 |
| 4 | 2 | 2 | 0 |
| 5 | 2 | 1 | 1 |
| 6 | 2 | 0 | 2 |
| 7 | 1 | 3 | 0 |
| 8 | 1 | 2 | 1 |
| 9 | 1 | 1 | 2 |
| 10 | 1 | 0 | 3 |
| 11 | 0 | 4 | 0 |
| 12 | 0 | 3 | 1 |
| 13 | 0 | 2 | 2 |
| 14 | 0 | 1 | 3 |
| 15 | 0 | 0 | 4 |
В первой строке входного файла записана последовательность чисел. Если первое число \(0\), то необходимо найти разбиение по номеру, а если \(1\), то номер по разбиению. В первом случае далее в файле записано количество слагаемых, сумма и номер разбиения. Во втором случае далее в файле записано количество слагаемых \(K\) и затем разбиение (\(K\) неотрицательных чисел, сумма которых \(N\)). Все числа разделены пробелами.
Выведите в выходной файл разбиение либо номер.
0 3 4 9
1 1 2
1 3 0 1 3
14