--->
177 задач
<---
Источники
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes
В первый день спортсмен пробежал \(x\) километров, а затем он каждый день увеличивал пробег на 70% от предыдущего значения. По данному числу \(y\) определите номер дня, на который пробег спортсмена составит не менее \(y\) километров.
Входные данные
На вход программа получает два действительных числа \(x\) и \(y\) . Числа положительные, действительные, не превосходят 1000, заданы с точностью до шести знаков после запятой.
Выходные данные
Программа должна вывести единственное целое число.
Примеры
Входные данные
10 30
Выходные данные
4
Входные данные
10 50
Выходные данные
5
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes
В первый день спортсмен пробежал \(x\) километров, а затем он каждый день увеличивал пробег на 70% от предыдущего значения. По данному числу \(y\) определите номер дня, на который суммарный пробег спортсмена составит не менее \(y\) километров.
Входные данные
На вход программа получает два действительных числа \(x\) и \(y\) . Числа положительные, действительные, не превосходят 1000, заданы с точностью до шести знаков после запятой.
Внимание! В некоторых тестах оба числа находятся на одной строке, а в некоторых — на разных!
Выходные данные
Программа должна вывести единственное целое число.
Примеры
Входные данные
1 20
Выходные данные
6
#773
Темы:
[Цикл for]
Источники:
[
Командные олимпиады,
Школьная командная олимпиада ФМШ № 2007 г.Москвы,
8-9 классы,
2007-2008,
Задача A
]
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes
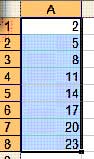Если в Microsoft Excel выделить две соседние клетки с числами, а потом “потянуть” за правый нижний уголок мышью, то следующие клетки заполнятся числами, образуя арифметическую прогрессию.
Входные данные
Вводятся сначала два натуральных числа, по модулю не превышающие 100 – числа в первых двух клетках, а затем число N (натуральное, 2 ≤ N ≤ 100) – общее количество чисел в арифметической прогрессии (включая два первых числа). Числа вводятся через пробел.
Выходные данные
Выведите N членов арифметической прогрессии, разделяя их пробелом.
Примеры
Входные данные
2 5 8
Выходные данные
2 5 8 11 14 17 20 23
#777
Темы:
[Цикл for]
Источники:
[
Командные олимпиады,
Школьная командная олимпиада ФМШ № 2007 г.Москвы,
8-9 классы,
2007-2008,
Задача E
]
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes
Колоду карт раздают по кругу, по одной карте каждому за раз, пока колода не кончится. Известен порядок карт в колоде. С кого должен начинать сдающий, чтобы первый игрок получил себе как можно больше тузов?
Входные данные
В первой строке вводятся два числа: количество игроков и количество карт в колоде (оба числа натуральные и не превосходят 100, количество карт делится на количество игроков).
Во второй строке через пробел перечислены достоинства карт в том порядке, в котором они идут в колоде (6 – шестерка, 7 – семерка, 8 – восьмерка, 9 – девятка, 10 – десятка, 11 – валет, 12 – дама, 13 – король, 14 – туз). В колоде может быть произвольное число карт каждого достоинства.
Выходные данные
Выведите одно число – номер игрока, с которого следует начинать сдавать, чтобы первый игрок получил как можно больше тузов (игроки нумеруются числами 1, 2, 3, ...; сдача происходит по возрастанию номеров начиная с некоторого до последнего, и затем продолжается с первого). Если вариантов ответа несколько, выведите любой из них.
Примеры
Входные данные
5 10 9 9 9 14 8 7 11 6 14 6
Выходные данные
3
Входные данные
3 3 14 14 14
Выходные данные
1
#792
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes
Вводится натуральное число. Требуется разделить запятыми тройки его цифр (считая справа).
Входные данные
Вводится одно натуральное число, не превышающее 10100.
Выходные данные
Вывести то же число, разделяя тройки цифр запятыми.
Примеры
Входные данные
1000
Выходные данные
1,000
Входные данные
12345678
Выходные данные
12,345,678
Входные данные
999
Выходные данные
999
Выбрано
:
|