--->
102 задач
<---
Источники
В некоторой сверхсекретной лаборатории изучаются физические возможности животных. Любой живой организм нуждается в трех компонентах пищи – белках, жирах и углеводах. Известен набор продуктов, имеющийся в распоряжении лаборатории, и меню животных – сколько единиц каждого продукта они получают. Известно также, сколько белков, жиров и углеводов необходимо для нормальной жизнедеятельности животного. Необходимо определить, получает ли животное достаточное количество питательных веществ. Известно, что животному требуется в сутки \(X\) белков, \(Y\) жиров и \(Z\) углеводов.
Известно также, что всего животное получает в сутки \(N\) продуктов питания, и для каждого из них известны \(A_i\), \(B_i\), \(C_i\) и \(Q_i\) – соответственно, энергетическая ценность единицы продукта в белках, жирах и углеводах и количество единиц этого продукта. Все числа – действительные, заданные с точностью до 5 знаков после запятой.
Входные данные
На первой строке входных данных записаны числа \(X\) , \(Y\) и \(Z\) . На второй строке записано число \(N\). Далее на \(N\) строках записаны, соответственно, \(A_i\), \(B_i\), \(C_i\) и \(Q_i\).
Выходные данные
Выведите YES , если данный пищевой рацион является достаточным по всем параметрам, и NO в противном случае.
Примеры
Входные данные
1.0 1.0 1.0 3 1 0 0 1 0 0.5 0 2 0 0 0.25 4
Выходные данные
YES
#773
Темы:
[Цикл for]
Источники:
[
Командные олимпиады,
Школьная командная олимпиада ФМШ № 2007 г.Москвы,
8-9 классы,
2007-2008,
Задача A
]
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes
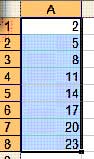Если в Microsoft Excel выделить две соседние клетки с числами, а потом “потянуть” за правый нижний уголок мышью, то следующие клетки заполнятся числами, образуя арифметическую прогрессию.
Входные данные
Вводятся сначала два натуральных числа, по модулю не превышающие 100 – числа в первых двух клетках, а затем число N (натуральное, 2 ≤ N ≤ 100) – общее количество чисел в арифметической прогрессии (включая два первых числа). Числа вводятся через пробел.
Выходные данные
Выведите N членов арифметической прогрессии, разделяя их пробелом.
Примеры
Входные данные
2 5 8
Выходные данные
2 5 8 11 14 17 20 23
#777
Темы:
[Цикл for]
Источники:
[
Командные олимпиады,
Школьная командная олимпиада ФМШ № 2007 г.Москвы,
8-9 классы,
2007-2008,
Задача E
]
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes
Колоду карт раздают по кругу, по одной карте каждому за раз, пока колода не кончится. Известен порядок карт в колоде. С кого должен начинать сдающий, чтобы первый игрок получил себе как можно больше тузов?
Входные данные
В первой строке вводятся два числа: количество игроков и количество карт в колоде (оба числа натуральные и не превосходят 100, количество карт делится на количество игроков).
Во второй строке через пробел перечислены достоинства карт в том порядке, в котором они идут в колоде (6 – шестерка, 7 – семерка, 8 – восьмерка, 9 – девятка, 10 – десятка, 11 – валет, 12 – дама, 13 – король, 14 – туз). В колоде может быть произвольное число карт каждого достоинства.
Выходные данные
Выведите одно число – номер игрока, с которого следует начинать сдавать, чтобы первый игрок получил как можно больше тузов (игроки нумеруются числами 1, 2, 3, ...; сдача происходит по возрастанию номеров начиная с некоторого до последнего, и затем продолжается с первого). Если вариантов ответа несколько, выведите любой из них.
Примеры
Входные данные
5 10 9 9 9 14 8 7 11 6 14 6
Выходные данные
3
Входные данные
3 3 14 14 14
Выходные данные
1
#792
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes
Вводится натуральное число. Требуется разделить запятыми тройки его цифр (считая справа).
Входные данные
Вводится одно натуральное число, не превышающее 10100.
Выходные данные
Вывести то же число, разделяя тройки цифр запятыми.
Примеры
Входные данные
1000
Выходные данные
1,000
Входные данные
12345678
Выходные данные
12,345,678
Входные данные
999
Выходные данные
999
#846
Темы:
[Цикл for]
[Целые числа]
Вместо того чтобы делать уроки, Петя смотрел футбольный матч и записывал счет, который показывался на табло, после каждого забитого гола.
Например, у него могла получиться такая запись:
1:0
1:1
1:2
2:2
2:3
После этого он сложил все записанные числа: 1+0+1+1+1+2+2+2+2+3=15.
По сумме, получившейся у Васи, определите, сколько всего мячей было забито в матче.
Входные данные
Вводится одно натуральное число, не превосходящее 1000 – сумма, полученная Васей.
Выходные данные
Выведите одно число – общее количество забитых мячей.
Примеры
Входные данные
3
Выходные данные
2
Входные данные
1
Выходные данные
1
Выбрано
:
|