Темы --> Информатика --> Алгоритмы --> Перебор --> Комбинаторные структуры --> Разные комбинаторные структуры
---> 17 задач <---
Источники
    Личные олимпиады(938 задач)
    Командные олимпиады(684 задач)
Страница: << 1 2 3 4 >> Отображать по:
#1050
Фигурное программирование
  
#1114
Оптимизация
  
Источники: [ Командные олимпиады, ВКОШП, 2008, Задача G ]
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
256 megabytes

В компании QQQ работает n человек. Очередной проект компании состоит из m независимых частей. Управляющий компании оценил время, которое требуется для выполнения каждой из частей проекта (предполагается, что это время не зависит от того, кто будет выполнять эту часть). После чего он некоторым образом распределил все m частей между n работниками. В результате оказалось, что некоторым из работников потребуется потратить на выполнение своей работы больше времени, чем другим (поскольку им досталась более объемная работа).

Поэтому управляющий решил улучшить распределение работ следующим образом: выбрать двух различных работников и выбрать одну из частей проекта, назначенную первому работнику, и одну из частей, назначенную второму. После этого часть проекта, назначенную первому работнику, назначить второму, а часть, назначенную второму, назначить первому. Если в результате этой операции максимум из времен выполнения работы первым и вторым работниками уменьшился, то такую операцию назовем оптимизирующей.

Например, пусть проект состоит из пяти частей со временами выполнения 3,6,4,8,2, и в компании есть три работника. Пусть распределение работ выглядит следующим образом: первый работник части 1 и 2 (суммарное время 3 + 6 = 9), второй работник часть 4 (суммарное время 8) и третий работник части 3 и 5 (суммарное время 4 + 2 = 6). Тогда если первое задание (назначенное первому работнику) назначить третьему, а пятое задание (назначенное третьему) назначить первому, то у первого работника суммарное время станет равно 6 + 2 = 8, а у третьего 3 + 4 = 7. Поскольку max(9,6) > max(8,7), то эта операция будет оптимизирующей.

Вам дано число работников в компании, число частей в проекте, время, необходимое на выполнение каждой из частей проекта и распределение частей по работникам. Требуется посчитать число различных возможных оптимизирующих операций в данном распределении работ.

Входные данные

Первая строка входного файла содержит два натуральных числа n и m (1 ≤ n,m ≤ 105) число работников в компании и число частей в проекте соответственно. Вторая строка содержит m натуральных чисел i-ое число равно времени выполнения i-ой части проекта (части проекта нумеруются, начиная с 1). Времена выполнения частей не превосходят 109. Далее идут n строк, описывающих распределение частей по работникам. Каждая строка содержит описание частей проекта, которые получил соответствующий работник. Описание состоит из числа частей, которые достались работнику, и их номеров.

Выходные данные

В выходной файл выведите искомое число оптимизирующих операций.

Примеры
Входные данные
3 5
3 6 4 8 2
2 1 2
1 4
2 3 5
Выходные данные
2
Входные данные
5 13
1 2 7 5 8 7 5 4 1 5 1 5 7
3 1 2 3
2 4 5
2 6 7
3 8 9 10
3 11 12 13
Выходные данные
5
#1136
Азбука для слепых
  
Требуется определить количество вариантов заполнить таблицу черными и белыми клетками так, чтобы одна фигура не получалась из другой с помощью сдвига.

Известно, что в книгах для слепых для обозначения различных букв используются различные комбинации выступов, которые читающий различает на ощупь. Пусть для обозначения буквы используется прямоугольник шириной M мм и высотой N мм, причем некоторые входящие в него квадратики размера 1∙1 содержат выступ.

Поскольку слепой не видит границ прямоугольника, то он не может различить комбинации, получающиеся друг из друга сдвигом. Так, он не может различить комбинации а) и б) на рисунке 1. (В то же время комбинации а) и в) являются различимыми, поскольку не могут быть получены друг из друга сдвигом)

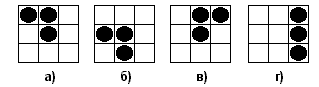
Рисунок 1.

Из-за этого при разработке алфавита для слепых появилась проблема: сколько различных букв можно представить с помощью выступов, если запрещается сопоставлять различным буквам комбинации, получающиеся друг из друга сдвигом. Прямоугольник совсем без выступов также нельзя использовать в качестве буквы (поскольку при написании слова между некоторыми буквами может появиться такой прямоугольник, например между а) и г) на рисунке 1).

Требуется подсчитать количество различных букв, которые можно представить таким способом, если прямоугольник имеет размер M∙N.

В качестве примера, все буквы размера 2∙2 приведены на рисунке 2. (Среди комбинаций, отвечающих одной букве, приведена только одна)

Рисунок 2.

Входные данные

Входной файл содержит числа M и N, разделенный пробелом. Поскольку человек одновременно не может воспринимать слишком много информации, M∙N ≤ 30.

Выходные данные

Выведите в выходной файл единственное число – количество различных букв, которые слепой сможет различить при заданном размере прямоугольника.

Примеры
Входные данные
2 3
Выходные данные
44
#1618
Кодовый замок
  
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes

Кодовый замок состоит из \(N\) рычажков, каждый из которых может быть установлен в любое из \(K\) положений, обозначенных натуральными числами от 1 до \(K\). Известно, что для того чтобы открыть замок, нужно, чтобы сумма положений любых трех последовательных рычажков была равна \(K\).

Два рычажка уже установлены в некоторые положения, и их переключать нельзя. Рычажок с номером \(p_1\) установлен в положение \(v_1\), а рычажок \(p_2\) – в положение \(v_2\).

Напишите программу, которая определит, сколькими способами можно установить остальные рычажки, чтобы открыть замок.

Входные данные

Вводятся натуральные числа \(N\), \(K\), \(p_1\), \(v_1\), \(p_2\), \(v_2\). 3 ≤ \(N\) ≤ 100 000, 3 ≤ \(K\) ≤ 100 000, \(p_1\) ≠ \(p_2\), 1 ≤ \(p_1\) ≤ \(N\), 1 ≤ \(p_2\) ≤ \(N\), 1 ≤ \(v_1\) ≤ \(K\), 1 ≤ \(v_2\) ≤ \(K\).

Выходные данные

Выведите одно число — количество искомых комбинаций или 0, если, соблюдая все условия, замок открыть невозможно.

Примеры
Входные данные
3 3 1 1 2 1
Выходные данные
1
Входные данные
3 3 1 1 3 2
Выходные данные
0
#1628
Кодовый замок
  
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes

Кодовый замок состоит из \(N\) рычажков, каждый из которых может быть установлен в любое из \(K\) положений, обозначенных натуральными числами от 1 до \(K\). Известно, что для того чтобы открыть замок, нужно, чтобы сумма положений любых трех последовательных рычажков была равна \(K\).

Два рычажка уже установлены в некоторые положения, и их переключать нельзя. Рычажок с номером \(p_1\) установлен в положение \(v_1\), а рычажок \(p_2\) – в положение \(v_2\).

Напишите программу, которая определит, сколькими способами можно установить остальные рычажки, чтобы открыть замок.

Входные данные

Вводятся натуральные числа \(N\), \(K\), \(p_1\), \(v_1\), \(p_2\), \(v_2\). Рычажки пронумерованы числами от 1 до \(N\).

3 ≤ \(N\) ≤ 10000, 3 ≤ \(K\) ≤ 6, \(p_1\)≠\(p_2\), 1 ≤ \(p_1\) ≤ \(N\), 1 ≤ \(p_2\) ≤ \(N\), 1 ≤ \(v_1\) ≤ \(K\), 1 ≤ \(v_2\) ≤ \(K\).

Выходные данные

Выведите одно число — количество искомых комбинаций или 0, если, соблюдая все условия, замок открыть невозможно.

Страница: << 1 2 3 4 >> Отображать по:
Выбрано
:
Отменить
|
Добавить в контест