Вова и Марина любят играть в игры, а особенно — придумывать к ним свои правила. Недавно они открыли для себя веселую игру «Чапаев», в которой игроки должны сбивать щелчками шашки вражеского цвета с шахматной доски (также эта игра известна под названием «Щелкунчики»). Вдоволь наигравшись, они решили модифицировать правила, добавив игре математическую сложность.
Теперь они играют в «Чапаева» не на шахматной доске, а на доске в форме дерева! Их дерево состоит из \(N\) вершин. Вершина 1 является корнем дерева, а из каждой из оставшихся вершин проведено ребро в некоторую вершину с меньшим номером — ее непосредственного предка.
В игре участвуют шашки одного цвета, изначально расположенные в некоторых вершинах дерева. За один ход игрок выбирает некоторую шашку и щелчком отправляет ее к корню по ребрам дерева, сбивая при этом с доски все встреченные на пути шашки. Сама шашка, по которой производился удар, после попадания в корень дерева также слетает с доски.
Игроки делают ходы по очереди. Проигрывает тот игрок, к ходу которого на доске не остается шашек.
Придуманная ими игра замечательна также тем, что на одной и той же доске можно играть, начиная с разных начальных позиций шашек. Практика показала, что самые интересные партии получаются, если исходно расставить фишки во все вершины, являющиеся потомками (непосредственными или косвенными) некоторой вершины Root, при этом в саму вершину Root фишка не ставится.
Дети решили сыграть \(N\) партий, перебрав в качестве вершины Root каждую вершину дерева по одному разу. Если у очередной вершины Root нет потомков, и на доске исходно не оказывается ни одной фишки, то игры не происходит, и дети переходят к следующей расстановке. В каждой партии Марина ходит первой.
Вова интересуется у вас, в скольких партиях Марина сможет одержать победу, если игроки будут действовать оптимально.
В первой строке находится целое число \(N\) (1 ≤ \(N\) ≤ 500 000) — количество вершин в дереве.
Во второй строке следуют целые числа \(p_2\), \(p_3\), ..., \(p_N\), разделенные пробелами, где \(p_i\) — это номер вершины, являющейся предком вершины \(i\) (1 ≤ pi < i).
Выведите единственное целое число — количество партий, в которых Марина одержит победу.
Разберем тест из условия. Доска для игры показана на рисунках ниже. Дети сыграют четыре партии, выбирая в качестве Root вершины 1, 2, 3 и 5. Если выбрать в качестве Root любую из трех оставшихся вершин, на доске исходно не окажется ни одной фишки, поэтому игры не произойдет.
Если выбрать в качестве Root вершину 5, фишки будут исходно находиться в вершинах 6 и 7. В такой партии Марина проигрывает: после того, как она сбивает любую из этих двух фишек с доски, Вова сбивает оставшуюся и заканчивает партию.
Если выбрать в качестве Root вершину 2 или 3, у Марины будет возможность выиграть игру за один ход, щелкнув по фишке из вершины 4 (при этом, в случае Root = 2, она по пути также собьет фишку из 3 вершины по правилам игры)
Можно убедиться, что если выбрать в качестве Root вершину 1, у Марины также будет выигрышная стратегия. Для этого первым ходом Марина должна сбить фишку из вершины 2. Пример партии с таким начальным расположением показан ниже.
Таким образом, Марина выигрывает в трех партиях
Тесты к этой задаче состоят из пяти групп. Баллы за каждую группу ставятся только при прохождении всех тестов группы и всех тестов предыдущих групп.
0. Тест 1. Тест из условия, оценивается в ноль баллов.
1. Тесты 2–17. В тестах этой группы \(N\) ≤ 20. Эта группа оценивается в 20 баллов
2. Тесты 18–38. В тестах этой группы \(N\) ≤ 200. Эта группа оценивается в 20 баллов.
3. Тесты 39–59. В тестах этой группы \(N\) ≤ 5 000. Эта группа оценивается в 20 баллов.
4. В тестах этой группы дополнительные ограничения отсутствуют. Эта группа оценивается в 40 баллов.
7 1 2 3 1 5 5
3
Как-то раз, разбирая вещи на чердаке, Петя нашел странную игру. В начале игры на поле выкладываются карточки с числами. Затем двое игроков по очереди берут себе по одной карте за ход. Игра заканчивается, когда на поле не остается карточек. Выигрывает тот, у кого сумма чисел на карточках делится на три. В случае если сумма чисел делится на три у обоих игроков, объявляется ничья. Также ничья объявляется, если ни у одного игрока сумма не делится на три.
Петя выяснил, что эта игра была довольно популярна когда-то, и что у некоторых его друзей она тоже есть. Единственное отличие состоит в том, что набор карт у всех разный.
Теперь Пете интересно, каков будет исход партии при оптимальной игре. Помогите ему выяснить это.
Первая строка входного файла содержит натуральное число n — количество карточек ( 1 ≤ n ≤ 50 ). Следующая строка содержит n целых чисел, разделенных пробелами — значения, написанные на карточках. Все числа во входном файле не превосходят 1000 по модулю.
В первой строке выходного файла выведите «FIRST», если при оптимальной игре выигрывает первый игрок, «SECOND», если второй. В случае, если при оптимальной игре случается ничья, выведите «DRAW».
2 1 3
FIRST
3 3 6 9
DRAW
В двусвязном списке, он же LinkedList, каждый элемент может быть связан максимум с двумя другими элементами — с предыдущим элементом (если он есть) и со следующим элементом (если он есть).
Билли и Рикардо проходят стажировку в компании FlexDex в группе поддержки внутреннего анонимного форума с возможностью деанонимизации. Для представления последовательных сообщений в теме необходимо использовать список, где элементами будут являться эти сообщения, и два товарища решили написать свою быструю реализацию двусвязного списка FlexList.
Но у них что-то пошло не так — в их списке новое сообщение может связываться не только с первым или последним сообщением, как должно быть, а с любым из уже существующих сообщений.
Если представить каждое сообщение как вершину графа, а связи между сообщениями как ребра графа, то гарантируется, что этот граф будет неориентированным, связным и ацикличным.
Говорится, что граф является корректным графом, если в этом графе у каждой вершины не более двух вершин, связанных с ней ребром. Изначально же FlexList связи между сообщениями могут выглядеть в виде любого связного ацикличного графа, не обязательно корректного.
Билли и Рикардо не растерялись и решили, что будут вручную исправлять все неясности в ходе работы программ, которые используют их изобретение. Тимлид дал им тестовый пример для проверки кода. Они получили на этом примере граф связей и вручную делают из него корректный граф, ведь связи между сообщениями в корректном двусвязном списке могут представлять собой только корректный граф.
Это выглядит так — сначала Билли проверяет, что граф корректный. Если это не так, то он выбирает и удаляет некоторый лист (вершина, у которой есть ровно одна связь с другими вершинами), и отдает граф Рикардо, затем Рикардо делает то же самое и отдает граф Билли, и так продолжается до тех пор, пока кто-то не получит от товарища корректный граф. Как только один из двух друзей получает такой граф, то тут же показывает его тимлиду, с надеждой на похвалу и повышение в должности.
Каждый хочет получить первым такой граф. Кто первым попадет к тимлиду, если оба товарища удаляют листья оптимально для себя?
В первой строке содержится одно целое число \(n\) (\(1 \leq n \leq 300\,000\)) — число сообщений в примере тимлида. Следующие \(n - 1\) строк задают связи между сообщениями. Каждая из них содержит два целых числа \(a_i\) и \(b_i\) (\(1 \leq a_i, b_i \leq n\), \(a_i \neq b_i\)), которые показывают, что сообщения с номерами \(a_i\) и \(b_i\) связаны.
Выведите "Billy" (без кавычек), если первым попадет к тимлиду Билли, иначе выведите "Ricardo" (без кавычек).
В первом примере Билли первым ходом может удалить одну из вершин с номерами \(2\), \(4\) или \(5\), так как они являются листьями. Он не будет удалять вершину с номером \(4\) или \(5\), так как в таком случае он передаст Рикардо корректный граф и проиграет. Значит, он удалит вершину \(2\). В свою очередь, Рикардо может удалить вершины \(1\), \(4\) или \(5\), и, в любом случае, Билли получит от него корректный граф.
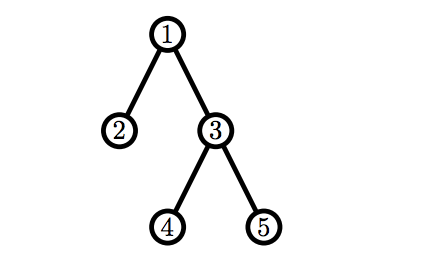
Во втором примере у Билли сразу есть корректный граф.
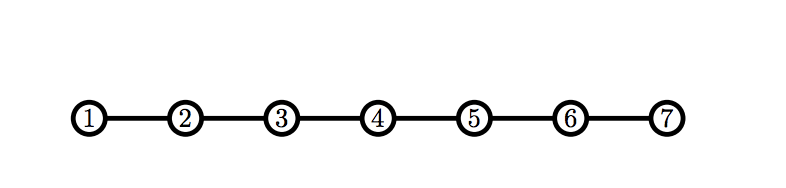
В третьем примере можно показать, что вне зависимости от ходов Билли, Рикардо получит корректный граф первым.
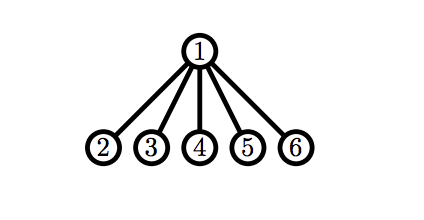
5 1 2 1 3 3 4 3 5
Billy
7 1 2 2 3 3 4 4 5 5 6 6 7
Billy
6 1 2 1 3 1 4 1 5 1 6
Ricardo