Двое друзей играют в игру на бесконечной ленте. У каждого из них есть по одной фишке. В начале игры обе фишки стоят на первой клетке. Кроме этого, есть набор карточек с числами.
Игра состоит в том, что игроки по очереди выбирают одну из карточек и передвигают свою фишку по ленте на то количество клеток, какое число написано на карточке. После этого карточка выбрасывается.
Игра завершается, когда карточки закончились. Победившим считается игрок, у которого фишка стоит на поле с большим номером.
Известен набор карточек. Напишите программу, которая определит победителя и номера клеток, на которых будут стоять фишки по окончанию игры. Известно, что оба друга играют по оптимальной стратегии.
Сначала вводится число \(N\) — количество карточек с числами (1≤\(N\)≤100000). Далее записаны \(N\) натуральных чисел — числа, написанные на карточках. Каждое из этих чисел не превышает 10000.
Выведите номер клетки, на которой будет стоять в конце игры фишка победителя, и номер клетки, на которой будет стоять фишка его противника, если оба использовали оптимальную стратегию.
4 5 1 8 2
11 7
5 9 6 3 7 10
21 16
На планете Шелезяка катастрофа — запасы смазки подходят в концу. В связи с этим правительство решило организовать всепланетное соревнование, главный приз в котором — вагон смазочных материалов.
Соревнование проводится в несколько этапов, каждый из которых поделен на множество раундов. В каждом раунде принимают участие два игрока. Жюри предоставляет им большое целое число \(n\). Затем игроки делают ходы по очереди. Первый ход первого игрока заключается в том, что игрок выписывает на специальном поле цифру, причем первым ходом запрещается выписывать ноль. В дальнейшем ход игрока заключается в том, что он приписывает справа к уже написанному числу произвольную цифру. Выигрывает тот, после чьего хода выписанное число больше или равно \(n\).
Знаменитый ученый-робот «ЩК-33» считает, что результат игры легко предсказуем. Для доказательства он решил предоставить программу, которая определяет, кто выигрывает, если оба игрока действуют по оптимальной стратегии. К сожалению, из-за недостатка смазки, его манипуляторы вышли из строя, поэтому он просит вас о помощи.
Первая строка входного файла содержит целое число \(n\) (\(1 \le n \le 10^{100\,000}\)). Это число не содержит ведущих нулей.
Выведите «First», если при оптимальной игре выигрывает первый игрок, и «Second» в противном случае.
22
First
1
First
На листке записано в одну строку \(N\) (\(2 \leq N \leq 100\)) целых положительных чисел. Каждое число не превышает 200. Играют двое. За каждый ход можно зачеркивать крайнее число либо слева, либо справа. Зачеркнутое число добавляется к очкам игрока. \(N\) – четное. Игру начинает первый игрок. Необходимо вывести максимально возможную сумму очков для первого игрока при условии, что противник играет наилучшим образом..
В первой строке входного файла содержится одно целое число \(N\) (\(2 \leq N \leq 100\)). В следующих \(N\) строках записан исходный ряд чисел, по одному числу в строке.
Выходной файл должен содержать единственное число – максимально возможную сумму очков для первого игрока при наилучшей игре второго игрока.
6 4 7 2 9 5 2
18
Петя с Андреем играют в интересную игру. Для этой игры им необходимо k шоколадок, каждая из которых имеет форму прямоугольника i-ая из них имеет размер wi на hi долек.
Петя с Андреем ходят по очереди, за один ход игрок должен взять со стола одну шоколадку, разломать ее на две неравных непустых части, и их обе положить обратно на стол. При этом обе получающиеся части должны иметь форму прямоугольника, длины сторон которого выражаются целым числом долек.
Первый ход в этой игре делает Петя. Проигрывает игрок, который не может сделать ход. Победитель после этого получает весь шоколад, лежащий на столе.
Ваша задача — определить, кто из игроков выиграет при оптимальной игре обоих.
Входной файл содержит несколько наборов входных данных. Первая строка входного файла содержит количество T наборов входных данных (1 ≤ T ≤ 1000).
Каждый набор входных данных описывается следующим образом. Первая строка описания содержит число k (1 ≤ k ≤ 100) — количество шоколадок, лежащих на столе в начале игры. Последующие k строк описывают шоколадки: i-ая из этих строк содержит два числа: wi и hi — размеры соответствующей шоколадки (1 ≤ wi, hi ≤ 100).
Для каждого набора входных данных выведите ответ. Следуйте формату, приведенному в примерах.
3 1 1 1 1 3 1 2 1 1 3 1
Game 1: Andrew wins. Game 2: Petr wins. Game 3: Petr wins.
В двусвязном списке, он же LinkedList, каждый элемент может быть связан максимум с двумя другими элементами — с предыдущим элементом (если он есть) и со следующим элементом (если он есть).
Билли и Рикардо проходят стажировку в компании FlexDex в группе поддержки внутреннего анонимного форума с возможностью деанонимизации. Для представления последовательных сообщений в теме необходимо использовать список, где элементами будут являться эти сообщения, и два товарища решили написать свою быструю реализацию двусвязного списка FlexList.
Но у них что-то пошло не так — в их списке новое сообщение может связываться не только с первым или последним сообщением, как должно быть, а с любым из уже существующих сообщений.
Если представить каждое сообщение как вершину графа, а связи между сообщениями как ребра графа, то гарантируется, что этот граф будет неориентированным, связным и ацикличным.
Говорится, что граф является корректным графом, если в этом графе у каждой вершины не более двух вершин, связанных с ней ребром. Изначально же FlexList связи между сообщениями могут выглядеть в виде любого связного ацикличного графа, не обязательно корректного.
Билли и Рикардо не растерялись и решили, что будут вручную исправлять все неясности в ходе работы программ, которые используют их изобретение. Тимлид дал им тестовый пример для проверки кода. Они получили на этом примере граф связей и вручную делают из него корректный граф, ведь связи между сообщениями в корректном двусвязном списке могут представлять собой только корректный граф.
Это выглядит так — сначала Билли проверяет, что граф корректный. Если это не так, то он выбирает и удаляет некоторый лист (вершина, у которой есть ровно одна связь с другими вершинами), и отдает граф Рикардо, затем Рикардо делает то же самое и отдает граф Билли, и так продолжается до тех пор, пока кто-то не получит от товарища корректный граф. Как только один из двух друзей получает такой граф, то тут же показывает его тимлиду, с надеждой на похвалу и повышение в должности.
Каждый хочет получить первым такой граф. Кто первым попадет к тимлиду, если оба товарища удаляют листья оптимально для себя?
В первой строке содержится одно целое число \(n\) (\(1 \leq n \leq 300\,000\)) — число сообщений в примере тимлида. Следующие \(n - 1\) строк задают связи между сообщениями. Каждая из них содержит два целых числа \(a_i\) и \(b_i\) (\(1 \leq a_i, b_i \leq n\), \(a_i \neq b_i\)), которые показывают, что сообщения с номерами \(a_i\) и \(b_i\) связаны.
Выведите "Billy" (без кавычек), если первым попадет к тимлиду Билли, иначе выведите "Ricardo" (без кавычек).
В первом примере Билли первым ходом может удалить одну из вершин с номерами \(2\), \(4\) или \(5\), так как они являются листьями. Он не будет удалять вершину с номером \(4\) или \(5\), так как в таком случае он передаст Рикардо корректный граф и проиграет. Значит, он удалит вершину \(2\). В свою очередь, Рикардо может удалить вершины \(1\), \(4\) или \(5\), и, в любом случае, Билли получит от него корректный граф.
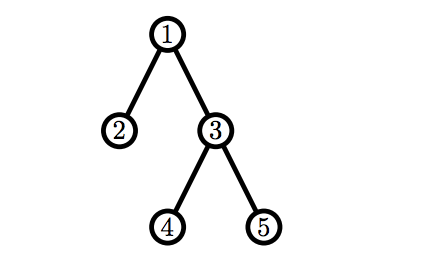
Во втором примере у Билли сразу есть корректный граф.
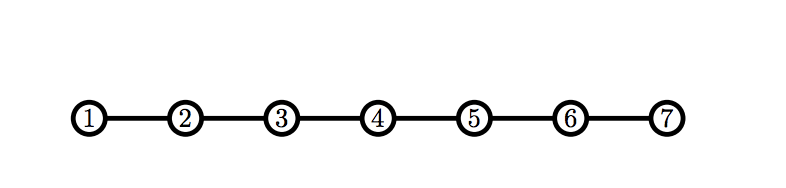
В третьем примере можно показать, что вне зависимости от ходов Билли, Рикардо получит корректный граф первым.
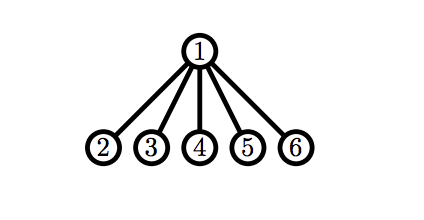
5 1 2 1 3 3 4 3 5
Billy
7 1 2 2 3 3 4 4 5 5 6 6 7
Billy
6 1 2 1 3 1 4 1 5 1 6
Ricardo