Страница: << 18 19 20 21 22 23 24 >> Отображать по:
#2858
Лестница
  
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes

Археологи раскопали Древний Храм, ко входу в который ведет лестница, шириной в 1 (один) метр, из М ступенек различной длины и высоты. Лестница построена из каменных блоков 1x1x1 метр. Археологи хотят для удобства туристов, чтобы лестница состояла из меньшего количества ступенек N. Для этого они могут также устанавливать каменные блоки 1x1x1. Какое минимальное количество блоков необходимо, чтобы сделать лестницу в N ступенек, если известны начальная длина и высота каждой ступеньки. Высоты и длины ступенек новой лестницы могут различаться.

Входные данные

В первой строке через пробел заданы два целых числа M и N (1 ≤ N < M ≤ 100). Далее идут M строк, содержащих пару целых чисел L и H - длина и высота i-ой ступеньки соответственно (1 ≤ L, H ≤ 101). Ступеньки нумеруются снизу вверх.

Выходные данные

В выходной файл выведите единственное число - ответ на задачу.

Примеры
Входные данные
5 3
4 2
1 2
5 2
1 2
2 1
Выходные данные
3
#2883
Swimming pool
  
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
256 megabytes

В бассейне плавает \(S\) людей.

В какой-то момент тренер обратил внимание на неравномерное распределение людей по дорожкам бассейна, что вызывает неудобство у посетителей. Для хорошего распределения пловцов необходимо, чтобы их количество на соседних дорожках отличалось не более чем на 1. Но каждое пересечение разделительных поплавков между дорожками увеличивает дискомфорт пловцов. Например, пустая дорожка может быть рядом с пустой или с дорожкой на которой только один пловец.

Ваша задача состоит в том, чтобы минимизировать дискомфорт, возникающий при перемещении с дорожки на дорожку и добиться хорошего распределения посетителей в бассейне.

Входные данные

Первая строка содержит единственное целое число \(N\) – количество дорожек \((1 \le N \le 400)\). Следующая строчка содержит \(N\) чисел, разделённых пробелами. \(i\)-ое число описывает количество пловцов на \(i\)-ой дорожке. Сумма этих чисел \(S (0 \le S \le 1500)\).

Выходные данные

Выведите одно целое число - минимальное возможное количество пересечений дорожек, необходимых для достижения хорошего распределения пловцов в бассейне.

Система оценивания

В первой группе тестов \(N\) не превосходят 15, она оценивается в 40 баллов.
Во второй группе тестов \(S\) не превосходит 400, дополнительные ограничения на \(N\) отсутствуют, она оценивается в 25 баллов при условии прохождения всех тестов первой группы.
Во третьей группе тестов дополнительные ограничения отсутствуют, она оценивается в 35 баллов при условии прохождения всех тестов первой и второй групп.

Примеры
Входные данные
3
8 0 2
Выходные данные
5
Входные данные
3
8 5 7
Выходные данные
1
#2920
Перекраска полоски
  

Дана полоска Nx1 клетку, каждая клетка которой раскрашена в один из M цветов. За один ход разрешается перекрасить непрерывную область одного цвета в любой другой цвет.

Требуется определить наименьшее число перекрашиваний, за которое можно получить полоску одного (любого) цвета.

Входные данные

В первой строке находятся два числа N и M – ширина полоски и количество цветов соответственно. 1 ≤ N ≤ 100, 1 ≤ M ≤ 100. Во второй строке находятся N чисел, соответствующих цветам каждой из клеток полоски от 1 до N (сами цвета лежат в диапазоне от 1 до M, каждый цвет встречается хотя бы один раз).

Выходные данные

Выведите одно число – минимальное число перекрашиваний, за которое можно получить полоску одного цвета.

Примеры
Входные данные
5 3
3 2 1 1 3
Выходные данные
2
#2962
Ход конем - 2
  
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes

Дана прямоугольная доска N × M (N строк и M столбцов). В левом верхнем углу находится шахматный конь, которого необходимо переместить в правый нижний угол доски. При этом конь может ходить только так, как показано на рисунке:

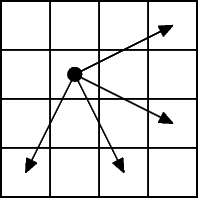
Необходимо определить, сколько существует различных маршрутов, ведущих из левого верхнего в правый нижний угол.

Входные данные

В первой строке входного файла находятся два натуральных числа N и M (1 ≤ N, M ≤ 15).  

Выходные данные

В выходной файл выведите единственное число количество способов добраться конём до правого нижнего угла доски.

Примеры
Входные данные
4 4
Выходные данные
2
Входные данные
7 15
Выходные данные
13309
#2964
Попытка к бегству
  
ограничение по времени на тест
3.0 second;
ограничение по памяти на тест
64 megabytes

Узник пытается бежать из замка, который состоит из N×M квадратных комнат, расположенных в виде прямоугольника NxM. Между любыми двумя соседними комнатами есть дверь, однако некоторые комнаты закрыты и попасть в них нельзя. В начале узник находится в левой верхней комнате и для спасения ему надо попасть в противоположную правую нижнюю комнату. Времени у него немного, всего он может побывать не более, чем в N+M-1 комнате на своем пути, то есть перемещаться он должен только вправо или вниз. Определите количество маршрутов, которые ведут к выходу.

Входные данные

Первая строчка входных данных содержит натуральные числа N и M, не превосходящих 1000. Далее идет план замка в виде N строчек из M чисел в каждой. Одно число соответствует одной комнате: 1 означает, что в комнату можно попасть, 0 – что комната закрыта.

Выходные данные

Программа должна напечатать количество маршрутов, ведущих узника к выходу и проходящих через M+N-1 комнату, или слово Impossible, если таких маршрутов не существует.

Входные данные подобраны таким образом, что искомое число маршрутов не превосходит 2.000.000.000.

Примеры
Входные данные
3 5
1 1 1 1 1
1 0 1 0 1
1 1 1 1 1
Выходные данные
3
Страница: << 18 19 20 21 22 23 24 >> Отображать по:
Выбрано
:
Отменить
|
Добавить в контест