Динамическое программирование на таблицах(46 задач)
Динамическое программирование по подстрокам(21 задач)
Задача о рюкзаке(34 задач)
Напомним, что палиндромом называется строка, которая читается одинаково как слева направо, так и справа налево. Например, палиндромами являются строки «abba» и «madam».
Для произвольной строки s введем операцию деления пополам, обозначаемую half(s). Значение half(s) определяется следующими правилами:
Если s не является палиндромом, то значение half(s) не определено;
Если s имеет длину 1, то значение half(s) также не определено;
Если s является палиндромом четной длины 2m, то half(s) — это строка, состоящая из первых m символов строки s;
Если s является палиндромом нечетной длины 2m + 1, большей 1, то half(s) — это строка, состоящая из первых m + 1 символов строки s.
Например, значения half(inforamatics) и half(i) не определены, half(аbbа) = ab, half(madam) = mad.
Палиндромностью строки s будем называть максимальное число раз, которое можно применить к строке s операцию деления пополам, чтобы результат был определен.
Например, палиндромность строк «informatics» и «i» равна 0, так как к ним нельзя применить операцию деления пополам даже один раз. Палиндромность строк «abba» и «madam» равна 1, а палиндромноств строки «totottotot» равна 3, посколвку операция деления пополам применима к ней три раза:
«totottotot» —> «totot» —> «tot» —> «to».
Задана некоторая строка s. Необходимо изменить в ней минимальное число символов так, чтобы ее палиндромность стала равной k.
Первая строка входного файла содержит число k (\(0 \leq k \leq 20\)). Вторая строка входного файла содержит непустую строку s, состоящую из строчных букв латинского алфавита. Ее длина не превосходит \(10^5\) символов.
В выходной файл выведите минимальное число символов, которое требуется изменить, или —1, если требуемым образом изменить строку невозможно.
2 abaabc
1
1 ababa
1
2 aa
-1
В городе Z в час пик очень оживленное движение. Неправильно выбранный маршрут может на долгое время задержать вас в пути. Вам известно, что схема города представляет собой N горизонтальных и M вертикальных односторонних дорог, образующих прямоугольник N-1 на M-1 километр. На пересечении каждой вертикальной и горизонтальной дороги находится перекресток, на котором можно изменить направление движения. Заметьте, что для изменения направления движения нужно сначала полностью затормозить.
Вы находитесь в точке (1, 1), или другими словами, в левом нижнем углу города. Движение происходит слева направо и снизу вверх. Вам необходимо добраться до точки (N, M) за наименьшее время. Проблема в том, что на каждой дороге свой скоростной режим и максимальное ускорение, которое можно развить, разное для каждой дороги (и равно, соответственно, \(A_i\) км/\(c^2\) для вертикальной дороги с номером i и \(B_j\) км/c2 для горизонтальной дороги с номером j). При этом скорость на дорогах не ограничена. Ускорение и торможение происходит по стандартным физическим законам.
Однако ваше преимущество состоит в том, что вы хорошо знаете город и можете попасть напрямую с перекрестка (i, j) на перекресток (i+1, j+1), в объезд главных дорог (перед этим также нужно полностью затормозить). Время, необходимое для этого, не зависит от номера перекрестка и равно C.
Дороги пронумерованы в порядке, соответствующем направлению движения. Напомним, что движение на всех дорогах одностороннее.
В первой строке входного файла расположены числа \(N\), \(M\) и \(C\) (\(1 \leq N, M \leq 1000\), \(10^{-3} \leq C \leq 10\)). Далее, во второй и третьей строках расположены числа \(A_1\), ..., \(A_N\) и \(B_1\), ..., \(B_M\), соответственно (\(10^{-3} \leq A_i, B_i \leq 10\)).
В первой строке выходного файла выведите искомое время с восемью знаками после запятой. Во второй строке укажите количество перекрестков \(K\), через которые проходит маршрут, включая первый и последний. Далее, в \(K\) строчках выведите координаты соответствующих перекрестков. Выведите координаты только тех перекрестков, где нужно затормозить(учтите, что после каждого переезда по диагонали нужно затормозить).
2 2 4.0 2.0 2.0 2.0 2.0
2.82842712 3 1 1 1 2 2 2
Поле размером \(N\times M\) клеток заполнено целыми числами. Требуется найти на поле клетку, из которой волна, запущенная не более чем на \(K\) итераций, покроет площадь с максимальной суммой расположенных на ней чисел.
Пример распространения волны для поля размером \(5\times 4\). Волна запущена из клетки (3, 3) и была остановлена после трех итераций. Белые клетки – клетки, не покрытые волной, серые и черные – клетки, покрытые волной. Клетки, покрытые волной на последней итерации, отмечены серым цветом.
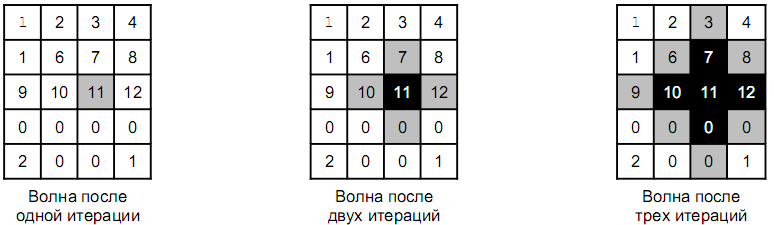
В первой строке входного файла содержатся три целых числа через пробел \(N\), \(M\) и \(K\) (\(1 \leq N, M \leq 100\), \(1 \leq K \leq N + M\)). Следующие \(N\) строк содержат по \(M\) чисел, каждое из которых не превосходит \(10000\) по абсолютной величине.
Выведите четыре числа \(R\), \(C\), \(P\) и \(S\), где \(R\) – номер строки, \(C\) – номер столбца, из которых следует запустить волну, \(P\) – количество итераций распространения волны, \(S\) – максимальная сумма чисел, покрытых волной. Если существует несколько вариантов ответа, то вывести любой, в котором число \(P\) минимально. \(1 \leq P \leq K\).
Решение, верно работающее при \(N, M \leq 15\) будет получать 50 баллов. Эти баллы выставляются при прохождении всех тестов группы. В оставшихся тестах \(N, M \leq 100\), эта группа оценивается при прохождении всех тестов группы.
5 4 3 1 2 3 4 1 6 7 8 9 10 11 12 0 0 0 0 2 0 0 1
3 3 3 66
В сервисной компании по обслуживанию системы продажи театральных билетов работают целых три инженера технической поддержки. Время от времени, в театральных кассах, расположенных в разных частях города, возникают проблемы, и необходимо, чтобы туда приехал один из инженеров.
Кассы занумерованы от \(1\) до \(L\). При поступлении нового вызова, один из инженеров едет к этой кассе из своего текущего положения (или остается там же, если он к тому моменту был в этой кассе). В одной кассе может находиться только один инженер. Вызовы должны обслуживаться в том порядке, в котором они поступают. В каждый момент времени перемещаться может только один инженер. Перемещаться инженеры могут только при вызове и только к той кассе, в которую их вызывают в данный момент. Изначально инженеры находятся в кассах 1, 2 и 3 соответственно. Перемещение инженера из кассы \(p\) в кассу \(q\) стоит \(C(p, q)\) рублей. При этом стоимость проезда из \(p\) в \(q\) и обратно может различаться. Также инженер может совершенно бесплатно оставаться в той же кассе (т.е. \(C(p, p) = 0\)). Цель компании – снизить расходы на обслуживание вызовов. Кроме этого требуется по известной последовательности вызовов определить для каждого из них, каким инженером этот вызов будет обслужен.В первой строке содержаться два числа \(L\) и \(N\) (\(3 \leq L \leq 200\), \(1 \leq N \leq 1000\)) – количество касс и вызовов соответственно. В каждой из следующих \(L\) строк записано по \(L\) целых неотрицательных чисел. Число, стоящее в строке \(p+1\) входного файла и столбце \(q\), задает \(C(p, q)\). Стоимость проезда между двумя кассами – целое неотрицательное число, не превышающее 2000. После этого задано \(N\) чисел – номера касс в той последовательности, в которой происходили вызовы.
Выведите в первой строке минимальную суммарную стоимость переездов. Во второй строке для каждого вызова выведите, каким инженером он будет обслужен.
5 9 0 1 1 1 1 1 0 2 3 2 1 1 0 4 1 2 1 5 0 1 4 2 3 4 0 4 2 4 1 5 4 3 2 1
5 1 2 1 2 2 1 3 1 3
Антон - большой любитель компьютерных игр. Совсем недавно вышла новая игра Heroes of Keyboard and Mouse, и он, конечно же, сразу ее купил и установил на свой компьютер. Эта игра относится к жанру квестов, и поэтому ее прохождение сводится к последовательному выполнению ряда заданий (квестов).
Один из квестов, над которым Антон бьется уже не первый день состоит в том, что требуется открыть замок. Замок состоит из \(n\) шестеренок, стоящих в ряд - \(i\)-ая из шестеренок имеет \(s_i\) зубцов, на каждом из которых написано число от \(0\) до \(s_i - 1\). Первая шестеренка зацеплена только со второй, вторая зацеплена с первой и третьей, третья - со второй и четвертой, ..., \((n-1)\)-ая - с \((n-2)\)-ой и \(n\)-ой, \(n\)-ая только с \((n-1)\)-ой.
На замке имеется \(n\) окошечек и \(n\) ручек - в \(i\)-ое окошко можно видеть число, написанное на одном из зубцов \(i\)-ой шестеренки, а с помощью \(i\)-ой ручки можно поворачивать \(i\)-ую шестеренку. При этом числа на шестеренках расположены таким образом, что если до поворота \(i\)-ой из них по часовой стрелке на одно деление в \(i\)-ом окошке было видно число \(x\), то после поворота будет видно число \((x+1) \bmod s_i\). Аналогично, после поворота против часовой стрелки на одно деление вместо числа \(x\) будет видно число \((x-1+s_i) \bmod s_i\). Разумеется, если шестеренку повернуть по часовой стрелке, то непосредственно зацепленные с ней шестеренки повернутся против часовой стрелки, и наоборот, если шестеренку повернуть против часовой стрелки, то они повернутся по часовой стрелке. Слева на рис.1 показано положение шестеренок до поворота первой из них по часовой стрелке, справа на рис. 1 показано положение шестеренок после указанного поворота. Более толстыми линиями нарисован тот зубец шестеренки, число на котором видно в соответствующее окошко замка.
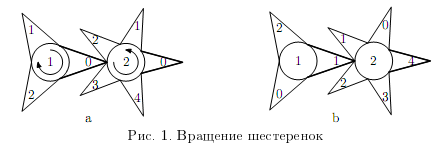
Изначально замок находится в состоянии, в котором в \(i\)-ое окошко видно число \(a_i\). Для того, чтобы его открыть, необходимо перевести его в состояние, в котором в \(i\)-ое окошко видно число \(b_i\).
С помощью \(i\)-ой ручки можно поворачивать \(i\)-ую шестеренку. Разумеется, если повернуть \(i\)-ую шестеренку, то придут в движение и все шестеренки, с которыми она соединена - напрямую или через другие шестеренки. Поворот любой шестеренки на одно деление занимает одну секунду. Кроме этого, если \(i\)-ая шестеренка находится в таком состоянии, что в \(i\)-ое окошко видно число \(b_i\) (то есть, она находится в положении, соответствующем требуемому состоянию замка), то ее можно вдавить, нажав на ее ручку. В результате этого \(i\)-ая шестеренка перестает быть соединенной с \((i-1)\)-ой и \((i+1)\)-ой (если, конечно, они существуют). Вдавленная шестеренка остается в таком состоянии навсегда. На то, чтобы нажать на ручку и вдавить шестеренку требуется \(k\) секунд. На рис. 2 слева показано положение шестеренок до вдавливания второй из них, а справа - после вдавливания и после поворота первой по часовой стрелке, а третьей - против. Отметим, что после вдавливания второй шестеренки первая и третья вращаются независимо друг от друга.
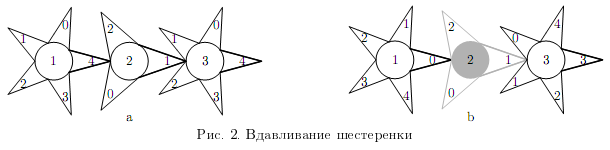
Для того, чтобы выполнить квест, Антону необходимо открыть замок как можно быстрее. Напишите программу, которая по описанию замка, его начального состояния и требуемого состояния, вычислит минимальное время, за которое Антон может открыть замок.
Первая строка входного файла содержит два целых числа: \(n\) и \(k\) (\(1 \le n \le 25\), \(1 \le k \le 100\)). Вторая строка входного файла содержит \(n\) чисел: \(s_1\), \(s_2\), ..., \(s_n\) - размеры шестеренок. Все \(s_i\) - целые числа от 3 до 10. Третья строка входного файла содержит \(n\) целых чисел \(a_1\), \(a_2\), ..., \(a_n\) - начальные положения шестеренок (для всех \(a_i\) выполняются неравенства \(0 \le a_i < s_i\)). Четвертая строка входного файла содержит \(n\) целых чисел \(b_1\), \(b_2\), ..., \(b_n\) - требуемые положения шестеренок (для всех \(b_i\) выполняются неравенства \(0 \le b_i < s_i\)).
В выходной файл выведите минимальное количество времени, которое необходимо для того, чтобы открыть замок.
2 2 3 5 0 0 1 1
4
3 2 3 3 3 0 0 0 1 1 1
5