Власти Флатландии решили построить новый мост через реку Нижний Флат, протекающую с юга на север через территорию страны. В связи с финансовым кризисом средства строителей существенно ограничены, поэтому решено было построить мост минимальной возможной длины. 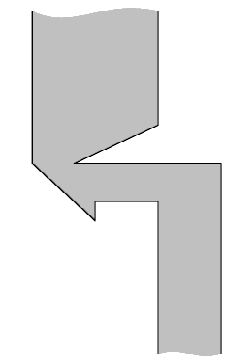
Введем координатную систему таким образом, чтобы ось OY была направлена с юга на север, а ось OX с запада на восток. Берега реки представляют собой ломаные, бесконечные в обе стороны. Левый берег начинается лучом, направленным на юг из точки (x1,1,y1,1), продолжается отрезками (x1,1,y1,1) − (x1,2,y1,2), (x1,2,y1,2)− (x1,3,y1,3), ..., (x1,m−1,y1,m−1) − (x1,m,y1,m) и заканчивается лучом, направленным на север из точки (x1,m,y,m).
Аналогично, правый берег реки начинается лучом, направленным на юг из точки (x2,1,y2,1), продолжается отрезками (x2,1,y2,1) − (x2,2,y2,2), (x2,2,y2,2) − (x2,3,y2,3), ..., (x2,n−1,y2,n−1) − (x2,n,y2,n) и заканчивается лучом, направленным на север из точки (x2,n,y2).
Помогите руководству Флатландии выяснить, мост какой минимальной длины можно построить.
Первая строка входного файла содержит целое число m (2 ≤ m ≤ 100). Следующие m строк содержат по два целых числа координаты вершин ломаной левого берега: x1,1, y1,1, x1,2,y1,2, ...,x1,m, y1,m.
Следующая строка входного файла содержит целое число n (2 ≤ n ≤ 100). Следующие n строк содержат по два целых числа координаты вершин ломаной правого берега: x2,1, y2,1, x2,2, y2,2, ..., x2,n, y2,n.
Известно, что x1,1 < x2,1, каждая из ломаных не имеет самопересечений и самокасаний, ломаные не имеют общих точек. Все отрезки каждой из ломаных имеют положительную длину. Все координаты не превосходят 104 по абсолютной величине
Выведите в выходной файл одно вещественное число: минимальную возможную длину моста. Ваш ответ будет проверяться с точностью 10−5.
Оптимальное положение моста показано на следующем рисунке:
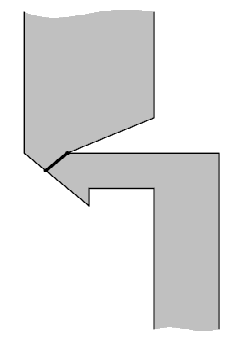
4 6 1 3 1 3 0 0 3 3 9 3 2 3 6 5
1.4142135623730951
«Кто ходит в гости по утрам, тот поступает мудро…»
Пятачок и Винни-Пух каждое утро ходят пить чай в гости к Кролику. Естественно, самым коротким путем.
К сожалению, однажды Винни-Пуху пришла в голову идея вырыть ловушку для Слонопотама. Самое обидное, что они с Пятачком ее даже вырыли. Поэтому теперь каждое утро, идя в гости к Кролику, они боятся в нее провалиться.
Напишите программу, которая посчитает длину самого короткого безопасного пути от домика Винни-Пуха до домика Кролика.
Ловушка для Слонопотама представляет собой яму абсолютно круглой формы. Путь является безопасным, если он не проходит по ловушке (но может проходить по ее границе).
Во входном файле записаны сначала координаты домика Винни-Пуха XВ YВ, затем — координаты домика Кролика XК YК, а затем — координаты центра и радиус ловушки XЛ YЛ RЛ. Все координаты — целые числа из диапазона от –32000 до 32000. Радиус ловушки — натуральное число, не превышающее 32000.
Домики Винни-Пуха и Кролика не могут находиться внутри ловушки, но могут находиться на ее границе.
Выведите в выходной файл одно число — длину самого короткого безопасного пути от домика Винни-Пуха до домика Кролика с тремя знаками после точки.
0 0 10 0 5 5 1
10.000
3 4 4 4 0 0 5
1.000
Движением плоскости называют такое преобразование плоскости, которое сохраняет попарные расстояния между точками, то есть если A1 и B1 – образы некоторых точек A и B при движении, то |A1B1| = |AB|.
Одной из разновидностей движения плоскости является скользящая симметрия. Скользящей симметрией называют композицию симметрии относительно некоторой прямой l и переноса на вектор, параллельный l (этот вектор может быть нулевым). На рисунке показан пример применения скользящей симметрии к отрезку.
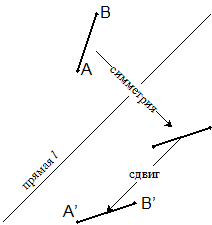
Известно, что любой отрезок можно перевести в любой другой отрезок такой же длины с помощью скользящей симметрии.
Требуется по координатам двух различных точек A и B и двух точек A1 и B1, находящихся на таком же расстоянии друг от друга, как и точки A и B, найти скользящую симметрию, переводящую точку A в точку A1, а точку B в точку B1.
В первой строке входного файла находятся четыре целых числа – координаты двух различных точек A и В. Во второй строке также находятся четыре целых числа – координаты двух различных точек A1 и В1. Гарантируется, что |A1B1| = |AB|. Все числа во входном файле по модулю не превышают 1000. Числа в строках разделены пробелом.
Выведите в выходной файл описание искомой скользящей симметрии, которое представляется в следующем виде.
В первой строке должны выводиться координаты двух различных точек, лежащих на прямой l, относительно которой выполняется симметрия, а во второй – координаты вектора, параллельного этой прямой, на который осуществляется перенос. Вещественные числа должны быть представлены не менее чем с 6 знаками после десятичной точки.
1 1 3 2 -1 1 -3 2
0.000000 0.000000 0.000000 1.000000 0.000000 0.000000
1 1 3 1 3 -1 5 -1
0.000000 0.000000 1.000000 0.000000 2.000000 0.000000
На координатной плоскости расположены равнобедренный прямоугольный треугольник ABC с длиной катета d и точка X. Катеты треугольника лежат на осях координат, а вершины расположены в точках: A (0,0), B (d,0), C (0,d).
Напишите программу, которая определяет взаимное расположение точки X и треугольника. Если точка X расположена внутри или на сторонах треугольника, выведите 0. Если же точка находится вне треугольника, выведите номер ближайшей к ней вершины.
Сначала вводится натуральное число d(не превосходящее 1000), а затем координаты точки X – два целых числа из диапазона от –1000 до 1000.
Если точка лежит внутри, на стороне треугольника или совпадает с одной из вершин, то выведите число 0. Если точка лежит вне треугольника, то выведите номер вершины треугольника, к которой она расположена ближе всего (1 – к вершине A, 2 – к B, 3 – к C). Если точка расположена на одинаковом расстоянии от двух вершин, выведите ту вершину, номер которой меньше.
1. Точка лежит внутри треугольника.
2. Точка лежит вне треугольника и ближе всего к ней вершина A
3. Точка лежит на равном расстоянии от вершин B и C,в этом случае нужно вывести ту вершину, у которой номер меньше, т.е. выведено должно быть число 2
4. Точка лежит на стороне треугольника.
5 1 1
0
3 -1 -1
1
4 4 4
2
4 2 2
0
На новой станции метро, которую планируют открыть в конце этого года, будет N эскалаторов (эскалаторы пронумерованы подряд числами от 1 до N). Эскалаторы имеют длину L и расположены на расстоянии H друг от друга. Шириной эскалатором пренебрежем. Между каждыми двумя соседними эскалаторами (точно посередине) будет установлен ряд ламп. В ряду будет K ламп. Лампы устанавливаются по следующему принципу: всю длину эскалатора L разбивают на K равных отрезков и в середине каждого отрезка устанавливают по лампе (см. рисунок). Всего будет установлено (N–1)*K ламп.
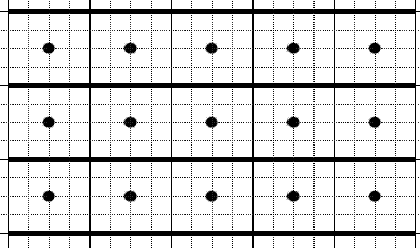
На приведенном рисунке N=4 (эскалаторы показаны жирными <горизонтальными линиями), L=20, H=4, K=5.
Васе удалось проникнуть на эту станцию еще до ее открытия, и даже прокатиться на эскалаторе. Он выбрал эскалатор номер J. Посчитайте, в скольких точках эскалатора (включая его начало и конец) Вася будет видеть не все лампы (так как их будут загораживать другие лампы).
Во входном файле записаны числа N, L, H, K, J. Все числа — натуральные. 2≤N≤35, 1≤L≤1000, 1≤H≤1000, 1≤K≤35, 1≤J≤N.
В выходной файл выведите одно число — ответ задачи.
2 20 4 5 1
0
4 20 4 5 2
11