--->
144 задач
<---
Источники
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes
Петр Васильевич в ярости! Ведь сосед Василий Петрович выгуливал козла в его огороде! Как не предусмотрителен был Василий Петрович ведь у Петра Васильевича целых 2 козла и оба они в ответ будут поедать и вытаптывать соседский огород. Огород Василия Петровича большой и неогороженный, в некоторых его местах растут деревья. Козлам потребуется много времени, чтобы выполнить свою миссию. Поэтому Петр Васильевич решил привязать каждого козла к какому-нибудь дереву, и пусть себе гуляют. Но привязать каждого надо так, чтобы он не доставал до всех деревьев кроме того, к которому он привязан, иначе он запутается в веревке. Кроме того, надо чтобы они не доставали друг до друга, иначе они будут вытаптывать одну и ту же территорию. Чтобы нанести максимальный вред своему соседу, Петр Васильевич хочет, чтобы суммарная площадь, доступная козлам была максимальна. Но нельзя привязывать козла на расстоянии меньше 1 метра от дерева и дальше, чем на 50 метров.
Входные данные
В первой строке записано целое число \(N\) \((2 \le N \le 1000)\) — количество деревьев в огороде. В следующих \(N\) строках записаны координаты деревьев. Начало координат совмещено с центром огорода, координаты даны в метрах с точностью до сантиметра. Координаты деревьев по модулю не превосходят 100 метров. Можно считать, что нельзя привязать козла так, чтобы он смог выйти за пределы огорода. Размерами самих козлов можно пренебречь. Гарантируется, что козлов всегда можно привязать надлежащим образом.
Выходные данные
Выведите максимальную площадь, которую смогут вытоптать козлы Петра Васильевича, с точностью не менее 6 знаков после запятой.
Примеры
Входные данные
8 1 1 -2 0 5 3 -2 3 8 3.10 -2 -1 -2 2 8 4.10
Выходные данные
36.8060473804
#3870
Источники:
[
Личные олимпиады,
Всероссийская олимпиада школьников,
Региональный этап,
2012,
2 день,
Задача C
]
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
256 megabytes
На планете Плюк открылся новый космический кегельбан. Поле для кегельбана представляет собой бесконечную плоскость, на которой расставлены кегли.
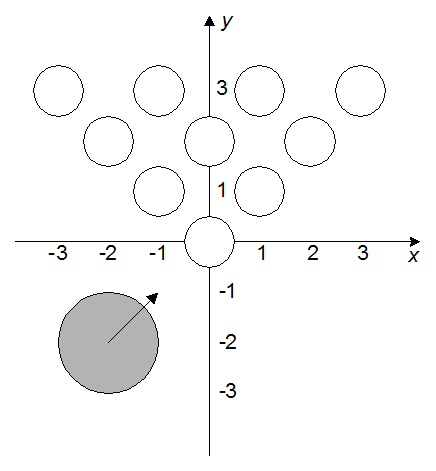
Каждая кегля представляет собой высокий цилиндр с основанием в виде круга радиусом r метров. Все кегли одинаковые. Кегли расставлены по следующим правилам. Кегли образуют n рядов, в первом ряду стоит одна кегля, во втором — две, и так далее. В последнем n-м ряду стоит n кеглей. Введем на плоскости систему координат таким образом, чтобы единица измерения была равна одному километру. Центр единственной кегли в первом ряду находится в точке (0, 0). Центры кеглей во втором ряду находятся в точках (–1, 1) и (1, 1). Таким образом, центры кеглей в i-м ряду находятся в точках с координатами (–(i – 1), i – 1), (–( i – 3), i – 1), …, (i – 1, i – 1).
Игра происходит следующим образом. Используется шар с радиусом q метров. Игрок выбирает начальное положение центра шара (xc, yc) и вектор направления движения шара (vx, vy). После этого шар помещается в начальную точку и двигается, не останавливаясь, в направлении вектора (vx, vy). Считается, что шар сбил кеглю, если в процессе движения шара имеет место ситуация, когда у шара и кегли есть общая точка. Сбитые кегли не меняют направления движения шара и не сбивают соседние кегли при падении.
На рисунке приведен пример расположения кеглей для r = 500, n = 4 и шара для q = 1000, xc = –2, yc = –2, vx = 1, vy = 1.
Требуется написать программу, которая по заданным радиусу кегли r, количеству рядов кеглей n, радиусу шара q, его начальному положению ( xc, yc) и вектору направления движения (vx, vy) определяет количество кеглей, сбитых шаром.
Входные данные
Первая строка входного файла содержит два целых числа: r и n, разделенных ровно одним пробелом (1 ≤ r ≤ 700, 1 ≤ n ≤ 200 000).
Вторая строка входного файла содержит целое число q (1 ≤ q ≤ 109).
Третья строка входного файла содержит два целых числа xc и yc, разделенных ровно одним пробелом (–106≤ xc ≤ 106, –10 6≤ yc, 1000 ×yc < –(r + q) ).
Четвертая строка входного файла содержит два целых числа vx и vy, разделенных ровно одним пробелом (–106≤ vx ≤ 106, 0 < vy ≤ 106).
Выходные данные
Выходной файл должен содержать одно целое число — количество сбитых кеглей.
Примечание
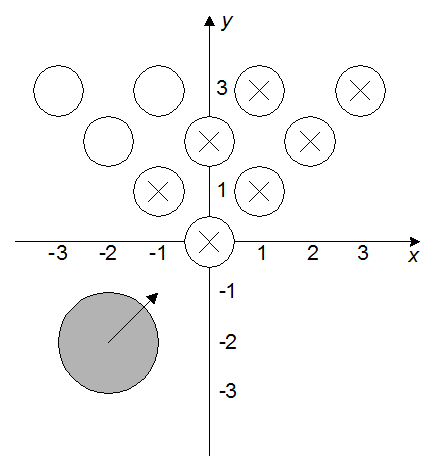
Рисунок ниже показывает, какие кегли будут сбиты (такие кегли обозначены «х»).
Система оценки
Потестовая.
Примеры
Входные данные
500 4 1000 -2 -2 1 1
Выходные данные
7
#3881
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
256 megabytes
Компания, производящая оборудование для сотовой связи, обратилась к вам с просьбой написать программу, оценивающую качество организации сети. Одним из важных параметров является то, пересекаются ли зоны покрытия передатчиков, работающих на одинаковых частотах. Для простоты будем считать, что область покрытия каждого передатчика представляет собой многоугольник на плоскости (не обязательно выпуклый). Две области покрытия будем считать пересекающимися, если у них есть хотя бы одна общая точка (возможно, лежащая на границе одной или даже обеих областей). Ваша программа должна принимать на вход набор пар многоугольников, описывающих зоны покрытия передатчиков, и выводить про каждую пару информацию о том, пересекаются ли эти зоны.
Входные данные
На первой строке входного файла находится число \(K\) — количество тестов во входном файле. Далее идёт описание \(K\) тестов. Каждый тест задаётся описанием двух многоугольников, которые надо проверить на пересечение. Каждый многоугольник задаётся в следующем формате: сначала указывается одно число \(N_i\) — число вершин этого многоугольника, после чего идут \(N_i\) строк, каждая из которых содержит два разделённых пробелом числа \(x_{ij}\) и \(y_{ij}\) — координаты \(j\)-й вершины этого многоугольника. Вершины перечислены в порядке обхода многоугольника.
Число пар многоугольников в одном тесте \(1 \leq K \leq 10\), число вершин каждого многоугольника \(3 \leq N_i \leq 100\), координаты вершин — целые числа, \(|x_{ij}|, |y_{ij}| \leq 10\,000\).
Выходные данные
Для каждой пары многоугольников выведите в выходной файл на отдельной строке одно слово: “YES”, если многоугольники пересекаются, и “NO”, если нет.
Примеры
Входные данные
2 3 0 0 -1 0 0 -1 3 1 1 2 1 1 2 4 0 0 2 0 2 2 0 2 4 1 1 3 1 3 3 1 3
Выходные данные
NO YES
#3894
Темы:
[Элементарная геометрия]
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
256 megabytes
Фирма, в которой всё ещё работает ваш друг, собирается расширяться на новые маршруты, и потому приобрела
новую площадку для ночного отстоя автобусов. Площадка раньше относилась к военной части, поэтому
она имеет необычную форму — форму треугольника, огороженного забором.
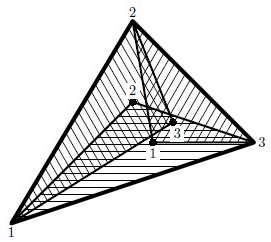
Для того, чтобы освещать площадку ночью, на ней надо установить несколько прожекторов. К счастью, у фирмы как раз в наличие есть три регулируемых прожектора, а на территории площадки обнаружились три высоких столба. Было решено на каждый столб повесить по прожектору и отрегулировать их так, чтобы каждый прожектор освещал ровно одну из трёх сторон забора: один прожектор должен освещать одну сторону забора, другой — другую, третий — третью. Никакой прожектор не должен освещать ни миллиметра “чужой” стены.
Конечно, прожекторы должны освещать не только забор, но вообще всю территорию площадки, поэтому возникла проблема: надо определить, какой прожектор на какую сторону забора направить. Зная ваши высокие навыки в решении подобных задач, фирма обратилась к вам за помощью. Напишите программу, которая будет решать эту задачу.
Естественно, каждый прожектор освещает не только стену, но и всю соответствующую часть двора — треугольник с вершиной в месте, где находится столб, на котором висит прожектор, и основанием, совпадающим с соответствующей стороной забора. Будем считать, что стороны этого треугольника тоже освещены прожектором. Тенью от столбов пренебрегайте.
Входные данные
Первая строка входного файла содержит одно число \(T\) — количество тестовых примеров, которые идут дальше (\(1\leq T\leq 1000\)).
Далее следуют описания \(T\) примеров. В каждом сначала идут шесть чисел \(x_1\), \(y_1\), \(x_2\), \(y_2\), \(x_3\), \(y_3\) — координаты вершин площадки, после чего идут шесть чисел \(X_1\), \(Y_1\), \(X_2\), \(Y_2\), \(X_3\), \(Y_3\) — координаты столбов. Гарантируется, что все столбы находятся строго внутри площадки. Гарантируется, что площадь площадки строго больше нуля. Гарантируется, что никакие два столба не совпадают. Все координаты во входном файле целые и не превосходят по модулю \(800\).
Выходные данные
Выведите в выходной файл \(T\) строк по три числа в каждой: для каждого примера выведите номер стороны забора, на которую должен светить прожектор, находящийся на первом столбе, потом номер стороны, на которую должен светить прожектор со второго столба, и наконец номер стороны, на которую должен светить прожектор с третьего столба.
Первая сторона — та, которая соединяет вершины \((x_1, y_1)\) и \((x_2, y_2)\), вторая — \((x_2, y_2)\) и \((x_3, y_3)\), третья — \((x_3, y_3)\) и \((x_1, y_1)\).
Если решения не существует, выведите в соответствующую строку выходного файла три минус единицы:
“-1 -1 -1”.
Примечание
Первый пример соответствует рисунку.
Среди тестов будут такие, в которых \(T\leq 10\); суммарная стоимость таких тестов будет 70 баллов.
Примеры
Входные данные
2 0 0 6 10 12 4 7 4 6 6 8 5 -10 -10 0 10 10 -10 0 1 0 -1 1 1
Выходные данные
2 3 1 3 2 1
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
256 megabytes
Реализуйте class LinEquation
Выбрано
:
|