В одном очень большом городе устраивают необычные скачки. От обычных скачек они отличаются тем, что проходят не на ипподроме, а на специально заготовленной трассе. Она представляет из себя бесконечную прямую на плоскости.
Трасса очень длинная, поэтому соревнования могут затягиваться не на один день и проходить не только днем, но и ночью. Организаторы глубоко задумались о том, как они будут освещать трассу, ведь освещать бесконечно длинную трассу не так уж и просто. Для этого они закупили N прожекторов, которые будут установлены в некоторых точках города. Известно что прожекторы освещают землю, образуя круги.
Так получилось, что компания, которая устанавливала оборудование, перепутала места установки, поэтому некоторые прожекторы могут вообще не освещать трассу. Теперь соревнование может потерпеть неудачу, организаторы очень обеспокоены тем, что зрители не увидят самые интересные моменты соревнований из-за ошибки мастеров. Помогите организаторам выяснить, какова длина освещенной части трассы.
Первая строка входного файла содержит четыре числа x 1 , y 1 , x 2 , y 2 — координаты двух точек на прямой. Во второй — строке число N ( 1 ≤ N ≤ 100000 ) — количество прожекторов. В каждой их следующих N строк заданы 3 числа x , y и R , координаты и радиус кругов, образованных прожекторами.
Все координаты и радиусы — целые числа, не превышающие по модулю 10 5 .
В выходной файл выведите ответ на задачу, с точностью до 10 - 4 .
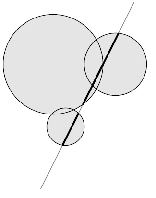
0 0 1 1 1 5 5 1
2.000000000000001
1 1 2 3 3 5 5 5 -5 5 8 -3 -5 3
18.446020156281286
Завтра состоится футбольный матч между двумя знаменитыми командами: Газмясом и Нефтьрыбом. Матч будет проходить на поле длины L и ширины W . Матч будет судить профессиональный футбольный судья в четвертом поколении Вениамин Хлебников.
Быть судьей — ответственное и не всегда безопасное занятие. Поэтому Вениамин решил проработать некоторые игровые эпизоды, которые возникнут в завтрашней игре.
Рассмотрим ситуацию, когда игрок A делает пас игроку B — то есть, передает ему мяч по отрезку, соединяющему точки, в которых находятся игроки. С одной стороны, судья должен хорошо видеть то, что происходит во время паса; с другой стороны, согласно требованиям безопасности, судья не может находиться слишком близко к мячу. Поэтому во время паса судья должен находиться на расстоянии, не меньшем, чем r , и не большем, чем R , от возможного положения мяча. При этом считается, что все то время, в течение которого движется мяч, судья стоит на одном месте. Разумеется, судья должен все время матча находиться на поле.
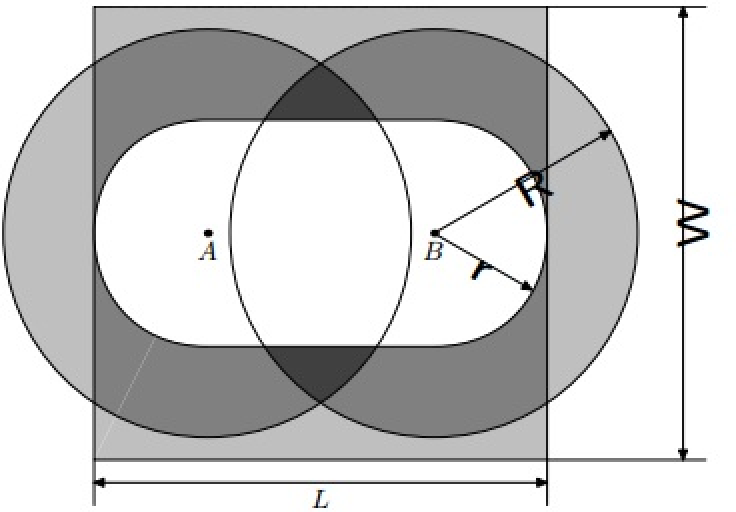
Так как эти условия достаточно сложны, то даже опытному судье иногда бывает трудно определить, где он должен находиться в момент паса. По этой причине Вениамин хочет перед матчем потренироваться находить те области, где он может находиться, при различных начальных условиях. Для того чтобы сравнить свой ответ с правильным, ему необходима программа, которая по заданным размерам поля, координатам игроков и числам r и R находит площадь тех областей поля, в которых может находиться судья. Помогите ему!
В первой строке входного файла даны два целых положительных числа L и W ( 1 ≤ L , W ≤ 100 ) — длина и ширина поля.
Во второй строке даны целые числа X A , Y A , X B , Y B — координаты игроков A и B соответственно. Так как игроки находятся на поле, то 0 ≤ X A , X B ≤ L , 0 ≤ Y A , Y B ≤ W .
В третьей строке даны целые числа
r
и
R
(
0 <
r
<
R
< 100
). Известно, что
R
≤
D
, где
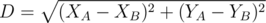 — расстояние между игроками
A
и
B
.
— расстояние между игроками
A
и
B
.
В выходной файл выведите ответ на задачу. Ответ принимается, если он отличается от корректного не более, чем на 10 - 6 .
20 20 5 10 15 10 5 9
13.956675119742911
На протяжении многих лет Вася работает программистом в одной очень большой и очень известной компании. Эта компания обеспечивает своих сотрудников всем необходимым для приятной и плодотворной работы: бесплатными обедами, транспортом от дома до места работы и многим, многим другим. И вот в один прекрасный солнечный день Вася понял, что ему очень наскучил вид из окна его офиса, и ему нужно, чтобы за окном было что-то новое и прекрасное. А что может быть лучше чудесного горного пейзажа? Придя к этой мысли, Вася попросил своего менеджера подобрать себе новый офис с красивым видом на горы.
В той местности, где располагается офис Васи, каждая гора принадлежит некоторой горной цепи. Так как Васе хочется, чтобы вид из окна его офиса был идеальным, то он попросил подобрать себе такой офис, чтобы никакие две горные цепи, видимые из окна, не пересекались. Менеджер Васи нашел прекрасный новый офис, из которого видно N горных цепей, но он никак не может определить, понравится ли Васе вид из окна этого офиса. Помогите ему!
Более формально, вид из окна офиса представляет собой набор горных цепей, пронумерованных от \(1\) до \(N\), где горная цепь с номером i представляет собой ломаную на плоскости из \(l_i\) звеньев с вершинами в точках (\(x_i\),\(j\) , \(y_i\),\(j\) ), причем для любых \(i\), \(j\) выполнено \(x_{i,j} < x_{i,j+1}\).
Кроме этого, окно в офисе имеет фиксированную ширину, поэтому все горные цепи начинаются и заканчиваются на одной вертикали, то есть существуют такие числа \(A\) и \(B\), что для любого номера \(i\) горной цепи выполнено \(x_{i,0} = A, x_{i,l_i} = B\).
Отметим, что из определения горной цепи следует, что для любого значения абсциссы \(A \le x \le B\) на ломаной с номером \(i\) существует единственная точка (\(x\), \(y_i\)(\(x\))) с этим значением абсциссы, принадлежащая этой ломаной. Будем говорить, что горная цепь \(i\) находится строго выше горной цепи \(j\) в точке \(x\), если выполнено строгое неравенство \(y_i(x) > y_j (x)\).
Естественно считать, что цепь под номером \(i\) пересекается с цепью под номером \(j\), если существуют такие два значения абсциссы \(x_1\), \(x_2\), что цепь \(i\) находится строго выше цепи \(j\) в точке \(x_1\), но при этом цепь \(j\) находится строго выше цепи \(i\) в точке \(x_2\), то есть выполнены неравенства \(y_i\)(\(x_1\)) > \(y_j\) (\(x_1\)) и \(y_j\) (\(x_2\)) > \(y_i\)(\(x_2\)). Обратите внимание на поясняющие рисунки, расположенные в примечании к задаче.
Вам необходимо определить, подойдет ли подобранный офис Васе, и, если нет, то найти любую пару пересекающихся горных цепей.
В первой строке входных данных через пробел идут два целых числа: \(A\) и \(B\) (\(−10^9 \le A < B \le 10^9\) ).
Во второй строке входных данных находится единственное число \(N\) — количество горных цепей, видимых из окна подобранного менеджером Васи офиса (\(1 \le N \le 100 000\)).
Далее следуют описания N горных цепей. В первой строке i-го описания содержится число \(l_i \ge 1\) — количество звеньев ломаной, из которых состоит соответствующая горная цепь. В следующих \(l_i\) + 1 строках описания содержатся два целых числа — координаты (\(x_{i, j} , y_{i,j}\) ) вершин ломаной (\(0 \le j \le l_i\)). Суммарное число звеньев всех ломаных не превосходит 200 000.
Гарантируется, что для каждой горной цепи вершины соответствующей ей ломаной идут во входных данных в порядке возрастания абсциссы, причем для любого \(i\) выполнено \(x_{i,0} = A, x_{i,l_i} = B\).
Если же офис подходит Васе, то есть никакие две горные цепи из входных данных не пересекаются, в единственной строке выходных данных выведите слово «Yes» (без кавычек).
Иначе выведите в первой строке слово «No» (без кавычек), а на следующей строке выведите два числа — номера двух пересекающихся горных цепей. Горные цепи нумеруются согласно их появлению во входных данных, начиная с 1.
В первом примере хотя ломаные и касаются друг друга в точке (−3, 2), но, согласно данному выше определению, они не пересекаются.
Во втором примере в точке \(x_1\) = 1 одна ломаная выше другой, а в точке \(x_2\) = 3 — наоборот, то есть горные цепи пересекаются.
Тесты к этой задаче состоят из пяти групп. Баллы за каждую группу ставятся только при прохождении всех тестов группы и всех тестов предыдущих групп. Offline-проверка означает, что результаты тестирования вашего решения на данной группе станут доступны только после окончания соревнования.
-3 3 2 1 -3 2 3 1 2 -3 2 0 4 3 2
Yes
0 4 2 3 0 3 1 3 3 1 4 1 1 0 2 4 2
No 1 2
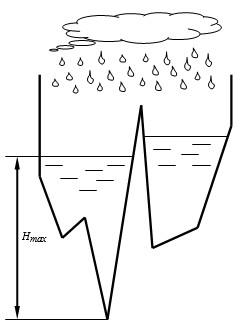
В НИИ метеорологии решили изучить процесс образования водоемов на различных рельефах местности во время дождя. Ввиду сложности реальной задачи была создана двумерная модель, в которой местность имеет только два измерения — высоту и длину. В этой модели рельеф местности можно представить как N-звенную ломаную c вершинами \((x_0, y_0), ..., (x_N, y_N)\), где \(x_0 < x_1 < ... < x_N\) и \(y_i \neq y_j\), для любых \(i \neq j\). Слева в точке \(x_0\) и справа в точке \(x_N\) рельеф ограничен вертикальными горами огромной высоты.
Если бы рельеф был горизонтальным, то после дождя вся местность покрылась бы слоем воды глубины H. Но поскольку рельеф — это ломаная, то вода стекает и скапливается в углублениях, образуя водоемы.
Требуется найти максимальную глубину в образовавшихся после дождя водоемах.
В первой строке расположены натуральное число \(N (1 \le N \le 100)\) и \(H\) — действительное число, заданное с тремя цифрами после десятичной точки \((0 \le H \le 10^9)\). В последующих \(N + 1\) строках — по два целых числа \(x_i, y_i: -10000 \le x_i, y_i \le 10000 (0 \le i \le N)\).
Числа в строках разделены пробелами.
Ответ должен содержать единственное число — искомую глубину с точностью до 4-х знаков после десятичной точки.
7 7.000 -5 10 -3 4 -1 6 1 -4 4 17 5 3 9 5 12 15
15.8446
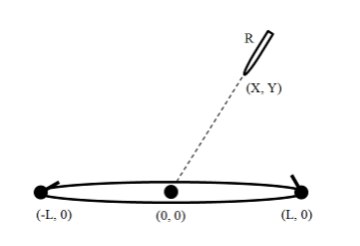
На координатной плоскости вдоль оси OX, симметрично относительно начала координат, мирно расположился крейсер «Адмирал Василий». Крейсер расположен так, что его центр находится в точке (0, 0) , нос (передняя часть) — в точке (− L , 0) , а корма (задняя часть) — в точке ( L , 0) . Отнюдь не мирные цели визита «Адмирала Василия» на координатную плоскость выдают лишь две его установки ПВО, расположенные на носу и корме крейсера то есть в точках (− L , 0) и ( L , 0) .
Хранители координатной плоскости не рады незваным гостям. С целью предотвращения потенциальной угрозы была выпущена ракета, направленная ровно в начало координат — центр крейсера. Ракета имеет длину
R
, на момент запуска нос ракеты находился в точке
(
X
,
Y
)
. Ракета расположена вдоль прямой, соединяющей нос ракеты и начало координат. Скорость полета ракеты —
V
(см.рисунок).
Как только ракета была запущена, её обнаружил крейсер и обе установки ПВО открыли огонь по ракете.
Установки ПВО работают следующим образом:
•они мгновенно поворачиваются, наводятся на нос ракеты и производят выстрел в этом направлении;
•скорость снаряда установки ПВО равна W ;
•установки ПВО продолжают стрелять до тех пор, пока ракета не будет уничтожена или пока крейсер не будет потоплен;
•первый выстрел установки ПВО производят в момент запуска ракеты, последующие выстрелы производятся с интервалом времени T , то есть между двумя выстрелами ракета пролетает расстояние V · T .
Если снаряд установки ПВО попадет в какую-то часть ракеты, то ракета будет уничтожена. При этом, если ракета достигнет носом центра крейсера, то , в свою очередь, крейсер будет потоплен. Какой минимальной скоростью W должны обладать снаряды установок ПВО, чтобы сбить ракету до того, как она уничтожит крейсер? Размерами снарядов установок ПВО, шириной крейсера и шириной ракеты можно пренебречь. Установки ПВО поворачиваются мгновенно. Первый выстрел они производят в момент запуска ракеты, а затем производят выстрелы с интервалом ровно T .
В первой строке входного файла содержится единственное число L — расстояние от центра крейсера до его концов ( 1 ≤ L ≤ 1000 ). Во второй строке находятся координаты носа ракеты на момент запуска — X , Y ( −1000 ≤ X ≤ 1000 , 1 ≤ Y ≤ 1000 ). В третьей строке описаны характеристики ракеты—ее длина R и скорость полета V ( 1 ≤ R , V ≤ 1000 ). В четвертой строке записано единственное число T — интервал времени между выстрелами установок ПВО ( 1 ≤ T ≤ 1000 ). Все числа во входном файле целые.
Выведите единственное число с абсолютной или относительной погрешностью не более 10 −6 — минимальную скорость снарядов установок ПВО, при которой ракету удастся сбить до того, как она потопит крейсер.
В первом примере ракета потопит крейсер через время 2. Поскольку интервал между выстрелами ПВО равен 3, то ракету нужно сбить первым выстрелом.
Во втором примере интервал между выстрелами равен 1. Значит, ракету можно сбить вторым выстрелом, для этого достаточно меньшей скорости снаряда по сравнению с первым примером.
2 0 6 2 3 3
9.486833
2 0 6 2 3 1
5.408327