--->
144 задач
<---
Источники
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes
Выведите все исходные точки в порядке возрастания их расстояний от начала координат.
Создайте структуру Point и сохраните исходные данные в массиве структур Point.
Входные данные
Программа получает на вход набор точек на плоскости. Сначала задано количество точек n, затем идет последовательность из n строк, каждая из которых содержит два числа: координаты точки. Величина n не превосходит 100, все исходные координаты – целые числа, не превосходящие 103.
Выходные данные
Необходимо вывести все исходные точки в порядке возрастания их расстояний от начала координат. Программа выводит только координаты точек, их количество выводить не надо.
Примеры
Входные данные
2 1 2 2 3
Выходные данные
1 2 2 3
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes
Среди исходных точек найдите три, образующие треугольник с максимальным периметром. Выведите данный периметр.
Входные данные
Программа получает на вход набор точек на плоскости. Сначала задано количество точек n (2<n<101), затем идет последовательность из n строк, каждая из которых содержит два числа: координаты точки. Все исходные координаты – целые числа, не превосходящие 103.
Выходные данные
Необходимо вывести найденный периметр с точностью в 15 значащих цифр.
Примеры
Входные данные
4 0 0 0 1 1 0 1 1
Выходные данные
3.41421356237309
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes
Среди исходных точек найдите три, образующие треугольник максимальной площади. Выведите данную площадь.
Создайте структуру Point и сохраните исходные данные в массиве структур Point.
Входные данные
Программа получает на вход набор точек на плоскости. Сначала задано количество точек n (2<n<101), затем идет последовательность из n строк, каждая из которых содержит два числа: координаты точки. Все исходные координаты – целые числа, не превосходящие 10 3.
Выходные данные
Необходимо вывести найденную площадь с точностью в 15 значащих цифр.
Примеры
Входные данные
4 0 0 0 1 1 0 1 1
Выходные данные
0.5
#407
Темы:
[Элементарная геометрия]
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
256 megabytes
Картины художников-абстракционистов весьма необычны. На них часто изображены абсолютно непонятные предметы. Один известный художник-абстракционист решил добавить своим картинам оригинальности следующим способом. Вместо прямоугольных рамок, в которые обычно вставляются картины, он решил на ближайшей выставке использовать треугольные.
Однако все оказалось совсем не так просто. Художник изготовил рамку, поместил в нее картину и понял, что что-то не так. Рамка получилась слишком широкой, и картина выглядела совсем не так ярко, как он ожидал.
Немного поразмыслив, художник понял, что то, насколько рамка «подходит» для картины, определяется площадью рамки. Кроме этого он понял, что рамки надо не изготавливать самостоятельно, а покупать в специальном магазине. Заглянув в прайс-лист магазина, он увидел, что для каждой рамки в нем указаны длины внешних сторон и ширина.
Поясним подробнее то, как выглядит треугольная рамка. Ее изготовление происходит следующим образом: берется доска из красного дерева, имеющая форму треугольника со сторонами a, b и c. После этого стороны этого треугольника мысленно сдвигаются внутрь него на расстояние d (измеряемое по перпендикуляру к соответствующей стороне). На точках пересечения «сдвинутых» сторон строится маленький треугольник, который затем вырезается из исходного. Пример рамки со сторонами a = 6, b = 8, c = 10 и шириной d = 1 показан на рисунке.
Помогите художнику по имеющимся в прайс-листе данным вычислить площадь рамки.
Входные данные
На вход программы поступают четыре целых числа a, b, c, d ( 1
a, b, c, d1000) – длины внешних сторон рамки и ее ширина, соответственно. Гарантируется, что треугольник со сторонами a, b и c существует, и что в треугольнике есть точка, расстояние от которой до ближайшей стороны строго больше d.
Выходные данные
Выведите площадь рамки с точностью не меньше 10-5.
Примеры
Входные данные
6 8 10 1
Выходные данные
18.0
#416
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
64 megabytes
Во Флатландии n городов, расположенных в различных точках плоскости. Известно, что никакие три города не лежат на одной прямой.
Правительство решило построить в стране сеть сверхскоростных шоссе. Сеть шоссе должна быть такой, чтобы из любого города можно было проехать в любой другой по построенным шоссе. А в целях экономии средств было решено, что путь, соединяющий любые два города, должен быть единственным. Каждое шоссе представляет собой отрезок, соединяющий некоторую пару городов.
Завод, выполняющий этот госзаказ, подготовил проект сети шоссе. Проект представляет собой описание n - 1 шоссе. Каждое шоссе задается городами, которые оно соединяет. В целях секретности вместо названий городов в проекте были использованы коды – числа от 1 до n.
Однако когда дело дошло до реализации проекта, выяснилось, что документ, в котором было указано соответствие номеров городам, утерян. Поскольку проект приурочен к пятисотлетию культурной столицы Флатландии, переделывать проект полностью оказалось невозможно. Поэтому было решено установить некоторое новое соответствие номеров городам.
При попытке это сделать разработчики проекта столкнулись со следующей проблемой. В соответствии с техническими нормами строительства, недопустимо, чтобы шоссе пересекались вне городов. Поэтому не любое сопоставление номеров городам допустимо. После пары бессонных ночей главный инженер завода решил поручить спасение проекта вам.
Ваша задача – таким образом сопоставить числам от 1 до n города, чтобы после реализации проекта шоссе не пересекались вне городов, которые они соединяют.
Входные данные
В первой строке вводится целое число n – количество городов во Флатландии ( 2n1500).
Далее следует n описаний городов. Описание каждого города состоит из двух строк. Первая строка содержит название города – строку, состоящую из символов с ASCII-кодами от 33 до 127. Названия различных городов не совпадают. Длина названия города не превышает 60 символов. Вторая строка описания города содержит два целых числа x и y – координаты города. Координаты не превышают 104 по абсолютной величине.
Далее следуют n - 1 строк, которые описывают проект строительства сети шоссе в его текущем состоянии. Каждая строка содержит по два целых числа – номера городов, соединенных шоссе в проекте. Никакое шоссе в проекте не соединяет город сам с собой, никакие два города не соединены более, чем одним шоссе.
Выходные данные
Выведите n строк, i-я из этих строк должна содержать название города, который следует сопоставить числу i в проекте. Если решений несколько, выведите любое.
Если решения не существует, выведите строку «No solution».
Примеры
Входные данные
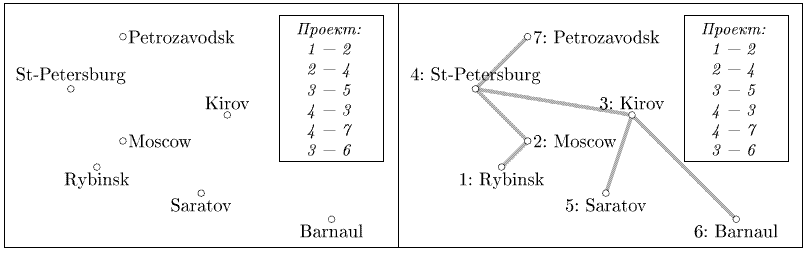
7 Moscow 2 2 St-Petersburg 0 4 Kirov 6 3 Saratov 5 0 Rybinsk 1 1 Petrozavodsk 2 6 Barnaul 10 -1 1 2 2 4 3 5 4 3 4 7 3 6
Выходные данные
St-Petersburg Rybinsk Kirov Saratov Moscow Petrozavodsk Barnaul
Выбрано
:
|