Вася с Петей играют в интересную игру. Правила ее очень простые: есть две рамки и участники должны передвинуть вторую рамку так, что площадь пересечения рамок была бы как можно большой. Оба игрока думают в течение минуты и записывают вектор переноса второй рамки. Побеждает тот игрок, чей вектор переноса дал большую площадь пересечения.
Игра имеет много частных случаев, так что Вася решил сжульничать и написать программу, находящую лучший вектор переноса.
В этой игре рамкой называется фигура, состоящая из двух прямоугольников: внешнего и внутреннего. Внутренний прямоугольник лежит строго внутри внешнего. Стороны обоих прямоугольников параллельны координатным осям.
На первом рисунке указаны (1) неправильные рамки, (2) правильные рамки, (3) пересечение рамок.
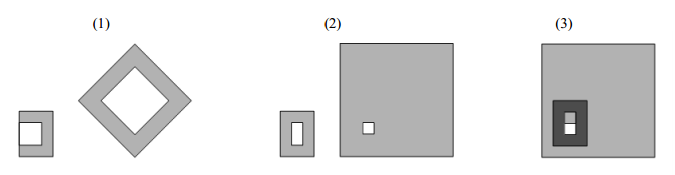
Площадь рамки вычисляется как W∙H – w∙h, где W, H – размеры внешнего прямоугольника, а w, h - размеры внутреннего (0 < w < W; 0 < h < H).
Напишите программу, которая находит перенос одной рамки относительно другой, которая даст максимальную площадь пересечения.
Каждая рамка описывается с помощью четырех точек — двух противоположных углов внешнего прямоугольника и двух противоположных углов внутреннего прямоугольника. Точки описываются своими координатами x и y, которые являются целыми числами и не превосходят 108 по модулю.
В первой строке содержится описание первой рамки, во второй — второй.
Первая строка выходного файла должна содержать целое число A – максимальная площадь области пересечения данных рамок достижимая с помощью переноса.
Вторая строка должна содержать пару целых чисел x и y – координаты вектора переноса второй рамки который даст область пересечения A. Координаты не должны превосходить 1018 по абсолютному значению.
2 2 5 6 3 3 4 5 0 0 10 10 2 2 3 3
10 0 -4
Плоскость разбили на одинаковые прямоугольники размера \(M\times N\) со сторонами, параллельными осям координат, и вершинами, расположенными в точках (\(M\times i, N\times j\)), где \(i\) и \(j\) пробегают всевозможные целые числа. Пусть на этой плоскости задана точка \(P(x,y)\) с целочисленными координатами. Назовем расстоянием от точки \(P\) до некоторого прямоугольника наименьшее из расстояний от \(P\) до точек этого прямоугольника, включая его границу. В частности, расстояние от точки до прямоугольника, в котором она содержится, равно 0.
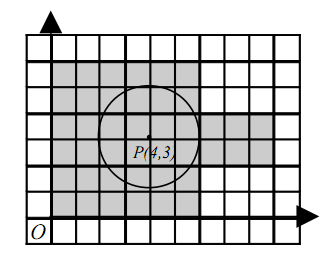 Требуется написать программу, перечисляющую прямоугольники, удаленные от \(P\) на расстояние, не превосходящее \(L\). Прямоугольники должны быть перечислены в порядке неубывания этого расстояния.
Требуется написать программу, перечисляющую прямоугольники, удаленные от \(P\) на расстояние, не превосходящее \(L\). Прямоугольники должны быть перечислены в порядке неубывания этого расстояния.
Во входном файле содержатся целые числа \(M\), \(N\), \(L\), \(x\) и \(y\) (\(1 \leq M\leq 10\), \(1 \leq N\leq 10\), \(0\leq L\leq 1000\), \(–30000 \leq x,y \leq 30000\)), разделенные пробелами и/или переводами строк.
Выведите в выходной файл координаты левых нижних углов искомых прямоугольников в описанном выше порядке. Прямоугольники, равноудаленные от \(P\), могут выводиться в произвольном порядке.
3 2 2 4 3
7
Недавно админ Вася настраивал компьютеры, в отделе Инопланетных объектов, увидел на столе спутниковый снимок с одной из недавно разведанных планет. На снимке было изображено необычное поле, разбитое на правильные шестиугольники, причем кто-то из ученых уже занумеровал все шестиугольники определенным образом.

На некоторых позициях, находились странные сооружения - шестиугольные башни, испускающие лучи в направлениях 6 соседних клеток. В этот момент, к столу подошел один из работников отдела. Очевидно, заметив любопытство Васи, он решил рассказать ему о находке. Оказывается, что эти самые лучи при пересечении излучают энергию, и чем больше лучей пересекается в одной точке, тем больше энергии излучается. При этом лучи идут по прямой очень далеко(возможно даже уходят в бесконечность), но не могут проходить через препятствия, например другие сооружения.
Теперь ученые пытаются на основе этого открытия построить новый источник дешевой энергии, но для этого им нужно уметь находить для интересующей их точки, сколько лучей через нее проходят, и какие эмиттеры (странные шестиугольные сооружения) их излучают.
В первой строке указаны 3 числа n , r , c (1 ≤ n ≤ 10 5 , 0 ≤ r , c ≤ 10 9 ) - количество эмиттеров, и координаты интересующей ученых позиции. В следующих n строках указано по паре чисел r i , c i (0 ≤ r i , c i ≤ 10 9 ) , координаты i-ого эмиттера. Гарантируется, что никакие два эмиттера не находятся в одной точке, и никакой эмиттер не находится в интересующей ученых точке.
В первой строчке выходного файла выведите единственное число k — количество лучей проходящих через интересную точку.
В следующей строчке выведите k чисел, номера эмиттеров, излучающих эти лучи, в произвольном порядке(все эмиттеры занумерованы с 1)
4 2 2 0 0 0 3 2 1 3 3
2 3 2