Турнир Архимеда(52 задач)
Кировские командные турниры(8 задач)
Барнаульские командные турниры(10 задач)
Московская командная олимпиада(246 задач)
Командные чемпионаты школьников Санкт-Петербурга по программированию(167 задач)
ВКОШП(180 задач)
Рассмотрим фигуру, аналогичную показанной на рисунке (большой равносторонний треугольник, составленный из маленьких равносторонних треугольников). На рисунке приведена фигура, состоящая из 4-х уровней треугольников.
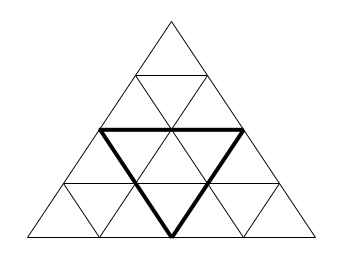
Напишите программу, которая будет определять, сколько всего в ней треугольников (необходимо учитывать не только "маленькие" треугольники, а вообще все треугольники — в частности, треугольник, выделенный жирным, а также вся фигура, являются интересующими нас треугольниками).
Вводится одно число \(N\) — количество уровней в фигуре (\(1\le N \le 100000\)).
Выведите количество треугольников в такой фигуре.
1
1
2
5
4
27
Петя - большой любитель математических головоломок. Недавно он прочитал в одном популярном журнале о новой головоломке. Он пытался ее решить несколько дней, но это ему так и не удалось. Помогите Пете справиться с неподдающейся задачей.
В ряд выписаны n чисел. Требуется поставить между каждой парой соседних чисел один из знаков "+" или "×" таким образом, чтобы значение получившегося выражения было как можно больше. Использовать скобки не разрешается.
Например, для последовательности чисел 1, 2, 3, 1, 2, 3 оптимально расставить знаки следующим образом: 1 + 2 × 3 × 1 × 2 × 3. Значение выражения в этом случае равно 37.
В первой строке вводится число \(n\) (2 <= \(n\) <= 200000). Вторая строка содержит \(n\) целых чисел - числа, между которыми следует расставить знаки. Все числа находятся в диапазоне от 0 до \(10^9\).
Выведите оптимальное выражение. В качестве знака "×" выводите символ "*" (звездочку). Если оптимальных решений несколько, выведите любое из них.
6 1 2 3 1 2 3
1+2*3*1*2*3
В правильном N-угольнике провели некоторые диагонали так, что он оказался разбит на треугольники. Изначально стороны N-угольника и все его диагонали черные.
Разрешается выбрать четырехугольник, в котором ровно одна диагональ, и при этом эта диагональ черного цвета (сам четырехугольник не обязан быть полностью черным) и проделать с ним следующее: заменить диагональ на противоположную (т.е. если сам четырехугольник был ABCD и в нем была диагональ AC, то она меняется на диагональ BD), после чего перекрасить стороны этого четырехугольника и новую диагональ в красный цвет.
Требуется определить, можно ли с помощью таких операций сделать так, чтобы все отрезки (т.е. стороны N-угольника и изображенные диагонали) стали красными, и не осталось бы ни одного черного отрезка. А если это возможно, то какое минимальное количество операций для этого требуется.
Вводится сначала число N (3≤N≤30000). Далее идет описание N–3 проведенных диагоналей. Каждая диагональ описывается двумя натуральными числами — номерами вершин, которые она соединяет. Гарантируется, что проведенные диагонали внутри N-угольника не пересекаются.
Выведите минимальное число действий, необходимое для того, чтобы перекрасить весь N-угольник и все его диагонали. Если перекрасить многоугольник указанным способом невозможно, выведите одно число –1 (минус один).
Примеры
| Входные данные | Выходные данные |
| 3 | –1 |
| 4 1 3 | 1 |
Требуется заполнить N элементов массива, пронумерованных числами от 1 до N (A[1]…A[N]), натуральными числами от 2 до N+1, использовав каждое число ровно один раз, так, чтобы значение каждого элемента массива делилось бы нацело на его номер (т.е. для каждого i A[i] делилось бы на i).
Напишите программу, которая для заданного N вычислит количество способов такого заполнения массива.
Вводится одно натуральное число N (1≤N≤60000).
Выведите одно число — искомое количество способов заполнения массива.
Пример
| Входные данные | Выходные данные | Комментарии |
| 2 | 1 | Массив можно заполнить единственным способом: 3 2 |
Региональное отделение одного крупного банка заказало два несгораемых шкафа для хранения личных дел своих клиентов. Каждый шкаф имеет несколько ящиков различной высоты, при просмотре снизу вверх ящики в первом шкафу имеют высоту a1, a2, ..., am, а ящики во втором шкафу высоту b1, b2, ..., bn.
Шкафы были установлены в узкой нише в стене лицевой стороной друг к другу, поэтому оказалось, что выдвинуть одновременно два ящика, находящиеся напротив друг друга, невозможно. Сотрудники банка постоянно обращаются к личным делам клиентов, поэтому им удобнее держать ящики открытыми в течение рабочего дня. Поскольку пока клиентов у банка немного, использовать все ящики не обязательно. Решено было использовать такое множество ящиков, чтобы их все можно было выдвинуть одновременно и они не мешали друг другу. Чтобы максимально систематизировать работу, необходимо использовать как можно больше ящиков.
Помогите сотрудникам банка выбрать, какие ящики следует использовать.
Первая строка входного файла содержит два целых числа: m и n — количество ящиков в первом и во втором шкафу, соответственно (1 ≤ m, n ≤ 100000). Вторая строка содержит m целых чисел: a1, a2, ..., am высоты ящиков в первом шкафу. Третья строка содержит n целых чисел: b1, b2, ..., bn — высоты ящиков во втором шкафу. Высоты ящиков положительные и не превышают 109.
На первой строке входного файла выведите два числа k и l количество ящиков, которые следует использовать в первом и втором шкафу, соответственно. Сумму k + l вам следует максимизировать. На второй строке выведите k целых чисел номера ящиков в первом шкафу, которые следует использовать. На третьей строке выведите l целых чисел номера ящиков во втором шкафу, которые следует использовать. Если оптимальных решений несколько, выведите любое.
5 5 1 2 3 4 5 6 4 3 2 1
4 3 1 2 3 4 3 4 5