Путешествие по стране никогда не бывает простым, особенно когда не существует прямого сообщения между городами. Группа туристов хочет добраться в город Метрополис, используя сеть железных дорог, которая соединяет n городов, пронумерованных от 1 до n. Город, из которого выезжает группа, имеет номер 1, Метрополис имеет номер n.
На железной дороге постоянно функционируют m маршрутов поездов. Каждый маршрут определяется последовательностью городов, перечисленных в том порядке, в каком их проезжает поезд, обслуживающий этот маршрут. В каждом маршруте для каждой пары соседних городов задано время, за которое поезд этого маршрута проезжает перегон между этими городами. При этом поезда разных маршрутов могут проезжать один и тот же перегон за разное время.
По пути в Метрополис группа может садиться на поезд и сходить с поезда в любом городе маршрута, не обязательно в начальном или конечном. При этом, можно сойти с поезда маршрута i, пересесть на поезд маршрута j, возможно сделать еще несколько пересадок, а потом вновь сесть в поезд того же маршрута i.
Туристы предъявляют высокие требования к выбору способа проезда в Метрополис.
Во-первых, суммарное время, проведенное в поездах, должно быть минимальным.
Во-вторых, среди всех способов с минимальным временем нахождения в поездах предпочтительным является тот способ, для которого сумма квадратов промежутков времени, непрерывно проведенных в поезде между двумя пересадками, максимальна. Назовём эту сумму качеством путешествия.
Время, проведенное вне поездов, не учитывается.
Требуется написать программу, которая по описаниям имеющихся маршрутов поездов определит минимальное время, которое группе туристов придется провести в поездах, а также максимальное качество путешествия с таким временем.
Выходные данные
Выходные данные должны содержать два целых числа — минимальное суммарное время, которое придется провести в поездах, и максимальное качество пути с таким временем.
Примечание
В первом примере группа туристов отправится прямым маршрутом в Метрополис.
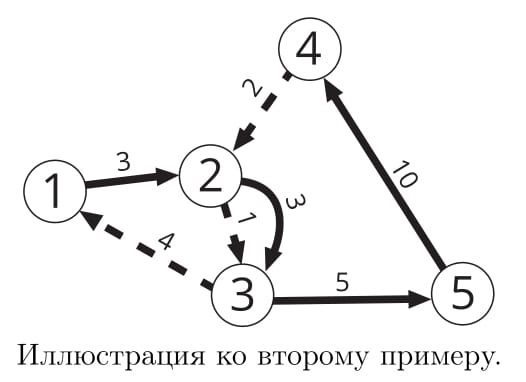
Во втором примере не оптимально проехать напрямую по первому маршруту, так как время в поезде при этом не будет минимальным возможным. Поэтому они отправятся на поезде по маршруту 1 из города 1 в город 2, затем на поезде по маршруту 2 из города 2 в город 3, а затем снова на поезде по маршруту 1 из города 3 в город 5. При этом сумма квадратов промежутков времени, проведенных в поездах между пересадками, равна 32 + 12 + 52 = 35.
В третьем примере добраться из города 1 в город 4 за минимальное время можно, пересаживаясь с маршрута 1 на маршрут 2 в любом из городов 2, 3 или 4. Максимальное качество путешествия достигается при пересадке в городе 2: 12 + 92 = 82.
Обратите внимание, что второй и третий примеры не удовлетворяют ограничениям первой и второй подзадачи, решение будет протестировано на этих подзадачах, если оно пройдет первый тест из примера. Все тесты из примера подходят под ограничения подзадач 3 – 7, решение будет проверяться на тестах этих подзадач только в случае прохождения всех тестов из примера.

