#113544

Темы: [Стек] [Интерактивные задачи]

Источники: [ Личные олимпиады, Всероссийская олимпиада школьников, Заключительный этап, 2017, 1 день, Программирование квадрокоптеров ]

Школьники готовятся к участию в соревновании по программированию квадрокоптеров. Квадрокоптер, который используется в соревновании, может выполнять две команды: подняться вверх на 1 метр и опуститься вниз на 1 метр. Команда подъёма обозначается символом «(», а команда спуска — символом «)».

Программа для квадрокоптера представляет собой последовательность команд. Программа считается корректной, если, начав её исполнение на уровне земли и выполнив последовательно все команды, квадрокоптер снова оказывается на уровне земли. При этом в процессе выполнения программы квадрокоптер не должен пытаться опуститься ниже уровня земли.

Например, следующие программы являются корректными: «()(())», «((()))». Программа«(((» не является корректной, поскольку квадрокоптер завершает ее выполнение на высоте 3 метра над уровнем земли, программа «())(» также не является корректной, поскольку при выполнении третьей команды квадрокоптер пытается опуститься ниже уровня земли.

Участник соревнования написал корректную программу для квадрокоптера, состоящую из n команд, пронумерованных от 1 до n. Он загрузил её в память квадрокоптера для демонстрации во время соревнования. К сожалению, после загрузки программы в память квадрокоптера участник случайно удалил её на своём компьютере, а квадрокоптер не позволяет выгрузить программу из своей памяти.

К счастью, квадрокоптер поддерживает специальный режим отладки программы. В этом режиме квадрокоптер с загруженной в него программой может отвечать на специальные запросы. Каждый запрос представляет собой два целых числа: l и r, 1 ≤ l ≤ r ≤ n. В ответ на запрос квадрокоптер сообщает, является ли фрагмент загруженной в него программы, состоящий из команд с l-й по r-ю включительно, корректной программой для квадрокоптера, либо нет. Участник хочет с помощью режима отладки восстановить загруженную в квадрокоптер программу.

Требуется написать программу-решение, которая взаимодействует с программой жюри, моделирующей режим отладки квадрокоптера, и в итоге восстанавливает загруженную в квадрокоптер программу.

Протокол взаимодействия

Это интерактивная задача.

Сначала на вход подаётся целое число n — количество команд в программе квадрокоптера (2 ≤ n ≤ 50 000).

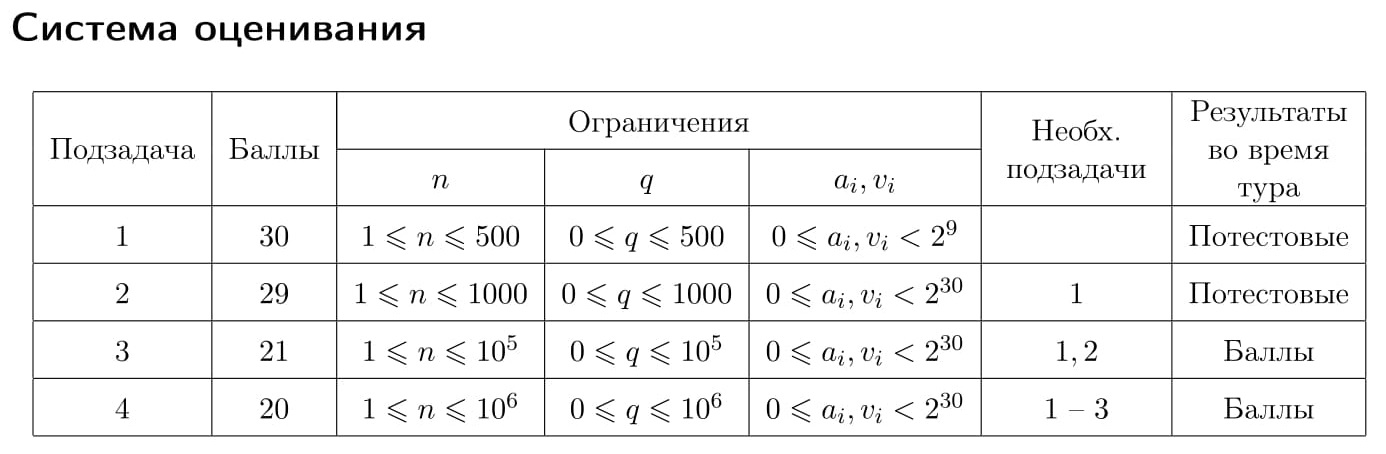
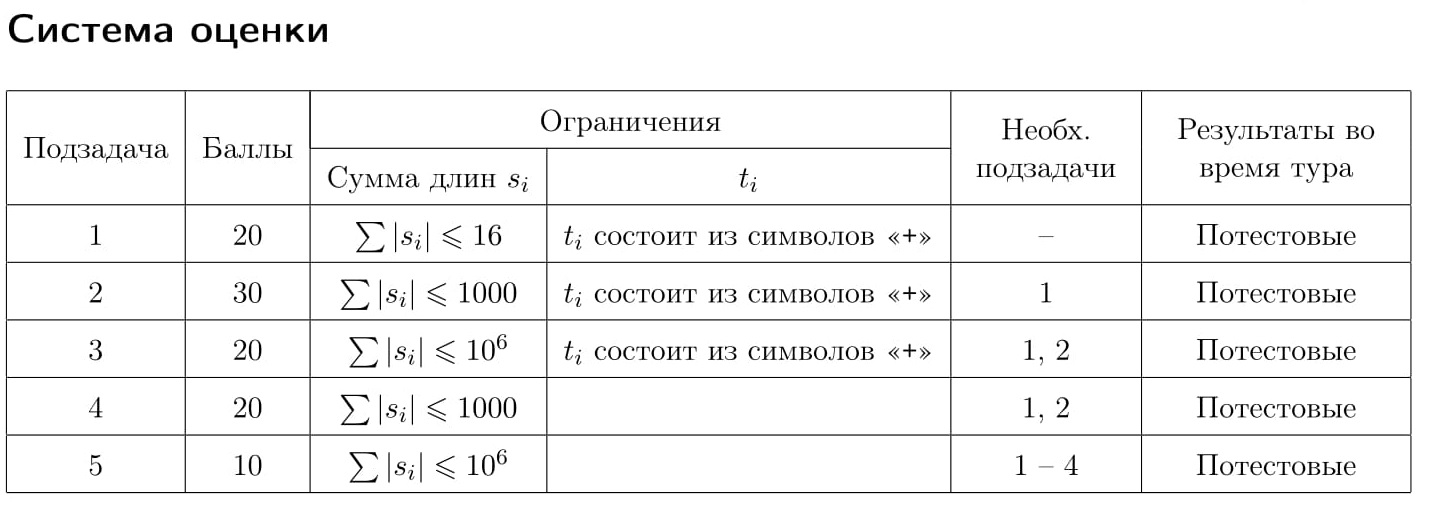
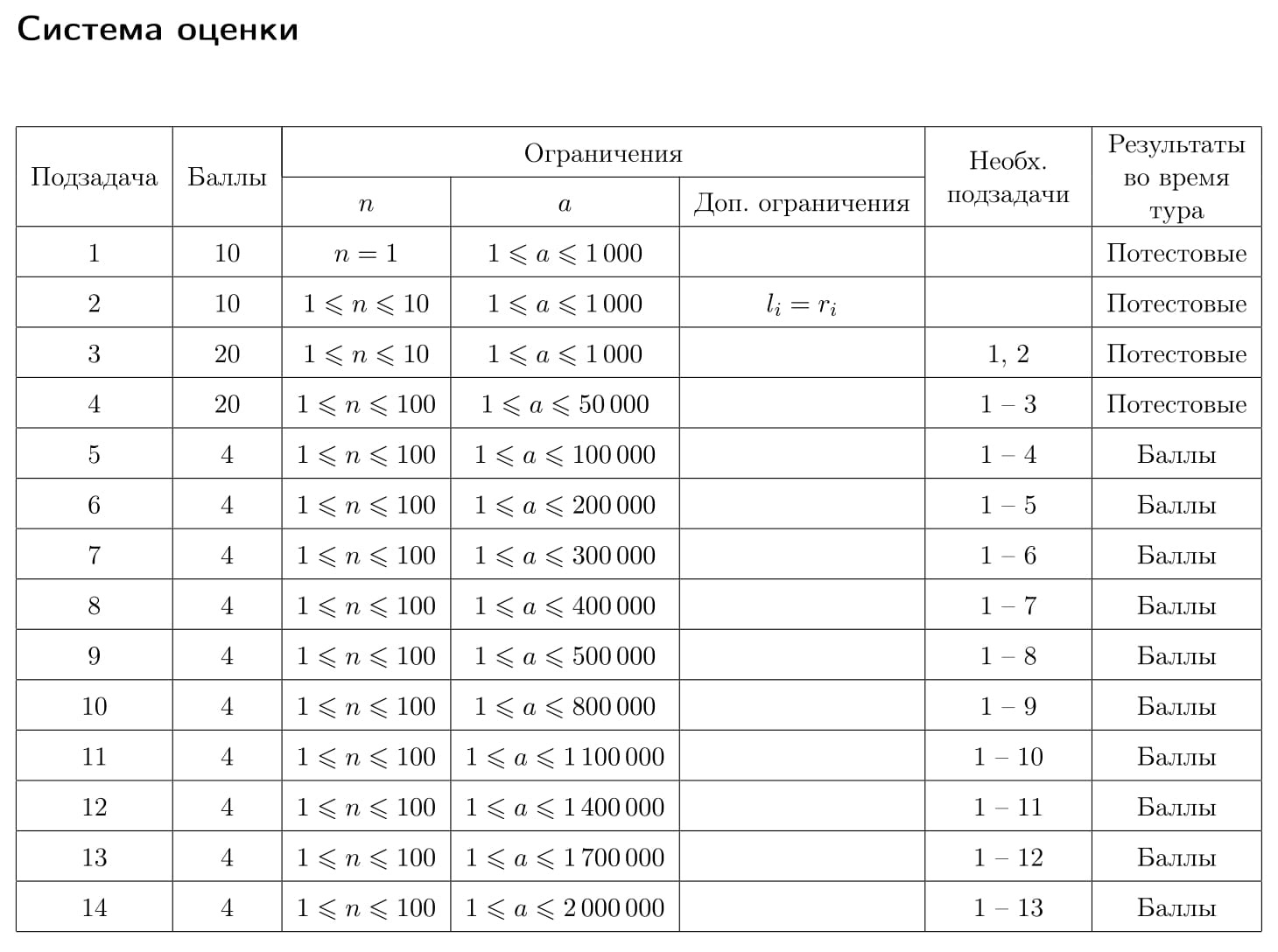
Для каждого теста жюри зафиксировано число k — максимальное количество запросов. Гарантируется, что k запросов достаточно, чтобы решить задачу. Это число не сообщается программе-решению. Ограничения k в различных подзадачах приведены в таблице системы оценивания. Если программа-решение делает более k запросов к программе жюри, то на этом тесте она получает в качестве результата тестирования «Неверный ответ».

Чтобы сделать запрос, программа-решение должна вывести строку вида «? l r», где l и r — целые положительные числа, задающие фрагмент программы квадрокоптера (1 ≤ l ≤ r ≤ n).

В ответ на запрос программы-решения программа жюри подаёт ей на вход либо строку «Yes», либо строку «No», в зависимости от того, является ли запрошенный фрагмент программы квадрокоптера корректной программой.

Если программа-решение определила ответ на задачу, то она должна вывести строку «! c_1c₂... c_n», где символ c_i задаёт i-ю команду в программе квадрокоптера и равен либо «(», либо «)».

После этого программа-решение должна завершиться.

Гарантируется, что в каждом тесте программа в памяти квадрокоптера является фиксированной корректной программой, которая не меняется в зависимости от запросов, произведённых программой-решением.

Приведённые примеры иллюстрируют взаимодействие программы-решения с программой жюри «по шагам», для чего в них добавлены дополнительные пустые строки. При реальном тестировании лишние пустые строки вводиться не будут, выводить пустые строки также не требуется.

В первом примере n = 4. Единственная возможная корректная программа из двух команд это «()», поэтому из результатов третьего и четвёртого запросов можно сделать вывод, что программа в памяти квадрокоптера — «()()». Поэтому, в частности, ответ на второй запрос действительно «No», так как фрагмент программы «()(» не является корректной программой: если квадрокоптер исполнит именно эти три команды, он останется на уровне одного метра над землёй.

В втором примере n = 6, и произведённых запросов достаточно, чтобы однозначно определить, что программа в памяти квадрокоптера — «((()))».

В тестах из условия k = 150, то есть, разрешается произвести не более 150 запросов.

#113545

Иллюзия сортировки

Темы: [Дерево отрезков, RSQ, RMQ]

Источники: [ Личные олимпиады, Всероссийская олимпиада школьников, Заключительный этап, 2017, 1 день, Иллюзия сортировки ]

Известный программист пробует себя в роли иллюзиониста. Его коронный фокус состоит в следующем.

Для заданного массива из n целых неотрицательных чисел a₁, a₂, ..., a_n он быстро подбирает магическое число b. Целое неотрицательное число b называется магическим для массива, если применение операции побитового исключающего ИЛИ с этим числом к каждому элементу массива превращает его в отсортированный массив. Иначе говоря,

\(\) (a_1\oplus b) \le (a_2\oplus b) \le ... \le (a_n\oplus b) \(\)

где \(\oplus\) — операция побитового исключающего ИЛИ.

Чтобы фокус был более эффектным, после предъявления магического числа для заданного массива иллюзионист q раз выполняет следующее действие. Он предлагает зрителям изменить один из элементов массива и после этого снова пытается предъявить магическое число. При этом программист настолько отточил свое мастерство иллюзиониста, что каждый раз предъявляет зрителям минимальное возможное магическое число. Иногда фокус не удаётся, так как для полученного массива невозможно подобрать магическое число.

Требуется написать программу, которая по заданному исходно массиву, а также после каждого изменения элемента, вычисляет минимальное магическое число для полученного массива, либо определяет, что такого числа нет.

Примечание

Исключающее ИЛИ — это логическая операция, обозначаемая знаком \(\oplus\), которая задаётся следующей таблицей истинности:

Определим побитовое исключающее ИЛИ для двух неотрицательных целых чисел x и y. Запишем каждое из целых чисел x и y в двоичной системе счисления, дополнив при необходимости более короткое из чисел ведущими нулями до равной длины. Побитовое исключающее ИЛИ двух целых чисел \(x\) и \(y\), обозначаемое также как \(\oplus\), это целое неотрицательное число, каждый разряд которого в двоичной системе счисления является исключающим ИЛИ соответствующих разрядов чисел \(x\) и \(y\). Например, \(5\oplus22=101_2\oplus10110_2=10011_2=19\).

Среди предложенных на олимпиаде языков программирования в языке Паскаль для обозначения исключающего ИЛИ используется оператор «xor», в остальных языках программирования используется оператор «^».

Входные данные

Первая строка входных данных содержит целое число n — количество чисел в массиве (1 ≤ n ≤ 10⁶).

Вторая строка содержит n целых чисел a₁, a₂, ..., a_n — элементы массива (0 ≤ a_i < 2³⁰).

Третья строка содержит целое число q — число изменений элемента массива (0 ≤ q ≤ 10⁶).

Следующие q строк содержат по два целых числа p_i и v_i, где p_i — номер элемента массива, который следует заменить (1 ≤ p_i ≤ n), а v_i — новое значение этого элемента (0 ≤ v_i < 2³⁰).

Выходные данные

Выходные данные должны содержать (q + 1) целых чисел b₀, b₁, ..., b_q, по одному в строке.

Значение b₀ — либо минимальное возможное магическое число для исходного массива, либо - 1, если такого числа не существует.

Для i от 1 до q значение b_i — либо минимальное возможное магическое число для массива после первых i изменений, либо - 1, если такого числа не существует.

Примеры

Входные данные

Выходные данные

#113548

Накопитель

Темы: [Стек]

Источники: [ Личные олимпиады, Всероссийская олимпиада школьников, Заключительный этап, 2017, 2 день, Накопитель ]

Исследуется новое цифровое устройство для хранения информации. Информация на устройстве хранится в виде последовательности ячеек, каждая из которых находится в одном из двух состояний, обозначаемых символами «+» и «-», и, таким образом, хранит один бит информации.

Назовём фрагментом группу соседних ячеек с одинаковым состоянием, слева от которой либо нет ячеек, либо находится ячейка в противоположном состоянии, и справа — либо нет ячеек, либо находится ячейка в противоположном состоянии.

Операция записи позволяет выбрать любую пару соседних фрагментов разной длины и изменить состояние всех ячеек более короткого фрагмента на противоположное, объединяя таким образом два или три соседних фрагмента в один.

Требуется написать программу, которая по заданной исходной и итоговой последовательностям состояний ячеек определяет, можно ли из исходной последовательности получить итоговую с помощью последовательных операций записи.

Входные данные

Первая строка входных данных содержит целое положительное число q — количество тестов.

Каждая из следующих q строк содержит s_i, t_i — непустые последовательности символов «+» и «-» одинаковой длины, разделённые одним пробелом. Эта строка означает, что в тесте номер i из исходной последовательности состояний ячеек s_i требуется получить итоговую последовательность t_i.

Выходные данные

Выходные данные должны содержать q строк, где i-я строка равна «Yes», если из исходной последовательности состояний ячеек s_i можно получить итоговую последовательность t_i, или «No» в противном случае.

Примеры

Входные данные

3
++- +++
++-- ++++
++-+--+- ++++++++

Выходные данные

Yes
No
Yes

Входные данные

3
++-+-- ++----
++-+-- +++---
-++- -++-

Выходные данные

Yes
No
Yes

#113550

Антивещество

Темы: [Динамическое программирование] [Дерево отрезков, RSQ, RMQ] [Система непересекающихся множеств] [Разреженные таблицы (sparse table)]

Источники: [ Личные олимпиады, Всероссийская олимпиада школьников, Заключительный этап, 2017, 2 день, Антивещество ]

Компания тестирует технологию получения антивещества, используемого в качестве топлива в межпланетном звездолёте. Антивещество получается в результате специальных экспериментов в реакторе.

Известно n типов экспериментов, приводящих к получению антивещества. В результате проведения эксперимента i-го типа в выходной контейнер реактора добавляется от l_i до r_i граммов антивещества. Из соображений безопасности запрещается накапливать в контейнере более a граммов антивещества.

Затраты на проведение эксперимента i-го типа составляют c_i, а стоимость одного грамма полученного антивещества составляет 10⁹.

Если после проведения экспериментов в контейнере образовалось t граммов антивещества, а суммарные затраты на проведение экспериментов в реакторе составили s, то прибыль определяется по формуле (t·10⁹ - s). Компании необходимо разработать стратегию проведения экспериментов, позволяющую максимизировать прибыль, которую можно гарантированно получить.

В зависимости от результатов предыдущих экспериментов стратегия определяет, эксперимент какого типа следует провести, или решает прекратить дальнейшее выполнение экспериментов. Стратегия позволяет гарантированно получить прибыль x, если при любых результатах проведения экспериментов: во-первых, в контейнере реактора оказывается не более a граммов антивещества, во-вторых, прибыль составит не менее x.

Например, пусть возможен только один тип эксперимента, порождающий от 4 до 6 граммов антивещества, затраты на его проведение равны 10, а вместимость контейнера составляет 17 граммов. Тогда после двукратного проведения эксперимента в контейнере может оказаться от 8 до 12 граммов антивещества. Если получилось 12 граммов, то больше проводить эксперимент нельзя, так как в случае получения 6 граммов антивещества контейнер может переполниться. В остальных случаях можно провести эксперимент в третий раз и получить от 12 до 17 граммов антивещества. В худшем случае придётся провести эксперимент трижды, затратив в сумме 30, прибыль составит (12·10⁹ - 30) = 11 999 999 970.

Требуется написать программу, которая определяет максимальную прибыль x, которую гарантированно можно получить.

Входные данные

Первая строка входных данных содержит два целых числа: n — количество типов экспериментов и a — максимально допустимое количество антивещества в контейнере (1 ≤ n ≤ 100, 1 ≤ a ≤ 2 000 000).

Следующие n строк содержат по три целых числа l_i, r_i и c_i — минимальное и максимальное количество антивещества, получаемое в результате эксперимента типа i, и затраты на эксперимент этого типа, соответственно (1 ≤ l_i ≤ r_i ≤ a, 1 ≤ c_i ≤ 100).

Выходные данные

Выходные данные должны содержать одно целое число — максимальную прибыль x, которую гарантированно можно получить.

Примеры

Входные данные

1 17
4 6 10

Выходные данные

11999999970

Входные данные

2 11
2 2 100
3 5 5

Выходные данные

9999999890

#113551

Траектория обучения

Темы: [Рекурсия] [Стек]

Источники: [ Личные олимпиады, Всероссийская олимпиада школьников, Заключительный этап, 2017, 2 день, Траектория обучения ]

Победитель студенческой олимпиады получил предложения о стажировке от двух университетов. При подготовке планов обучения он узнал рейтинг качества преподавания каждой дисциплины в этих университетах.

Программа обучения первого университета состоит из последовательности перечисленных в хронологическом порядке n различных дисциплин a₁, a₂, ..., a_n, имеющих рейтинги x₁, x₂, ..., x_n соответственно. Программа обучения второго университета состоит из последовательности перечисленных в хронологическом порядке m различных дисциплин b₁, b₂, ..., b_m, имеющих рейтинги y₁, y₂, ..., y_m соответственно.

Студент имеет возможность составить план обучения в первом университете таким образом, чтобы изучить дисциплины на позициях учебной программы с l_a по r_a включительно (1 ≤ l_a ≤ r_a ≤ n), либо отказаться от стажировки в первом университете. Аналогично он может составить план обучения во втором университете таким образом, чтобы изучить дисциплины на позициях учебной программы с l_b по r_b включительно (1 ≤ l_b ≤ r_b ≤ m), либо отказаться от стажировки во втором университете.

Изучать одну и ту же дисциплину дважды в разных университетах не имеет смысла, поэтому все дисциплины в двух выбранных планах обучения должны быть различны.

Требуется написать программу, которая определит планы обучения студента таким образом, чтобы получить наибольшую возможную сумму рейтингов изучаемых дисциплин.

Входные данные

Первая строка входных данных содержит целые числа n и m — количество дисциплин в программах обучения первого и второго университетов (1 ≤ n, m ≤ 500 000).

Вторая строка входных данных содержит n целых чисел a_i — дисциплины, входящие в программу обучения первого университета, перечисленные в хронологическом порядке (1 ≤ a_i ≤ n + m).

Третья строка входных данных содержит n целых чисел x_i — рейтинги дисциплин, входящих в программу обучения первого университета, перечисленные том же порядке, что и дисциплины a_i (1 ≤ x_i ≤ 10⁹).

Четвёртая строка входных данных содержит m целых чисел b_i — дисциплины, входящие в программу обучения второго университета, перечисленные в хронологическом порядке (1 ≤ b_i ≤ n + m).

Пятая строка входных данных содержит m целых чисел y_i — рейтинги дисциплин, входящих в программу обучения второго университета, перечисленные том же порядке, что и дисциплины b_i (1 ≤ y_i ≤ 10⁹).

Выходные данные

Первая строка выходных данных должна содержать целое число r — наибольшую возможную сумму рейтингов дисциплин.

Вторая строка выходных данных должна содержать целые числа l_a, r_a — позиции в учебной программе первой и последней дисциплин, входящих в план обучения в первом университете, либо «0 0», если студент отказался от стажировки в первом университете.

Третья строка выходных данных должна содержать целые числа l_b, r_b — позиции в учебной программе первой и последней дисциплин, входящих в план обучения во втором университете, либо «0 0», если студент отказался от стажировки во втором университете.

Если возможных правильных ответов несколько, разрешается вывести любой из них.

Примечание

В первом тесте из условия приведённые планы обучения в университетах приводят к суммарному рейтингу дисциплин (7 + 4 + 10 + 1 + 5) + (5 + 3 + 4) = 27 + 12 = 39. Если бы студент выбрал только вторую и третью дисциплины в первом университете и весь курс обучения во втором университете, суммарный рейтинг дисциплин был бы (7 + 4) + (3 + 5 + 3 + 4 + 12) = 11 + 27 = 38.

Во втором тесте из условия первая и третья дисциплины во втором университете имеют настолько высокий рейтинг по сравнению с соответствующими дисциплинами первого университета, что наиболее выгодный вариант — пройти целиком стажировку во втором университете и отказаться от стажировки в первом университете.

Примеры

Входные данные

7 5
3 1 4 8 6 9 2
2 7 4 10 1 5 3
9 2 11 3 8
3 5 3 4 12

Выходные данные

39
2 6
2 4

Входные данные

Выходные данные

34
0 0
1 3

Входные данные

Выходные данные

19
1 1
3 3