Страница: << 6 7 8 9 10 11 12 >> Отображать по:

#111494

Две окружности

Темы: [Элементарная геометрия]

Источники: [ Личные олимпиады, Всероссийская олимпиада школьников, Региональный этап, 2013, 2 день, Задача C ]

Юный футболист Митя обнаружил на школьном футбольном поле две различные окружности, нарисованные едва заметной белой краской. Вспомнив истории о загадочных кругах на полях, он отметил эти окружности с помощью небольших камушков. Митя разложил на поле n камушков так, чтобы каждый из них находился на одной из окружностей или даже на их пересечении, если эти окружности пересекаются. Получилось так, что на каждой окружности размещался хотя бы один камушек. Обладая великолепным глазомером, Митя расположил камушки на окружностях абсолютно точно, без какой-либо погрешности.

На следующий день пошел дождь, краска стерлась, и нарисованные окружности исчезли, но все камушки остались на своих местах. Теперь Мите очень нужно найти доказательство необычного явления, свидетелем которого он был, то есть, восстановить окружности.

Требуется написать программу, которая по координатам камушков на поле находит вариант размещения их на двух несовпадающих окружностях.

Входные данные

Первая строка входного файла содержит целое число n — количество размещенных Митей камушков на поле ($2 \leq n \leq 2000$). Последующие n строк содержат целочисленные координаты ($x_i$, $y_i$) камушков — по одной паре координат, разделенных пробелом, в каждой строке ($−10^6 \leq x_i, y_i \leq 10^6$). Никакие два камушка не размещаются в одной точке.

Гарантируется, что ответ для заданного набора камушков существует.

Выходные данные

Выходной файл должен содержать две строки. Первая строка должна содержать последовательность номеров всех камушков, которые принадлежат первой окружности, вторая строка — последовательность номеров всех камушков, которые принадлежат второй окружности.

Каждый камушек должен встречаться хотя бы в одной из двух последовательностей. Если камушек встречается в обеих последовательностях, то это обозначает, что он находится на пересечении окружностей. Считается, что камушки пронумерованы от 1 до n в порядке их следования во входных данных.

Нумерация окружностей не имеет значения, то есть выводить две последовательности можно в любом порядке. Числа в последовательностях можно также выводить в произвольном порядке. Каждая из последовательностей должна содержать не менее одного числа. Все числа в строках должны быть разделены пробелами.

Если вариантов расположения окружностей несколько, можно выбрать любой из них.

Система оценивания

Правильные решения для тестов, в которых 2 ≤ n ≤ 50, будут оцениваться из 50 баллов.

Примеры

Входные данные

Выходные данные

1 2 3 6 
4 5 6 7

Входные данные

Выходные данные

1 2 3 4 
5

#111495

Столицы

Темы: [Динамическое программирование на графах] [Обход в глубину]

Источники: [ Личные олимпиады, Всероссийская олимпиада школьников, Региональный этап, 2013, 2 день, Задача D ]

В стране Триландии близятся выборы новых столиц. Столицы в Триландии необычные, поскольку ими являются одновременно сразу три различных города. Такая идея размещения столиц основана на исследованиях эффективности управления страной, выполненных ведущими экономистами Триландии.

Всего в Триландии n городов, из которых некоторые пары городов соединены дорогами, и по каждой из них можно проехать в обе стороны. Время проезда по каждой дороге в одну сторону равно одному часу. При этом все города соединены дорогами таким образом, что из каждого города можно добраться в любой другой, причем это можно сделать единственным способом, если по каждой дороге проезжать не более одного раза и только в одну сторону.

Как показали результаты проведенных триландскими экономистами исследований, управление страной будет наиболее эффективным, если три столицы будут выбраны так, что время кратчайшего пути между каждой парой столиц составит ровно d часов. Перед проведением выборов необходимо знать, сколько существует различных троек городов, удовлетворяющих описанным выше свойствам. Две тройки городов считаются различными, если в первой тройке есть хотя бы один город, которого нет во второй тройке, и наоборот.

Требуется написать программу, которая по количеству городов в Триландии и описанию дорог находит количество троек городов, которые могут быть столицами.

Входные данные

Первая строка входного файла содержит два разделенных пробелом целых числа: количество городов в Триландии n и требуемое время в пути между столицами d ($3 \leq n \leq 10^5$, $1 \leq d < n$). Каждая из последующих (n – 1) строк содержит описание одной дороги: пару разделенных пробелом различных целых чисел $a_i$ и $b_i$ — номера городов, которые соединены двусторонней дорогой ($1 \leq a_i \leq n$, $1 \leq b_i \leq n$, $a_i \ne b_i$). Каждая пара городов соединена не более чем одной дорогой.

Выходные данные

Выходной файл должен содержать одно целое число — количество подходящих троек городов, которые могут быть выбраны столицами. В случае, если нужных троек городов не окажется, выходной файл должен содержать ноль.

Пояснения к тестам

В первом примере существует единственный способ выбрать три столицы: города под номерами 2, 3 и 4. Рисунок, соответствующий первому примеру, приведен ниже.

$\text{[math]}$

Во втором примере существует четыре варианта выбора трёх столиц из четверки городов: 2, 3, 4 и 5. Можно также выбрать столицами города с номерами 1, 6 и 7. Рисунок, соответствующий второму примеру, приведен ниже.

$\text{[math]}$

Система оценивания

Правильные решения для тестов, в которых 3 ≤ n ≤ 50, будут оцениваться из 20 баллов.

Правильные решения для тестов, в которых 3 ≤ n ≤ 500, будут оцениваться из 40 баллов.

Правильные решения для тестов, в которых 3 ≤ n ≤ 5000, будут оцениваться из 60 баллов.

Примеры

Входные данные

Выходные данные

Входные данные

Выходные данные

#112038

Межрегиональная олимпиада

Темы: [Жадный алгоритм]

Источники: [ Личные олимпиады, Всероссийская олимпиада школьников, Региональный этап, 2014, 1 день, Задача C ]

На межрегиональной олимпиаде по программированию роботов соревнования проводятся в один тур и в необычном формате. Задачи участникам раздаются последовательно, а не все в самом начале тура, и каждая $i$-я задача (1 ≤ $i$ ≤ $n$) становится доступной участникам в свой момент времени $s_i$. При поступлении очередной задачи каждый участник должен сразу определить, будет он ее решать или нет. В случае, если он выбирает для решения эту задачу, то у него есть $t_i$ минут на то, чтобы сдать ее решение на проверку, причем в течение этого времени он не может переключиться на решение другой задачи. Если же участник отказывается от решения этой задачи, то в будущем он не может к ней вернуться. В тот момент, когда закончилось время, отведенное на задачу, которую решает участник, он может начать решать другую задачу, ставшую доступной в этот же момент, если такая задача есть, или ждать появления другой задачи. При этом за правильное решение $i$-й задачи участник получает $c_i$ баллов.

Артур, представляющий на межрегиональной олимпиаде один из региональных центров искусственного интеллекта, понимает, что важную роль на такой олимпиаде играет не только умение решать задачи, но и правильный стратегический расчет того, какие задачи надо решать, а какие пропустить. Ему, как и всем участникам, до начала тура известно, в какой момент времени каждая задача станет доступной, сколько времени будет отведено на ее решение и сколько баллов можно получить за ее решение. Артур является талантливым школьником и поэтому сможет успешно решить за отведенное время и сдать на проверку любую задачу, которую он выберет для решения на олимпиаде.

Требуется написать программу, которая определяет, какое максимальное количество баллов Артур сможет получить при оптимальном выборе задач, которые он будет решать, а также количество и перечень таких задач.

Формат входного файла

Первая строка входного файла содержит одно целое число $n$ (1 ≤ $n$ ≤ $10^5$) количество задач на олимпиаде.

Последующие $n$ строк содержат описания задач, по три числа на каждой строке: $s_i$ момент появления $i$-й задачи в минутах, $t_i$ время, отведенное на ее решение в минутах, и $c_i$ сколько баллов получит участник за решение этой задачи (1 ≤ $s_i$, $t_i$, $c_i$ ≤ $10^9$).

Формат выходного файла

Первая строка выходного файл должна содержать одно число – максимальное количество баллов, которое сможет получить Артур на олимпиаде.

Вторая строка должна содержать одно целое число $m$ - количество задач, которые надо решить при оптимальном выборе.

Третья строка должна содержать $m$ разделенных пробелом целых чисел - номера этих задач в порядке их решения. Задачи пронумерованы, начиная с единицы, в порядке их описания во входном файле.

Если оптимальных ответов несколько, необходимо вывести любой из них.

Пояснения к примерам

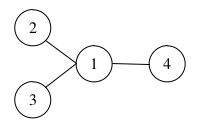
В первом примере Артур успевает решить все задачи и получить три балла.

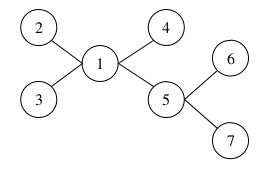
Во втором примере Артуру выгоднее решать последнюю задачу и получить за нее три балла, чем решать только первые две и получить два балла.

Система оценивания

Частичные правильные решения для тестов, в которых все $c_i$ одинаковы и $n$ ≤ 1000, оцениваются из 30 баллов.

Частичные правильные решения для тестов, в которых все $c_i$ одинаковы, оцениваются из 50 баллов.

Частичные правильные решения для тестов, в которых $n$ ≤ 1000, оцениваются из 50 баллов.

Примеры

Входные данные

2
1 1 1
2 2 2

Выходные данные

3
2
1 2

Входные данные

Выходные данные

3
1
3

#112041

Кондиционеры

Темы: [Сортировка подсчетом]

Источники: [ Личные олимпиады, Всероссийская олимпиада школьников, Региональный этап, 2014, 2 день, Задача B ]

При реализации проекта «Умная школа» было решено в каждый учебный класс выбранной для этого школы установить по кондиционеру нового поколения для автоматического охлаждения и вентиляции воздуха. По проекту в каждом классе должен быть установлен только один кондиционер и мощность кондиционера должна быть достаточной для размеров класса. Чем больше класс, тем мощнее должен быть кондиционер.

Все классы школы пронумерованы последовательно от 1 до $n$. Известно, что для каждого класса с номером $i$, требуется ровно один кондиционер, мощность которого больше или равна $a_i$ ватт.

Администрации школы предоставили список из $m$ различных моделей кондиционеров, которые можно закупить. Для каждой модели кондиционера известна его мощность и стоимость. Требуется написать программу, которая определит, за какую минимальную суммарную стоимость кондиционеров можно оснастить все классы школы.

Формат входного файла

Первая строка входного файла содержит одно целое число n (1 ≤ $n$ ≤ 50 000) количество классов в школе.

Вторая строка содержит $n$ целых чисел $a_i$ (1 ≤ $a_i$ ≤ 1000)- минимальная мощность кондиционера в ваттах, который можно установить в классе с номером $i$.

Третья строка содержит одно целое число $m$ (1 ≤ $m$ ≤ 50 000) - количество предложенных моделей кондиционеров.

Далее, в каждой из $m$ строк содержится пара целых чисел $b_j$ и $c_j$ (1 ≤ $b_j$ ≤ 1000, 1 ≤ $c_j$ ≤ 1000) мощность в ваттах $j$-й модели кондиционера и его цена в рублях соответственно.

Формат выходного файла

Выходной файл должен содержать одно число минимальную суммарную стоимость кондиционеров в рублях. Гарантируется, что хотя бы один корректный выбор кондиционеров существует, и во всех классах можно установить подходящий кондиционер.

Пояснения к примерам

В первом примере нужно купить один единственно возможный кондиционер за 1000 рублей.

Во втором примере оптимально будет установить в первом и втором классах кондиционеры четвертого типа, а в третьем классе – кондиционер третьего типа. Суммарная стоимость этих кондиционеров будет составлять 13 рублей (3 + 3 + 7).

Система оценивания

Частичные решения для $n$, $m$ ≤ 1000 будут оцениваться из 50 баллов.

Примеры

Входные данные

Выходные данные

Входные данные

Выходные данные

#112749

Вырубка леса

Темы: [Бинарный поиск по ответу]

Источники: [ Личные олимпиады, Всероссийская олимпиада школьников, Региональный этап, 2015, 2 день, Задача B ]

Фермер Николай нанял двух лесорубов: Дмитрия и Федора, чтобы вырубить лес, на месте которого должно быть кукурузное поле. В лесу растут $X$ деревьев.

Дмитрий срубает по A деревьев в день, но каждый $K$-й день он отдыхает и не срубает ни одного дерева. Таким образом, Дмитрий отдыхает в $K$-й, 2$K$-й, 3$K$-й день, и т.д.

Федор срубает по B деревьев в день, но каждый $M$-й день он отдыхает и не срубает ни одного дерева. Таким образом, Федор отдыхает в $M$-й, 2$M$-й, 3$M$-й день, и т.д.

Лесорубы работают параллельно и, таким образом, в дни, когда никто из них не отдыхает, они срубают $A$ + $B$ деревьев, в дни, когда отдыхает только Федор — $A$ деревьев, а в дни, когда отдыхает только Дмитрий — $B$ деревьев. В дни, когда оба лесоруба отдыхают, ни одно дерево не срубается.

Фермер Николай хочет понять, за сколько дней лесорубы срубят все деревья, и он сможет засеять кукурузное поле.

Требуется написать программу, которая по заданным целым числам $A$, $K$, $B$, $M$ и $X$ определяет, за сколько дней все деревья в лесу будут вырублены.

Входные данные

Входной файл содержит пять целых чисел, разделенных пробелами: $A$, $K$, $B$, $M$ и $X$ (1 ≤ $A$, $B$ ≤ $10^9$ , 2 ≤ $K$, $M$ ≤ 10¹⁸, 1 ≤ $X$ ≤ 10¹⁸).

Выходные данные

Выходной файл должен содержать одно целое число — искомое количество дней.

Пояснения к примеру

В приведенном примере лесорубы вырубают 25 деревьев за 7 дней следующим образом:
* 1-й день: Дмитрий срубает 2 дерева, Федор срубает 3 дерева, итого 5 деревьев;
* 2-й день: Дмитрий срубает 2 дерева, Федор срубает 3 дерева, итого 10 деревьев;
* 3-й день: Дмитрий срубает 2 дерева, Федор отдыхает, итого 12 деревьев;
* 4-й день: Дмитрий отдыхает, Федор срубает 3 дерева, итого 15 деревьев;
* 5-й день: Дмитрий срубает 2 дерева, Федор срубает 3 дерева, итого 20 деревьев;
* 6-й день: Дмитрий срубает 2 дерева, Федор отдыхает, итого 22 дерева;
* 7-й день: Дмитрий срубает 2 дерева, Федор срубает оставшееся 1 дерево, итого все 25 деревьев срублены.
Внимание! Тест из примера не подходит под ограничения для подзадач 2 и 3, но решение принимается на проверку только в том случае, если оно выводит правильный ответ на тесте из примера. Решение должно выводить правильный ответ на тест даже, если оно рассчитано на решение только каких-либо из подзадач 2 и 3

Система оценки и описание подзадач

Подзадача 1 (32 балла)
1 ≤ $X$ ≤ 1000, 1 ≤ $A$, $B$ ≤ 1000, 2 ≤ $K$, $M$ ≤ 1000
Баллы за подзадачу начисляются только в случае, если все тесты успешно пройдены.
Подзадача 2 (10 баллов)
1 ≤ $X$ ≤ 10¹⁸
$X$ < $K$
$X$ < $M$
При решении этой подзадачи можно считать, что лесорубы не отдыхают.
Баллы за подзадачу начисляются только в случае, если все тесты успешно пройдены.
Подзадача 3 (10 баллов)
1 ≤ $X$ ≤ 10¹⁸
Дополнительно к приведенным ограничениям выполняется условие $K$ = $M$.
Баллы за подзадачу начисляются только в случае, если все тесты успешно пройдены.
Подзадача 4 (48 баллов)
1 ≤ $X$ ≤ 10¹⁸, 1 ≤ $A$, $B$ ≤ $10^9$, 2 ≤ $K$, $M$ ≤ 10¹⁸
В этой подзадаче 16 тестов, каждый тест оценивается в 3 балла. Баллы за каждый тест начисляются независимо.

Примеры

Входные данные

2 4 3 3 25

Выходные данные

Страница: << 6 7 8 9 10 11 12 >> Отображать по:

Выбрано

Отменить

Добавить в контест