Вы уже знаете, сколько нефти добывается в Ханты-Мансийском автономном округе. Другой хозяйственной отраслью Югры является оленеводство. Нередко можно увидеть, как на нефтяной площадке, окружённой изгородью, работают нефтяники, а вокруг изгороди пасутся олени.
Оленевод Ванхо привязал своего оленя Ахтамака к изгороди нефтяной площадки, имеющей форму выпуклого многоугольника. Олень был привязан на длинной верёвке, чтобы он не убежал и при этом мог пастись. Вокруг нефтяной вышки растёт такой вкусный ягель, что олень тут же принялся его щипать.
Напишите программу, вычисляющую площадь участка вне изгороди, ягель на котором будет доступен оленю. Форма изгороди, точка привязывания и длина верёвки задаются во входном файле.
В первой строке входного файла записано целое число \(n\) — количество углов изгороди (\(3\le n\le100\)). В последующих \(n\) строках записаны координаты углов изгороди в порядке обхода по часовой стрелке. В последней строке записаны три числа — координаты точки привязывания оленя к изгороди и длина верёвки. Все координаты целые и не превосходят по модулю \(10^4\). Длина верёвки — целое положительное число, не превосходящее \(10^4\). Числа в каждой строке разделены пробелами. Гарантируется, что изгородь представляет собой строго выпуклый многоугольник и точка привязывания оленя лежит на его границе.
В выходной файл выведите значение площади с точностью не менее \(10^{-3}\).
Система оценивания
Решения, корректно работающие на тестах из примеров, а также в случае, если длина верёвки не превосходит половины периметра изгороди и изгородь представляет собой прямоугольник со сторонами, параллельными осям координат, будут оцениваться из 30 баллов.
Решения, корректно работающие на тестах из примеров, а также в случае, если длина верёвки не превосходит половины периметра изгороди, будут оцениваться из 60 баллов.
4 -5 -5 -5 5 5 5 5 -5 5 0 4
25.1327412287
4 0 0 0 2 4 2 4 0 2 0 4
31.4159265359
Фермер Архип решил заняться земледелием и выращивать брюссельскую редиску. Для этого он купил прямоугольное поле, состоящее из \(n\) рядов по \(m\) участков в каждом. Все участки являются одинаковыми и имеют квадратную форму. Оказалось, что на момент покупки некоторые из этих участков уже удобрены, а некоторые — нет. Редиска растет только на удобренных участках.
Для получения большего урожая Архип решил удобрить некоторый прямоугольный фрагмент поля, состоящий из целых участков. В выбранном фрагменте Архип удобряет каждый участок. Повторное удобрение участка делает его непригодным к выращиванию брюссельской редиски. Закончив удобрять, фермер выбирает для посадки редиски прямоугольный фрагмент поля, состоящий из целых участков, каждый из которых удобрен ровно один раз.
Архип должен выбрать на поле фрагмент для удобрения таким образом, чтобы фрагмент для посадки редиски имел максимальную площадь.
Напишите программу, которая по заданному полю находит фрагмент поля для удобрения и фрагмент поля под посадку.
В первой строке входного файла записаны натуральные числа \(n\) и \(m\) (\(2\le n\le2\,000\), \(2\le m\le2\,000\)), где \(n\) — количество рядов на поле, а \(m\) — количество участков в каждом ряду (количество столбцов). Далее в \(n\) строках содержится описание поля. Каждая из этих \(n\) строк содержит \(m\) символов. Символ «1» обозначает, что соответствующий участок поля удобрен, а «0» — не удобрен. Гарантируется, что поле содержит хотя бы один удобренный и хотя бы один неудобренный участок. Поле расположено таким образом, что первая строка его описания соответствует северной стороне, а первый столбец — западной стороне.
Первая строка должна описывать фрагмент поля для удобрения. Фрагмент описывается четырьмя числами \(a\), \(b\), \(c\), \(d\), где \(a\) и \(b\) — номер ряда и столбца самого северо-западного его участка, а \(c\) и \(d\) — номер ряда и столбца самого юго-восточного. Ряды нумеруются с севера на юг от 1 до \(n\), а столбцы — с запада на восток от 1 до \(m\).
Вторая строка должна описывать фрагмент под посадку в том же формате.
Третья строка должна содержать площадь фрагмента (количество участков) под посадку.
Если решений несколько, выведите любое.
Система оценивания
Решения, корректно работающие при \(n\le40\) и \(m\le40\), будут оцениваться из 30 баллов, а решения, корректно работающие при \(n\le300\) и \(m\le300\), будут оцениваться из 60 баллов.
4 4 1110 1010 1110 0000
2 2 2 2 1 1 3 3 9
Юная программистка Агнесса недавно узнала на уроке информатики об арифметических выражениях. Она заинтересовалась вопросом, что случится, если из арифметического выражения удалить всё, кроме скобок. Введя запрос в своём любимом поисковике, она выяснила, что математики называют последовательности скобок, которые могли бы встречаться в некотором арифметическом выражении, правильными скобочными последовательностями.
Так, последовательность ()(()) является правильной скобочной последовательностью, потому что она может, например, встречаться в выражении (2+2) : (3–(5–2)+4), а последовательности (() и ())( не являются таковыми. Легко видеть, что существует пять правильных скобочных последовательностей, состоящих ровно из шести скобок (по три скобки каждого типа — открывающих и закрывающих): ((())), (()()), (())(), ()(()) и ()()().
Агнесса заинтересовалась простейшими преобразованиями правильных скобочных последовательностей. Для начала Агнесса решила ограничиться добавлением скобок в последовательность. Она очень быстро выяснила, что после добавления одной скобки последовательность перестаёт быть правильной, а вот добавление двух скобок иногда сохраняет свойство правильности. Например, при добавлении двух скобок в различные места последовательности ()() можно получить последовательности (()()), (())(), ()(()) и ()()(). Легко видеть, что при любом способе добавления двух скобок с сохранением свойства правильности одна из новых скобок должна быть открывающей, а другая — закрывающей.
Агнесса хочет подсчитать количество различных способов добавления двух скобок в заданную правильную скобочную последовательность так, чтобы снова получилась правильная скобочная последовательность. К сожалению, выяснилось, что это количество может быть в некоторых случаях очень большим. Агнесса различает способы получения последовательности по позициям добавленных скобок в полученной последовательности. Например, даже при добавлении скобок в простейшую последовательность () можно получить другую правильную скобочную последовательность семью способами: ()(), (()), (()), (()), (()), ()(), ()(). Здесь добавленные скобки выделены жирным шрифтом.
Таким образом, если в полученной последовательности добавленная открывающая скобка стоит в позиции \(i\), а добавленная закрывающая — в позиции \(j\), то два способа, соответствующие парам \((i_1, j_1)\) и \((i_2, j_2)\), считаются различными, если \(i_1\neq i_2\) или \(j_1\neq j_2\).
Требуется написать программу, которая по заданной правильной скобочной последовательности определяет количество различных описанных выше способов добавления двух скобок.
Входной файл состоит из одной непустой строки, содержащей ровно \(2n\) символов: \(n\) открывающих и \(n\) закрывающих круглых скобок. Гарантируется, что эта строка является правильной скобочной последовательностью.
Выведите в выходной файл количество различных способов добавления в заданную последовательность двух скобок таким образом, чтобы получилась другая правильная скобочная последовательность.
Данная задача содержит три подзадачи. Для оценки каждой подзадачи используется своя группа тестов. Баллы за подзадачу начисляются только в том случае, если все тесты из этой группы пройдены.
Величина \(n\) (количество скобок каждого типа) не превосходит 50.
Величина \(n\) (количество скобок каждого типа) не превосходит 2500.
Величина \(n\) (количество скобок каждого типа) не превосходит 50 000.
()
7
()()
17
(())
21
Для подготовки к чемпионату мира по футболу 2018 года создается школа олимпийского резерва. В нее нужно зачислить \(M\) юношей 1994−1996 годов рождения. По результатам тестирования каждому из \(N\) претендентов был выставлен определенный балл, характеризующий его мастерство. Все претенденты набрали различные баллы. В составе школы олимпийского резерва хотелось бы иметь \(A\) учащихся 1994 г.р., \(B\) – 1995 г.р. и \(C\) – 1996 г.р. (\(A + B + C = M\)). При этом минимальный балл зачисленного юноши 1994 г.р. должен быть больше, чем минимальный балл зачисленного 1995 г.р., а минимальный балл зачисленного 1995 г.р. должен быть больше, чем минимальный балл зачисленного 1996 г.р. Все претенденты, набравшие балл больше минимального балла для юношей своего года рождения, также должны быть зачислены.
В базе данных для каждого претендента записаны год его рождения и тестовый балл. Требуется определить, сколько нужно зачислить юношей каждого года рождения \(M_{94}\), \(M_{95}\) и \(M_{96}\) (\(M_{94} + M_{95} + M_{96} = M\)), чтобы значение величины \(F = |M_{94} − A| + |M_{95} − B| + |M_{96} − C|\) было минимально, все правила, касающиеся минимальных баллов зачисленных, были соблюдены, и должен быть зачислен хотя бы один юноша каждого требуемого года рождения.
В первой строке входного файла находится число \(K\) – количество наборов входных данных. Далее следуют описания каждого из наборов. В начале каждого набора расположены три натуральных числа \(A\), \(B\), \(C\). Во второй строке описания находится число \(N\) – количество претендентов (гарантируется, что \(N \geq A + B + C\)). В каждой из следующих \(N\) строк набора содержатся два натуральных числа – год рождения (число 1994, 1995 или 1996 соответственно) и тестовый балл очередного претендента.
Ответ на каждый тестовый набор выводится в отдельной строке. Если хотя бы одно из требований выполнить невозможно, то в качестве ответа следует вывести только число −1. В противном случае соответствующая строка сначала должна содержать минимальное значение величины \(F\), а затем три числа \(M_{94}\), \(M_{95}\) и \(M_{96}\), на которых это минимальное значение достигается, удовлетворяющие всем требованиям отбора. Если искомых вариантов несколько, то разрешается выводить любой из них.
В первом примере на первом наборе ответ не существует, потому что нельзя пригласить хотя бы одного юношу 1995 г.р. Во втором наборе ответ существует и единственный, в третьем – нельзя выполнить правило относительно минимальных баллов.
Во втором примере правильным является также ответ 2 2 2 2.
Данная задача содержит три подзадачи. Для оценки каждой подзадачи используется своя группа тестов. Баллы за подзадачу начисляются только в том случае, если все тесты из этой группы пройдены.
\(K = 1\); \(N \leq 100\); каждый претендент характеризуется своим баллом от 1 до \(N\).
Сумма значений \(N\) по всем тестовым наборам не превосходит 10 000, каждый претендент характеризуется своим баллом от 1 до \(10^9\).
Сумма значений \(N\) по всем тестовым наборам не превосходит 100 000, каждый претендент характеризуется своим баллом от 1 до \(N\).
Сумма значений \(N\) по всем тестовым наборам не превосходит 300 000, каждый претендент характеризуется своим баллом в диапазоне от 1 до \(10^9\).
3 1 1 1 4 1994 3 1994 4 1996 1 1996 2 1 1 1 3 1995 2 1994 3 1996 1 1 1 1 3 1994 1 1995 2 1996 3
-1 0 1 1 1 -1
1 2 3 1 7 1996 2 1994 7 1994 4 1996 1 1995 3 1994 5 1995 6
2 3 2 1
К 50-летию первого пилотируемого полета в космос решено создать новый тип космического корабля многоразового использования “Восторг”. Прямоугольная часть его корпуса (далее прямоугольник) должна быть облицована квадратными термозащитными плитками разных цветов одного и того же размера. Прямоугольник состоит из \(r\) рядов по \(c\) плиток в каждом. Плитки должны образовывать заданный рисунок.
Облицовка космического корабля отдельными плитками очень трудоемка, поэтому для выкладывания заданного рисунка используются одинаковые прямоугольные панели, состоящие из плиток. Панели крепятся на корпусе одна за другой, заполняя ряд за рядом сверху вниз. Каждый ряд панелей может быть сдвинут относительно предыдущего на одно и то же число плиток. При этом панели могут выходить за пределы прямоугольника. Панели должны быть одинаково ориентированы, то есть при параллельном переносе одной панели на место другой цвета образующих эти панели плиток должны совпадать.
Главный конструктор хочет выбрать такой размер панели \(a\times b\) и сдвиг \(s\), чтобы этими панелями можно было выложить заданный рисунок, и площадь панели была минимальна.
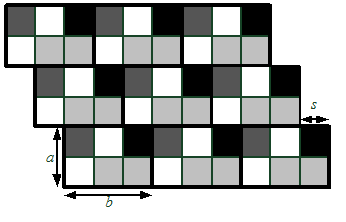
Пример панелей с \(a = 2\), \(b = 3\), \(s = 1\).
Требуется написать программу, которая по заданному расположению плиток в прямоугольнике рассчитывает размеры минимальной по площади панели, которую можно использовать при его облицовке, а также величину сдвига вправо (\(0 \leq s < b\)) каждого следующего ряда относительно предыдущего.
Первая строка входного файла содержит два целых числа: \(r\) и \(c\) – размеры прямоугольника в плитках. В последующих \(r\) строках указаны цвета плиток фрагмента. Каждый из \(k \leq 26\) цветов обозначен одной из первых \(k\) прописных букв латинского алфавита. Гарантируется, что для этого прямоугольника можно подобрать панель размера \(a\times b\), такую, что \(2a \leq r\) и \(2b \leq c\).
ВВ выходной файл необходимо вывести три целых числа \(a\), \(b\) и \(s\), удовлетворяющих условиям задачи. Если решений несколько, разрешается вывести любое из них.
Во втором примере облицовка прямоугольника соответствуют следующему рисунку (выступающие за границы прямоугольника части панелей не показаны):

Данная задача содержит семь подзадач. Для оценки каждой подзадачи используется своя группа тестов. Баллы за подзадачу начисляются только в том случае, если все тесты из этой группы пройдены.
В правильном ответе величина сдвига \(s\) равна нулю, \(r\) и \(c\) не превосходят 20.
В правильном ответе величина сдвига \(s\) равна нулю, \(r\) и \(c\) не превосходят 200.
В правильном ответе величина сдвига \(s\) равна нулю, \(r\) и \(c\) не превосходят 1961.
Величина сдвига \(s\) произвольна, \(r\) и \(c\) не превосходят 20.
Величина сдвига \(s\) произвольна, \(r\) и \(c\) не превосходят 200.
Величина сдвига \(s\) произвольна, \(r\) и \(c\) не превосходят 500.
Величина сдвига \(s\) произвольна, \(r\) и \(c\) не превосходят 1961.
2 4 ABAB ABAB
1 2 0
5 7 DCADCAD BABBABB ADCADCA BBABBAB CADCADC
2 3 1