На плоскости задано такое множество из N многоугольников, что выполняются следующие условия:
Напишите программу, которая для каждого многоугольника выдает количество многоугольников, внутри которых он находится.
Первая строка входного файла содержит целое число N — количество многоугольников, 3≤N≤100000. Следующие N строк файла описывают N многоугольников. (i+1)–ая строка файла описывает i–ый многоугольник. Первое целое число Ci — количество вершин многоугольника, 3≤Ci≤20. Последующие Ci пар чисел — координаты вершин многоугольника в порядке его обхода. Координаты вершин — целые числа, принадлежащие диапазону от -2 000 000 000 до 2 000 000 000.
Единственная строка выходного файла должна содержать N чисел: i–ое число строки должно быть Pi — количество многоугольников, внутри которых находится i–ый многоугольник.
3 3 -2 1 8 9 12 1 3 7 5 6 3 7 4 4 4 3 7 7 9 3 1 2
0 2 1
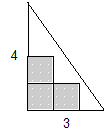Территория Великой Треугольной Области (ВТО) представляет собой прямоугольный треугольник. Длины его катетов равны M и N государственных единиц длины (ГЕД). Правительство ВТО решило покрыть как можно большую часть территории области квадратными плитами размером 11 ГЕД. Плиты должны плотно прилегать друг к другу и к катетам ВТО. Разрезать плиты нельзя.
Согласно межгосударственным соглашениям, правительство ВТО не имеет права покрыть частью своей плиты чужую территорию. Производитель поставляет плиты только контейнерными партиями — по P плит. Правительство заказывает столько контейнеров, сколько необходимо для реализации проекта.
Заведующий центральным складом, узнав про проект, решил, что его интересует количество плит, которые останутся на складе из последнего контейнера после покрытия территории ВТО.
Напишите программу, которая по длинам катетов ВТО и вместимости контейнера находит количество плит, которые останутся на складе после осуществления проекта.
Единственная строка входного файла содержит три целых числа: M, N (2≤M, N≤2 000 000 000) и P (100≤P≤10 000).
Единственная строка выходного файла должна содержать целое число — количество неиспользованных плит из последнего контейнера.
4 3 100
97
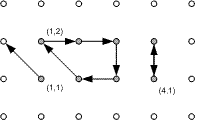На плоскости задано множество точек (x, y), где x, y – целые числа, 1≤x≤M, 1≤y≤N. Из каждой точки выходит ровно один из следующих векторов: (-1,-1), (-1,0), (-1,1), (0,1), (1,1), (1,0), (1,-1), (0,-1). Каждый вектор соединяет одну целочисленную точку плоскости с другой. Например, если из точке (2, 5) выходит вектор (1, 1), то он соединяет эту точку с (3, 6), но не наоборот.
Последовательность из двух и более точек плоскости a1, a2,…, ak назовем циклом, если каждая точка ai соединена вектором с ai+1 (1≤i≤k-1), и ak соединена вектором с a1. Циклы считаются разными если они отличаются хотя бы одной вершиной.
Напишите программу, которая по информации о векторах, выходящих из точек плоскости, находит количество различных циклов.
Первая строка входного файла содержит два целых числа N (1≤N≤100) и M (1≤M≤100). Каждая из последующих N строк, содержит M пар чисел (т.е. 2≤M чисел). Пара x, которая находится в строке y, задает вектор в точке (x, y).
Единственная строка выходного файла должна содержать целое число – количество циклов, образованных векторами.
2 4 -1 1 -1 1 -1 0 0 1 1 0 1 0 0 -1 0 -1
2
На заводе каждая из N деталей может быть обработанной на одном из двух станков: A или B. Каждая деталь имеет порядковый номер от 1 до N. К обработке детали поступают последовательно, в соответствии со своими номерами. Количество деталей всегда четно.
Существуют правила, по которым определяется можно ли обрабатывать деталь на определенном станке.
Сколько людей, столько и мнений. Каждый из работников этого завода предложил свою последовательность обработки деталей, причем все предложения оказались разными, но удовлетворяющими правилам 1 и 2.
Напишите программу, которая по информации о количестве деталей N определяет максимально возможное количество работников завода.
Единственная строка входного файла содержит четное число N (2≤N≤28) – количество деталей которое необходимо обработать.
Единственная строка выходного файла должна содержать целое число – максимально возможное количество работников завода.
Первый работник считает, что на станке A необходимо обработать детали 1 и 2, а на станке B, соответственно, 3 и 4. Второй думает, что на станке A нужно обработать детали 1 и 3, а на станке B – детали 2 и 4. Других вариантов последовательности обработки не существует.
4
2
Робот движется по полю, которое состоит из N клеток, выстроенных в ряд. На каждой из клеток находится кубик определенного цвета.
До начала движения робот находится на первой клетке поля и не держит ни одного кубика. Находясь на клетке, робот может выполнить не более одного раза каждую из следующих операций: (1) положить кубик того же цвета, который лежит на текущей клетке; (2) поднять с клетки тот кубик, который находился там сначала. После этого робот перемещается на следующую клетку или останавливается, если текущая клетка последняя в поле.
Одновременно робот может держать не более K кубиков. На момент остановки робот не должен держать ни одного кубика.
Напишите программу, которая по информации о цвете кубиков и ограничении на количество кубиков, которое может держать робот, определяет максимальное общее количество кубиков, которое робот может перенести с места на место, двигаясь по полю.
Первая строка входного файла содержит символьную строку длинны N (1≤N≤1000). Строка состоит из маленьких букв латинского алфавита. Каждая буква соответствует клетке поля и определяет цвет кубика, который находится в этой клетке. Вторая строка содержит ограничение на количество кубиков, которое одновременно может держать робот K (1≤K≤25).
Единственная строка выходного файла должна содержать целое число — максимальное количество кубиков, месторасположение которых робот может изменить, двигаясь по полю.
Подзадачи и система оценки
Баллы за эту задачу будут начислены если ваше решение проходит все тесты
rgbbggrmcm 2
4