#112573

Data Packing

Темы: [Алгоритмы сортировки]

Источники: [ Личные олимпиады, Интернет-олимпиады, Google Code Jam, Data Packing ]

Адам, будучи организованным человеком, всегда любит порядок. Иногда он любит вспоминать, как когда-то проводил долгие часы за компьютером, перенося данные на диски.

Есть два важных правила хранения данных на дисках: Адам никогда не хранит более двух файлов на одном диске (это нужно, чтоб ему было проще их подписывать), он никогда не делит файл на части. Но диски достаточно большие, чтобы уместить любой файл.

Адам использует диски одного размера. Помогите ему разместить файлы, в соответствии с правилами, используя минимальное количество дисков.

1 ≤ T ≤ 100. 1 ≤ X ≤ 700. 1 ≤ S _i ≤ X .

В задаче есть две группы тестов: 1. 1 ≤ N ≤ 10 - оценивается в 40 баллов 2. 1 ≤ N ≤ 1 ⁴ - оценивается в 60 баллов

Входные данные

Первая строка входного файла содержит число N - количество файлов и X - ёмкость одного диска. Во второй строке дано N чисел S _i - размеры файлов.

Выходные данные

Выведите одно число - минимальное количество дисков, умещающих все файлы по правилам.

Примеры

Входные данные

3 100
10 20 70

Выходные данные

Входные данные

4 100
30 40 60 70

Выходные данные

Входные данные

5 100
10 20 30 40 60

Выходные данные

#112589

Министерство

Темы: [Алгоритмы на графах] [Хеш]

Источники: [ Личные олимпиады, Central European Olympiad in Informatics , Central European Olympiad in Informatics 2007, Министерство ]

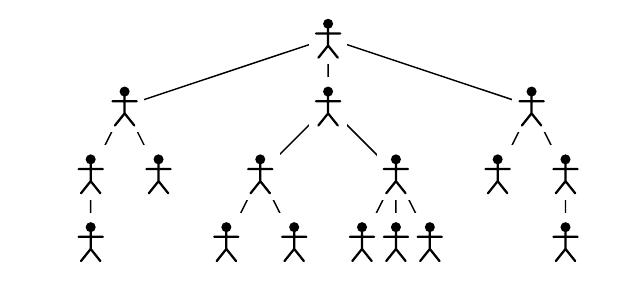
Однажды в далекой-далекой стране правительство создало Министерство по сокращению бумажной волокиты. Как вы наверное догадались, это было крупнейшее министерство за всю историю страны. Количество сотрудников было поистине огромным. Несмотря на это, структура министерства была очень простой: каждый сотрудник имел не более трёх подчинённых, каждый из которых снова имел не более трех подчиненных и так далее...

В результате последних выборов был избран новый министр. Он был молод, умён и непорочен, и сразу же решил оправдать название своего учреждения. Он заметил, что многие части иерархической структуры совпадают, и решил, что должны совпадать и их обязанности. А если две структуры делают одно и тоже, одна из них является лишней, и ее работники должны быть уволены. Ваша задача найти количество различных департаментов и вывести результат в необходимом формате.

Вам дана структура министерства. Каждый работник имеет одного начальника и не более трёх подчинённых(возможно ноль). Единственным исключением является министр — у него нет начальника(но так же не более трех подчинённых). Конечно нет определённого порядка, в котором перечисляются подчинённые. Департамент состоит из должностного лица, всех его подчинённых и их подчинённых, и т.д.

Есть два особых случая:

Департамент, в котором должностное лицо — сам министр, тогда этот департамент есть всё министерство.
Департамент, в котором у должностного лица нет ни одного подчинённого.

Высотой департамента назовем длину максимальной последовательность сотрудников x ₁ , ..., x _d такую, что сотрудник x _i является начальником сотрудника x _{i

+ 1} для всех 1 ≤ i < d . Заметим что высота департамента, состоящего из одного сотрудника равна 1 .

Два департамента A и B совпадают, если существует взаимно-однозначное отображение, сопоставляющее каждому сотруднику x _A из департамента A сотрудника x _B из департамента B , таким образом, что сотрудник x _A является начальником сотрудником y _A , тогда и только тогда, когда x _B является начальником y _B . Заметим, что если два департамента совпадают, то они имеют одинаковую высоту, одинаковое количество сотрудников и начальнику первого департамента соответствует начальник второго.

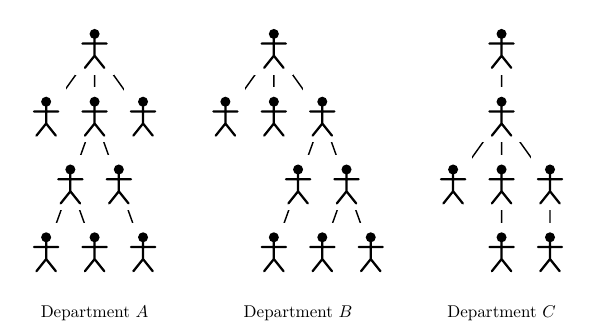
На приведенных картинках департаменты A и B совпадают, а C не совпадает ни с A , ни c B .

$\text{[math]}$

Вам необходимо для каждой высоты вычислить количество различных департаментов имеющих такую глубину. Формально требуется построить последовательность n ₁ , ..., n _d , где d это высота всего министерства, а n _i — количество различных департаментов высоты i .

Входные данные

Входной файл содержит единственную строку, которая описывает иерархическую структуру министерства, используя следующую нотацию. Каждый департамент кодируются строкой "( x ₁ ... x _k )", где k — количество подчинённых у начальника департамента, а строки x _i — коды им подчиняющихся департаментов. Департамент, состоящий из одного человека, кодируется строкой "()". Структура министерства задается кодом всего министерства. Количество сотрудников министерства не превосходит 1 000 000 (включая министра).

Выходные данные

Выходной файл должен содержать d строк, где d это высота министерства. i -ая строка должна содержать количество различных департаментов высоты i .

Примечание

Приведенная картинка иллюстрирует пример из условия. $\text{[math]}$

Примеры

Входные данные

(((())())((()())(()()()))(()(())))

Выходные данные

#112744

Выбор зала

Темы: [Формула]

Источники: [ Личные олимпиады, Всероссийская олимпиада школьников, Региональный этап, 2015, 1 день, Выбор зала ] [ Личные олимпиады, Всероссийская олимпиада школьников, Региональный этап, 2015, 1 день, Задача A ]

Для проведения церемонии открытия олимпиады по информатике организаторы осуществляют поиск подходящего зала. Зал должен иметь форму прямоугольника, длина каждой из сторон которого является целым положительным числом. Чтобы все участники церемонии поместились в зале, и при этом он не выглядел слишком пустым, площадь зала должна находиться в пределах от $A$ до $B$ квадратных метров, включительно.

Чтобы разместить на стенах зала плакаты, рассказывающие об успехах школьников на олимпиадах, но при этом не создать ощущения, что успехов слишком мало, периметр зала должен находиться в пределах от $C$ до $D$ метров, включительно. Прежде чем сделать окончательный выбор, организаторы олимпиады решили просмотреть по одному залу каждого подходящего размера. Залы с размерами $Y$ × $Z$ и $Z$ × $Y$ считаются одинаковыми. Чтобы понять необходимый объем работ по просмотру залов организаторы задались вопросом, сколько различных залов удовлетворяют приведенным выше ограничениям. Требуется написать программу, которая по заданным $A$, $B$, $C$ и $D$ определяет количество различных залов, площадь которых находится в пределах от $A$ до $B$, а периметр — от $C$ до $D$, включительно.

Входные данные

Входной файл содержит четыре разделенных пробелами целых числа: $A$, $B$, $C$ и $D$ (1 ≤ $A$ ≤ $B$ ≤ $10^9$ , 4 ≤ $C$ ≤ $D$ ≤ $10^9$ )

Выходные данные

Выходной файл должен содержать одно число — искомое количество залов.

Пояснения к примеру

В примере ограничениям удовлетворяют залы следующих размеров: 1 × 2, 1 × 3, 2 × 2

Система оценки и описание подзадач

Подзадача 1 (50 баллов)
1 ≤ $A$ ≤ $B$ ≤ 1000, 4 ≤ $C$ ≤ $D$ ≤ 1000.
Баллы за подзадачу начисляются только в случае, если все тесты успешно пройдены.
Подзадача 2 (50 баллов)
1 ≤ $A$ ≤ $B$ ≤ $10^9$,
4 ≤ $C$ ≤ $D$ ≤ $10^9$.
Баллы за подзадачу начисляются только в случае, если все тесты успешно пройдены.

Примеры

Входные данные

2 10 4 8

Выходные данные

#112745

Призы(2015)

Источники: [ Личные олимпиады, Всероссийская олимпиада школьников, Региональный этап, 2015, 1 день, Задача B ]

Алиса и Боб стали победителями телевикторины, и теперь им предстоит выбрать себе призы. На выбор предлагается n призов, пронумерованных от 1 до $n$.

Распределение призов происходит следующим образом. Организаторы телевикторины сообщают победителям целое положительное число $k$ (1 ≤ $k$ ≤ $n$ / 3). Сначала Алиса выбирает себе любые $k$ подряд идущих номеров призов. Потом Боб выбирает себе k подряд идущих номеров призов, при этом он не может выбирать номера, которые уже выбрала Алиса. После этого победители забирают выбранные ими призы.

Алиса хорошо знает Боба, и для каждого приза выяснила его ценность для Боба, которая является целым положительным числом. Алиса обижена на Боба и хочет выбрать свои призы так, чтобы суммарная ценность призов, которые достанутся Бобу, была как можно меньше. При этом Алису не волнует, какие призы достанутся ей.

Требуется написать программу, которая по информации о ценности призов и значению $k$ определит, для какого минимального значения x Алиса сможет добиться того, чтобы Боб не смог выбрать призы с суммарной ценностью больше $x$

Входные данные

Первая строка входного файла содержит два целых числа: $n$ — общее количество призов и $k$ — количество подряд идущих номеров призов, которое должен выбрать каждый из победителей (3 ≤ $n$ ≤ 100 000, 1 ≤ $k$ ≤ $n$ / 3).

Вторая строка содержит $n$ целых положительных чисел: $a_1$, $a_2$, …, $a_n$. Для каждого приза указана его ценность для Боба (1 ≤ $a_i$ ≤ $10^9$)

Выходные данные

Выходной файл должен содержать одно число — минимальное значение $x$, для которого Алиса сможет добиться того, чтобы Боб не смог выбрать призы с суммарной ценностью больше $x$

Пояснения к примеру

В приведенном примере Алиса может, например, выбрать 4-й и 5-й призы. После этого для Боба оптимально выбрать 9-й и 10-й призы с суммарной ценностью 7.

Система оценки и описание подзадач

В этой задаче три подзадачи. Баллы за подзадачу начисляются только в случае, если все тесты для данной подзадачи успешно пройдены.

Подзадача 1 (30 баллов)
3 ≤ $n$ ≤ 50, 1 ≤ $a_i$ ≤ $10^5$
Подзадача 2 (30 баллов)
3 ≤ $n$ ≤ 5000, 1 ≤ $a_i$ ≤ $10^5$
Подзадача 3 (40 баллов)
3 ≤ $n$ ≤ 100 000, 1 ≤ $a_i$ ≤ $10^9$

Примеры

Входные данные

10 2
1 2 4 5 2 4 2 2 1 6

Выходные данные

#112746

Река

Источники: [ Личные олимпиады, Всероссийская олимпиада школьников, Региональный этап, 2015, 1 день, Задача C ]

Во Флатландии протекает богатая рыбой река Большой Флат. Много лет назад река была поделена между $n$ рыболовными предприятиями, каждое из которых получило непрерывный отрезок реки. При этом $i$-е предприятие, если рассматривать их по порядку, начиная от истока, изначально получило отрезок реки длиной $a_i$ .

С тех пор с рыболовными предприятиями во Флатландии k раз происходили различные события. Каждое из событий было одного из двух типов: банкротство некоторого предприятия или разделение некоторого предприятия на два.

При некоторых событиях отрезок реки, принадлежащий предприятию, с которым это событие происходит, делится на две части. Каждый такой отрезок имеет длину большую или равную 2. Деление происходит по следующему правилу. Если отрезок имеет четную длину, то он делится на две равные части. Иначе он делится на две части, длины которых различаются ровно на единицу, при этом часть, которая ближе к истоку реки, имеет меньшую длину.

При банкротстве предприятия происходит следующее. Отрезок реки, принадлежавший обанкротившемуся предприятию, переходит к его соседям. Если у обанкротившегося предприятия один сосед, то этому соседу целиком передается отрезок реки обанкротившегося предприятия. Если же соседей двое, то отрезок реки делится на две части описанным выше способом, после чего каждый из соседей присоединяет к своему отрезку ближайшую к нему часть.

При разделении предприятия отрезок реки, принадлежавший разделяемому предприятию, всегда делится на две части описанным выше способом. Разделившееся предприятие ликвидируется, и образуются два новых предприятия. Таким образом, после каждого события каждое предприятие владеет некоторым отрезком реки.

Министерство финансов Флатландии предлагает ввести налог на рыболовные предприятия, пропорциональный квадрату длины отрезка реки, принадлежащего соответствующему предприятию. Чтобы проанализировать, как будет работать этот налог, министр хочет по имеющимся данным узнать, как изменялась величина, равная сумме квадратов длин отрезков реки, принадлежащих предприятиям, после каждого произошедшего события.

Требуется написать программу, которая по заданному начальному разделению реки между предприятиями и списку событий, происходивших с предприятиями, определит, чему равна сумма квадратов длин отрезков реки, принадлежащих предприятиям, в начальный момент времени и после каждого события.

Входные данные

Первая строка входного файла содержит два целых числа: $n$ и $p$ — исходное количество предприятий (2 ≤ $n$ ≤ 100 000) и номер подзадачи (0 ≤ $p$ ≤ 4).

Вторая строка входного файла содержит $n$ целых чисел $a_1$, $a_2$, …, $a_n$ — длины исходных отрезков реки.

Третья строка входного файла содержит целое число $k$ — количество событий, происходивших с предприятиями (1 ≤ $k$ ≤ 100 000).

Последующие $k$ строк содержат описания событий, $i$-я строка содержит два целых числа: $e_i$ и $v_i$ — тип события и номер предприятия, с которым оно произошло. Значение $e_i$ = 1 означает, что предприятие, которое после всех предыдущих событий является $v_i$-м по порядку, если считать с единицы от истока реки, обанкротилось, а значение $e_i$ = 2 означает, что это предприятие разделилось на два.

Гарантируется, что значение $v_i$ не превышает текущее количество предприятий. Гарантируется, что если отрезок предприятия при банкротстве или разделении требуется поделить на две части, то он имеет длину большую или равную 2. Гарантируется, что если на реке осталось единственное предприятие, оно не банкротится.

Выходные данные

Выходной файл должен содержать ($k$ + 1) целых чисел, по одному в строке. Первая строка должна содержать исходную сумму квадратов длин отрезков реки, а каждая из последующих $k$ строк — сумму квадратов длин отрезков реки после очередного события.

Пояснения к примеру

Система оценки и описание подзадач

В этой задаче четыре подзадачи. Баллы за каждую подзадачу начисляются только в случае, если все тесты для данной подзадачи успешно пройдены.

Внимание! Тест из примера не подходит под ограничение подзадачи 3. Тем не менее, решение задачи принимается на проверку только в том случае, если оно выводит правильный ответ на тесте из примера, даже если участник претендует на правильное решение только этой подзадачи.

В первой строке каждого теста после числа n указан номер подзадачи, для теста из примера указано число 0, в тестах первой подзадачи указано число 1, и т. д.

Подзадача 1 (30 баллов)
2 ≤ $n$ ≤ 100, 1 ≤ $k$ ≤ 100, 1 ≤ $a_i$ ≤ 100, $p$ = 1
Подзадача 2 (30 баллов)
2 ≤ $n$ ≤ 100 000, 1 ≤ $k$ ≤ 100 000, 1 ≤ $a_i$ ≤ $10^4$, $p$ = 2
Для всех $i$ от 1 до $k$ – 1 выполнено условие: |$v_i$ – $v_{i + 1}$| ≤ 10
Подзадача 3 (20 баллов)
2 ≤ $n$ ≤ 100 000, 1 ≤ $k$ ≤ 100 000, 1 ≤ $a_i$ ≤ $10^4$, $p$ = 3
Все события имеют тип $e_i$ = 1 (нет разделений предприятий, только банкротства).
Подзадача 4 (20 баллов)
2 ≤ $n$ ≤ 100 000, 1 ≤ $k$ ≤ 100 000, 1 ≤ $a_i$ ≤ $10^4$, $p$ = 4

Примеры

Входные данные

Выходные данные

Страница: << 141 142 143 144 145 146 147 >> Отображать по: