Страница: << 42 43 44 45 46 47 48 >> Отображать по:
#1254
Монотонная последовательность
  
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
64 megabytes

Вася с Петей играют в следующую игру. Вася берет n картонных карточек, и на каждой из них с обеих сторон пишет по числу. После этого он выкладывает карточки в некотором порядке перед Петей. Пронумеруем карточки от 1 до n в том порядке, в котором их выложил Вася.

Петя пытается добиться того, чтобы последовательность чисел, написанных на карточках стала строго монотонной (возрастающей или убывающей). Для этого ему разрешается совершать следующие действия: выбрать два числа l и r, такие что 1 ≤ l≤ r ≤ n и перевернуть каждую из карточек от карточки номер l до карточки номер r.

Напомним, что последовательность c1, . . . , cn называется строго возрастающей, если выполняются неравенства c1 < c2 < … < cn, и строго убывающей, если выполняются неравенства c1 > c2 > … > cn.

Напишите программу, которая по описанию карточек определяет, какое минимальное число действий должен совершить Петя для того, чтобы добиться своей цели.

Входные данные

Первая строка входного файла содержит целое число n (1 ≤ n ≤ 100000). Каждая из последующих n строк описывает одну карточку и содержит два числа — ai написано на ее лицевой стороне, а bi — на оборотной. Все числа ai и bi находятся в диапазоне от 1 до 109.

Выходные данные

В первой строке выходного файла выведите минимальное число действий, которое должен совершить Петя. Если Петина цель недостижима, то выведите в выходной файл число -1.

Комментарий к примеру тестов

В первом примере для достижения цели Петя может перевернуть карточки со второй по третью.

В третьем примере можно, например, первым действием перевернуть карточки со второй по шестую, а вторым — четвертую карточку.

Примеры
Входные данные
3
3 4
1 2
4 1
Выходные данные
1
Входные данные
3
1 2
4 1
3 4
Выходные данные
-1
Входные данные
6
1 2
3 2
2 3
4 5
6 5
5 6
Выходные данные
2
#1255
Плакат
  
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
64 megabytes

Министерство образования Флатландии недавно приняло решение о начале реализации проекта по использованию социальной рекламы для повышения грамотности населения. Социальная реклама будет размещаться в виде видеороликов на телевидении, плакатов на улицах городов, а также в журналах и газетах.

Один из плакатов, подготовленных в рамках этого проекта, выполнен в весьма абстрактном стиле. Плакат имеет форму прямоугольника высотой h и шириной w, который изначально полностью покрашен в белый цвет. На плакате изображены несколько прямоугольников разных цветов.

Для того, чтобы напечатать этот плакат службе снабжения министерства образования необходимо выяснить, сколько краски какого цвета для этого требуется.

Так как во Флатландии повсеместно внедрены информационные технологии, то подготовка плаката велась с помощью специальной программы. В этой программе (как и во многих других) цвета представляются в так называемом RGB-формате. Это означает, что цвет кодируется тремя целыми числами, каждое из которых находится в пределах от 0 до 31 (обычно используются значения от 0 до 255, но оборудование, используемое для печати, обладает ограниченными возможностями цветопередачи). Эти числа обозначают интенсивность красной, зеленой и синей компонент цвета (0 соответствует отсутствию соответствующей компоненты, а 31 — ее максимальной интенсивности).

Таким образом, черный цвет кодируется как (0; 0; 0), а белый — как (31; 31; 31).

Цвета различных областей плаката определяются следующим образом. Изначально весь плакат заполняется белым цветом (таким образом, исходно все точки имеют цвет (31; 31; 31)), после чего выполняется рисование прямоугольников, заданных в описании плаката. При рисовании прямоугольника цветом, который кодируется как (r; g; b), новые цвета точек, находящихся внутри этого прямоугольника, определяются так: если до рисования точка имела цвет (r1; g1; b1), то после того, как прямоугольник будет нарисован, ее цвет будет равен ((r1+r) mod 32; (g1+g) mod 32; (b1+b) mod 32).

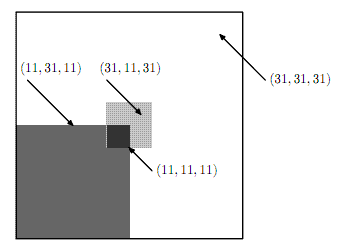
Например, на рисунке приведен плакат, который получается из белого листа размера 10 # 10 изображением двух прямоугольников: цвета (12; 0; 12) с координатами левого нижнего угла (0; 0) и правого верхнего (5; 5), а затем цвета (0; 12; 0) с координатами левого нижнего угла (4; 4) и правого верхнего (6; 6).


Таким образом, цвет каждой точки зависит от того, в каких прямоугольниках она лежит, и от того, каковы их цвета. Ваша задача состоит в том, чтобы написать программу, которая по описанию плаката вычислит число различных цветов, которые на нем присутствуют, а также площадь, закрашенную каждым из этих цветов.

Входные данные

Первая строка входного файла содержит число n прямоугольников, изображенных на плакате (0 ≤ n ≤ 1500). Вторая строка входного файла содержит два целых числа w и h — соответственно, ширину и высоту плаката (1 ≤ w, h ≤ 109). Каждая из последующих n строк описывает один из прямоугольников, изображенных на плакате, и содержит семь целых чисел: x1, y1, x2, y2, r, g, b. Первые два из них — координаты левого нижнего угла прямоугольника, третье и четвертое — координаты правого верхнего угла. Для этих чисел выполняются неравенства 0 ≤ x1 < x2 ≤ w, 0 ≤ y1 < y2 ≤ h. Пятое, шестое и седьмое числа задают цвет прямоугольника — они равны, соответственно, красной, зеленой и синей компонентам цвета (0 ≤ r, g, b ≤ 31).

Система координат введена таким образом, что левый нижний угол плаката имеет координаты (0; 0), а правый верхний — (w, h).

Выходные данные

В первой строке выходного файла выведите число k различных цветов, которые необходимы для печати плаката. Далее выведите k строк — каждая из них должна содержать четыре числа — первые три из них должны описывать цвет (первое из них должно быть равно значению красной компоненты, второй — зеленой, а третье — синей), а четвертое должно быть равно площади части плаката, которая будет закрашена этим цветом.

Примеры
Входные данные
2
10 10
0 0 5 5 12 0 12
4 4 6 6 0 12 0
Выходные данные
4
11 11 11 1
11 31 11 24
31 11 31 3
31 31 31 72
Входные данные
0
7 8
Выходные данные
1
31 31 31 56
Входные данные
2
10 10
0 0 5 5 20 21 22
4 4 6 6 15 16 17
Выходные данные
4
2 4 6 1
14 15 16 3
19 20 21 24
31 31 31 72
#1277
Несчастливые номера
  

Обычно автобусный билет с номером, состоящим из 6 цифр, считается счастливым, если сумма первых трех цифр его номера была равна сумме трех последних. Школьник Вася очень любил получать счастливые билеты, однако это случалось не так часто. Поэтому для себя он изменил определение счастливого билета. Счастливым он считал тот номер, сумма некоторых цифр которого равнялась сумме оставшихся цифр. В его представлении билет с номером 561743 счастливый, так как 5 + 1 + 4 + 3 = 6 + 7.

Вася вырос, но по привычке в номерах различных документов пытается найти признаки счастливого номера ☺. Для этого он расширил свое определение счастливого номера на n-значные номера лицевых счетов и других документов, состоящих из цифр от 0 до k (1 ≤ k ≤ 9). Номер документа он называет счастливым, если сумма некоторых цифр этого номера равняется сумме оставшихся. Остальные номера для него несчастливые. К сожалению, несмотря на расширенное понимание “счастья”, несчастливых номеров остается еще много...

Вам предлагается определить количество несчастливых n-значных номеров, которые можно составить, используя цифры от 0 до k. В номерах допускается любое количество ведущих нулей.

Входной файл unlucky.in содержит описание нескольких видов номеров. Каждый вид номеров определяется значениями n и k. Для данного входного файла вы должны создать соответствующий ему выходной файл и отправить его на проверку жюри.

Входные данные

Входной файл содержит несколько пар значений n и k, каждая пара записана в отдельной строке.

Выходные данные

Для каждой пары значений n и k входного файла выведите в соответствующей строке выходного файла искомое количество несчастливых билетов или 0, если такое число вам получить не удалось. Количество строк во входном и выходном файлах должно совпадать.

Примечание

За правильное решение задачи для каждого вида номеров вы получите 5 баллов. Так, представленный в примере выходной файл соответствует 15 баллам.

При сдаче на проверку выходного файла во время тура вы будете получать одно из двух сообщений:

  • Presentation Error — если файл не соответствует формату вывода. В этом случае файл не принимается на проверку.
  • Accepted — если файл формату вывода соответствует. В этом случае файл принимается на проверку. Проверка правильности ответов в выходном файле осуществляется только после окончания тура.
Содержание файла unlucky.in:
4 1
7 1
3 2
6 2
22 2
7 9
8 7
9 6
8 8
12 9
20 9
20 3
17 5
16 7
15 9
19 5
26 9
100 3
99 4
50 5
#1281
Счастливые цифры
  
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
64 megabytes

Школьнику Васе нравятся числа, которые заканчиваются счастливыми для него цифрами k. Поэтому каждый раз, когда он видит какое-нибудь натуральное число n, он сразу пытается подобрать такое d (d ≥ 2), что число n в системе счисления с основанием d заканчивается как можно большим количеством цифр k.

Требуется написать программу, которая по заданным числам n и k найдет такое d, чтобы число n в системе счисления с основанием d заканчивалось как можно большим количеством цифр k.

Входные данные

Вводятся  два целых десятичных числа n и k (1 ≤ n ≤ 1011; 0 ≤ k ≤ 9).

Выходные данные

Выведите два числа: d — искомое основание системы счисления и l — количество цифр k, которым заканчивается запись числа n в этой системе счисления. Если искомых d несколько, выведите любое из них, не превосходящее 1012 (такое всегда существует).

Примеры

 

 

комментарий

49 1

3 2

4910 = 12113

7 5

3 0

Ни в одной системе счисления 7 не заканчивается на цифру 5
Примеры
Входные данные
4 4
Выходные данные
5 1
Входные данные
9 9
Выходные данные
10 1
#1282
Тапкодёр
  
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes

Ассоциация Тапкодер организует Всемирное парное соревнование сильнейших программистов. К участию в соревновании допущены первые 2k зарегистрировавшихся участников, которым присвоены номера от 1 до 2k.

Соревнование будет проходить по олимпийской системе. В первом туре первый участник встречается со вторым, третий с четвертым и так далее. В каждой паре победителем становится участник, первым решивший предложенную задачу, при этом ничьих не бывает. Все победители очередного тура и только они являются участниками следующего тура. В каждом туре пары составляются из участников в порядке возрастания присвоенных им номеров. Соревнование продолжается до тех пор, пока не останется один победитель.

Организаторам стало известно, что некоторые пары участников заранее договорились о результате встречи между собой, если такая встреча состоится. Для всех остальных встреч, кроме n договорных, возможен любой исход.

Некоторые m участников соревнования представили свои резюме в ассоциацию Тапкодер с целью поступления на работу. Организаторов интересует, до какого тура может дойти каждый из претендентов при наиболее благоприятном для него стечении обстоятельств. При этом для каждого участника в отдельности считается, что все недоговорные встречи, в том числе те, в которых он не участвует, закончатся так, как ему выгодно, а все состоявшиеся договорные встречи закончатся в соответствии с имеющимися договоренностями.

Требуется написать программу, которая для каждого из претендентов определяет максимальный номер тура, в котором он может участвовать.

Входные данные

В первой строке заданы три целых числа k (1 ≤ k ≤ 60), n (0 ≤ n ≤ 100 000) и m (1 ≤ m ≤ 100 000). В следующих n строках описаны n пар участников, которые договорились между собой о том, что первый из двух участников пары выиграет встречу, если она состоится. Гарантируется, что каждая пара участников присутствует во входных данных не более одного раза, при этом, если задана пара x y, то пары y x быть не может, кроме того, x ≠ y. В последней строке перечислены номера участников, желающих работать в Тапкодере, в порядке возрастания их номеров. Все номера претендентов на работу различны.

Выходные данные

Выходные данные должны содержать m целых чисел — максимальные номера туров, до которых могут дойти соответствующие претенденты на работу. Туры нумеруются от 1 до k.

Комментарии к примерам тестов.

1. У каждого из участников есть возможность выйти в финал, так как договорных матчей нет.

2. Если четвертый участник выиграет у третьего, то договорная встреча первого и третьего не состоится, что благоприятно для первого.

3. Первому участнику благоприятно во втором туре играть с третьим, а не с четвертым, в свою очередь, четвертый может выиграть у третьего и также выйти в финал.

Система оценки

Тесты к этой задаче состоят из четырех групп, баллы начисляются только при прохождении всех тестов группы и всех тестов предыдущих групп.

0. Тесты 1–10. k <= 5. Эта группа оценивается в 30 баллов.

1. Тесты 11–14. k <= 20. Эта группа оценивается в 20 баллов.

2. Тесты 15–18. k <= 30. Эта группа оценивается в 20 баллов.

3. Тесты 19–23. Дополнительные ограничения отсутствуют. Эта группа оценивается в 30 баллов.

Примеры
Входные данные
2 0 3
1 3 4
Выходные данные
2 2 2
Входные данные
3 1 1
3 1
1
Выходные данные
3
Входные данные
3 3 4
1 2
1 3
4 1
1 2 3 4
Выходные данные
3 1 2 3
Страница: << 42 43 44 45 46 47 48 >> Отображать по:
Выбрано
:
Отменить
|
Добавить в контест