Страница: << 73 74 75 76 77 78 79 >> Отображать по:
#1987
Игра
  
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes

Мальчик Вася играет в свою любимую RPG. Он нашел сундук с M ячейками, в каждой из которых лежит по одной бутылке с зельем лечения. У его героя на поясе есть N карманов, в каждом из которых также лежит по одной бутылке. Каждая бутылка восстанавливает фиксированное число очков здоровья.

Вася хочет заменить часть бутылок, находящихся в кармане на поясе, бутылками из сундука так, чтобы суммарное количество очков здоровья, восстанавливаемых бутылками, которые окажутся на поясе после этого, было максимальным. Ему доступна одна операция: поменять бутылку из указанного кармана пояса с бутылкой из указанной ячейки сундука.

Вам нужно указать последовательность операций, после которой суммарный запас очков здоровья у Васи на поясе будет максимальный.

Входные данные

Сначала вводятся N, M (1 ≤ N ≤ 1000, 1 ≤ M ≤ 1000). Далее идут N чисел, причём i-е равно количеству очков здоровья, восстанавливаемых бутылкой из i-го кармана пояса. Далее – M чисел, j-е из которых равно количеству очков здоровья, восстанавливаемых бутылкой из j-й ячейки сундука. Все очки – натуральные числа, не превосходящие 10000.

Выходные данные

Вначале выведите K – количество операций обмена. Оно не должно превышать 100000. Далее выведите K пар чисел, описывающих, какие бутылки нужно поменять: первое из чисел от 1 до N – задает номер кармана на поясе, второе – от 1 до M – номер ячейки в сундуке. Если существует более одного варианта, выведите любой.

Примечание
Возможный правильный ответ на первый пример
1
1 2
Возможный правильный ответ на второй пример
2
1 2
2 1
"Ответы", записанные ниже, являются служебной информацией для проверяющей системы.
Примеры
Входные данные
1 2
1
2 3
Выходные данные
3
Входные данные
2 2
3 1
4 5
Выходные данные
9
#1988
Строительство школы
  
Темы: [Цикл for]
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes

В деревне Интернетовка все дома расположены вдоль одной улицы по одну сторону от нее. По другую сторону от этой улицы пока ничего нет, но скоро все будет – школы, магазины, кинотеатры и т.д.

Для начала в этой деревне решили построить школу. Место для строительства школы решили выбрать так, чтобы суммарное расстояние, которое проезжают ученики от своих домов до школы, было минимально.

План деревни можно представить в виде прямой, в некоторых целочисленных точках которой находятся дома учеников. Школу также разрешается строить только в целочисленной точке этой прямой (в том числе разрешается строить школу в точке, где расположен один из домов – ведь школа будет расположена с другой стороны улицы).

Напишите программу, которая по известным координатам домов учеников поможет определить координаты места строительства школы.

Входные данные

Сначала вводится число N — количество учеников (0 < N < 100001). Далее идут в строго возрастающем порядке координаты домов учеников — целые числа, не превосходящие 2∙109 по модулю.

Выходные данные

Выведите одно целое число — координату точки, в которой лучше всего построить школу. Если ответов несколько, выведите любой из них.

Примеры
Входные данные
4
1 2 3 4
Выходные данные
3
Входные данные
3
-1 0 1
Выходные данные
0
#1989
Поклейка обоев
  
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes

Однажды майор Пронин затеял в квартире ремонт. В одной из стен на кухне по плану потребовалось последовательно проделать (N–1) прямоугольных вентиляционных отверстий с горизонтальными и вертикальными сторонами (0 < N < 101). Если оказывалось, что очередное отверстие пересекается с уже проделанными, то майор вырезал только нетронутую часть соответствующего прямоугольника.

Следующая стадия после ремонта – это поклейка обоев. В магазине напротив майор может заказать не более (2N–1)2 прямоугольных кусков обоев любых размеров c ненулевой площадью. Он хочет обклеить стену кусками обоев так, чтобы:

1. Вентиляционные отверстия не были заклеены даже частично.

2. Никакие два куска не пересекались (касаться сторонами они при этом могут).

На стене не осталось бы непокрытой области.

Рассмотрим декартову систему координат, оси которой параллельны сторонам отверстий и стены.

Входные данные

Сначала вводится число N (0 < N < 101), далее – описание N прямоугольников. Первый прямоугольник описывает положение стены в нашей системе координат, остальные (N–1) ― положения отверстий в порядке их появления. Стороны всех прямоугольников параллельны осям координат. Каждый прямоугольник задаётся координатами своих левого нижнего и правого верхнего углов: x1, y1, x2, y2. Координаты — целые числа, не превосходящие по модулю 31000, x1 < x2, y1 < y2.

Прямоугольники, обозначающие положение отверстий, могут пересекаться и касаться, поскольку это могло быть необходимо в ходе ремонта. Разумеется, все вентиляционные отверстия находятся в стене, то есть не выходят за границы первого прямоугольника.

Выходные данные

Вначале выведите количество кусков обоев K, которое нужно заказать в магазине (K должно быть не больше (2N–1)2). Далее выведите схему поклейки: K прямоугольников, обозначающих места расположения заказанных кусков. Для каждого прямоугольника нужно вывести координаты его левого нижнего и правого верхнего углов. Все координаты должны быть целыми числами. Гарантируется, что решение существует.

Если возможных способов несколько, выведите любой.

Примеры
Входные данные
2
-1 -1 2 2
0 0 1 1
Выходные данные
5
-1 -1 2 0
-1 0 0 2
0 1 1 2
1 0 2 1
1 1 2 2
#2529
Подарок
  
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
256 megabytes

Cреди всех прямоугольных параллелепипедов с натуральными длинами сторон и площадью поверхности не более \(n\) найти тот, объём которого максимален.

Начинающий программист Поликарп очень любит дарить подарки, особенно в коробках. Он давно заметил, что если коробка красиво оформлена, то радость от подарка возрастает многократно. Любой обёрточной бумаге он предпочитает клетчатую. В самом деле, после распаковки подарка на ней можно играть в крестики-нолики, морской бой, точки, а также решать задачи и писать программы.

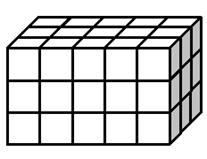
Поликарп очень аккуратен. Он упаковывает подарок в коробку, имеющую форму прямоугольного параллелепипеда, и оклеивает всю её поверхность клетчатой бумагой. При этом каждая грань коробки представляет собой прямоугольник, состоящий из целых клеток. На рисунке изображён пример такой упаковки подарка.

В настоящий момент Поликарп собирается поздравить свою подругу, недавно вернувшуюся с очередной олимпиады. Он хочет подарить ей подарок в большой и красивой коробке.

У Поликарпа в наличии есть лист клетчатой бумаги, состоящий из \(n\) клеток. Каким будет максимальный объём коробки, которую можно оклеить с использованием этого листа бумаги описанным выше способом? Поликарп может разрезать лист клетчатой бумаги по границам клеток произвольным образом и оклеивать коробку получившимися фигурами, поэтому форма листа не важна, а имеет значение только количество клеток на нём. Поликарп может использовать для оклеивания коробки не все клетки.

Напишите программу, которая по заданному количеству клеток \(n\) находит размеры коробки максимального возможного объема.

Входные данные

Входной файл содержит одно целое число \(n\) (\(6\le n\le10^{13}\)) — количество клеток на листе клетчатой бумаги.

Выходные данные

Выведите в первую строку выходного файла максимальный объём коробки, которую может подарить Поликарп. Объём следует выводить в «кубических клетках», то есть единицей измерения является куб со стороной, равной длине стороны клетки.

Во вторую строку выведите ширину, длину и высоту искомой коробки. Единица измерения — размер клетки. Числа разделяйте пробелами. Если решений несколько, то выведите любое из них.

Система оценивания

Решения, корректно работающие при \(n\le5\,000\), будут оцениваться из 30 баллов, а решения, корректно работающие при \(n\le10^8\), будут оцениваться из 70 баллов.

Примеры
Входные данные
6
Выходные данные
1
1 1 1
Входные данные
24
Выходные данные
8
2 2 2
#2530
ЮграНефтеТранс
  
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
256 megabytes

Задано множество из \(n\) станций и \(m\) трубопроводов, соединяющих некоторые пары станций. Требуется выбрать множество из \(k\) станций, чтобы один из двух концов каждого трубопровода лежал в выбранном множестве. Если построить граф, в котором станции будут служить вершинами, а трубопроводы — рёбрами, то искомое множество будет являться вершинным покрытием в этом графе.

Ханты-Мансийский автономный округ — Югра является важнейшим нефтяным регионом России. Добыча нефти составляет 267 млн т в год, её транспортировка осуществляется по трубопроводам, общая длина которых превышает длину экватора Земли.

Система транспортировки нефти представляет собой совокупность \(n\) распределительных станций и \(m\) трубопроводов. Каждый трубопровод соединяет две различные станции. Между любыми двумя станциями проложено не более одного трубопровода.

Эффективность работы станций существенно зависит от вязкости нефти. Поэтому компания «ЮграНефтеТранс», в ведении которой находится сеть трубопроводов, заказала инновационному исследовательскому предприятию разработку и изготовление новых сверхточных датчиков вязкости на основе самых современных технологий.

Изготовление датчиков — процесс трудоёмкий и дорогостоящий, поэтому было решено изготовить \(k\) датчиков (\(k\le40\)) и выбрать \(k\) различных станций, на которых датчики будут установлены. Необходимо осуществить выбор станций так, чтобы датчики контролировали все трубопроводы: для каждого трубопровода хотя бы один датчик должен быть установлен на станции, где начинается или заканчивается этот трубопровод.

Напишите программу, которая проверяет, существует ли требуемое расположение датчиков, и в случае положительного ответа находит это расположение.

Входные данные

В первой строке входного файла записаны три натуральных числа — \(n\), \(m\) и \(k\) (\(k\le n\le2000\), \(1\le m\le10^5\), \(1\le k\le40\)). Далее следуют \(m\) строк, каждая из которых описывает один трубопровод. Трубопровод задаётся двумя целыми числами — порядковыми номерами станций, которые он соединяет. Станции пронумерованы от 1 до \(n\). Гарантируется, что к любой станции подведён хотя бы один трубопровод и между любыми двумя станциями проложено не более одного трубопровода. Числа в каждой строке разделены пробелами.

Выходные данные

В первую строку выходного файла выведите слово «Yes», если требуемое расположение датчиков существует, в противном случае — слово «No». В случае положительного ответа выведите во вторую строку выходного файла \(k\) различных целых чисел — номера станций, на которых необходимо установить датчики. Номера можно выводить в любом порядке. Если существует несколько подходящих расположений датчиков, выведите любое из них. Разделяйте числа во второй строке пробелами.

Система оценивания

Решения, корректно работающие при \(n\le100\) и \(k\le10\), будут оцениваться из 60 баллов.

Примеры
Входные данные
9 12 4
1 2
2 3
1 4
4 5
1 6
6 7
1 8
8 9
2 5
4 7
6 9
8 3
Выходные данные
Yes
2 4 6 8
Входные данные
8 12 4
7 4
7 5
3 1
2 8
4 3
3 2
6 1
1 2
1 4
6 5
8 6
8 7
Выходные данные
No
Входные данные
4 3 1
3 1
3 2
3 4
Выходные данные
Yes
3
Страница: << 73 74 75 76 77 78 79 >> Отображать по:
Выбрано
:
Отменить
|
Добавить в контест