Темы --> Информатика --> Алгоритмы
    Задачи на моделирование(78 задач)
    Арифметические алгоритмы(240 задач)
    Алгоритмы поиска(155 задач)
    Алгоритмы сортировки(194 задач)
    Динамическое программирование(355 задач)
    Алгоритмы на графах(319 задач)
    Перебор(154 задач)
    Игры и выигрышные стратегии(33 задач)
    Вычислительная геометрия(216 задач)
    Эвристические методы(30 задач)
    Алгоритмы на строках(45 задач)
    Пересечение множеств(10 задач)
    Жадный алгоритм(71 задач)
    Теория расписаний(5 задач)
    Обработка текста(31 задач)
    Дата и время(14 задач)
---> 264 задач <---
Источники --> Командные олимпиады
    Школьная командная олимпиада ФМШ № 2007 г.Москвы(21 задач)
    Турнир Архимеда(52 задач)
    Кировские командные турниры(8 задач)
    Барнаульские командные турниры(10 задач)
    Московская командная олимпиада(246 задач)
    Командные чемпионаты школьников Санкт-Петербурга по программированию(167 задач)
    ВКОШП(180 задач)
Страница: << 16 17 18 19 20 21 22 >> Отображать по:
#778
Крестики
  
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes

Требуется расставить в некоторые клетки таблицы 3 x 3 крестики так, чтобы в каждой строке и в каждом столбце было заданное количество крестиков.

Входные данные

Вводятся 6 чисел (от 0 до 3) – требуемое количество крестиков в первом, втором, третьем столбце, в первой, второй, третьей строке.

Выходные данные

Требуется выдать количество возможных таблиц или 0, если таких таблиц нет.

Примеры
Входные данные
1 1 1 1 1 1
Выходные данные
6
Входные данные
3 3 3 1 1 1
Выходные данные
0
#787
Будильники
  
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes

Будильник в сотовом телефоне можно настроить так, чтобы он звонил каждый день в одно и то же время, либо в указанное время в определенный день недели. Независимо можно настроить несколько будильников.

По информации о будильниках и текущему времени и дню недели определите, когда прозвонит очередной будильник.

Входные данные

В первой строке вводятся три числа, задающие текущее время: день недели (от 1 до 7), часы и минуты.

Во второй строке вводится одно натуральное число N, не превосходящее 100 – количество будильников.

В следующих N строках вводятся описания N будильников. Описание каждого будильника состоит из трех чисел: дня недели (число от 1 до 7 для понедельника,  …, воскресенья, соответственно, 0 – если будильник должен звонить каждый день), часов (от 0 до 23), минут (от 0 до 59).

Выходные данные

Выведите  через пробел три числа, задающие день недели, часы и минуты, когда прозвонит ближайший будильник.

Комментарий. Во втором примере третий будильник будет звенеть в начальный момент времени.
Примеры
Входные данные
2 10 20
2
1 23 15
0 10 10
Выходные данные
3 10 10
Входные данные
7 1 1
3
7 0 59
7 23 59
7 1 1
Выходные данные
7 1 1
#854
Складирование ноутбуков
  
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
64 megabytes

На склад, который имеет форму прямоугольного параллелепипеда, привезли ноутбуки, упакованные в коробки. Каждая коробка также имеет форму прямоугольного параллелепипеда.

По правилам хранения коробки с ноутбуками должны быть размещены на складе с выполнением следующих двух условий:

Стороны коробок должны быть параллельны сторонам склада

Коробку при помещении на склад разрешается расположить где угодно (с выполнением предыдущего условия), в том числе на другой коробке, но все коробки должны быть ориентированы одинаково (т.е. нельзя одну коробку расположить «стоя», а другую – «лежа»)

Напишите программу, которая по размерам склада и размерам коробки с ноутбуком определит максимальное количество ноутбуков, которое может быть размещено на складе.

Входные данные

Вводится шесть натуральных чисел. Первые три задают длину, высоту и ширину склада. Следующие три задают соответственно длину, высоту и ширину коробки с ноутбуком. Каждое из чисел не превышает 1000.

Выходные данные

Выведите одно число — максимальное количество ноутбуков, которое может быть размещено на складе.

Примеры

Входные данные

Выходные данные

100 200 300

1 2 3

1000000

100 200 300

3 2 1

1000000

100 100 1

2 2 2

0

7 7 7

3 3 3

8
#855
Сортировка вагонов
  
Необходимо упорядочить числа с помощью стека.

К тупику со стороны пути 1 (см. рисунок) подъехал поезд. Разрешается отцепить от поезда один или сразу несколько первых вагонов и завезти их в тупик (при желании, можно даже завезти в тупик сразу весь поезд). После этого часть из этих вагонов вывезти в сторону пути 2. После этого можно завезти в тупик еще несколько вагонов и снова часть оказавшихся вагонов вывезти в сторону пути 2. И так далее (так, что каждый вагон может лишь один раз заехать с пути 1 в тупик, а затем один раз выехать из тупика на путь 2). Заезжать в тупик с пути 2 или выезжать из тупика на путь 1 запрещается. Нельзя с пути 1 попасть на путь 2, не заезжая в тупик.

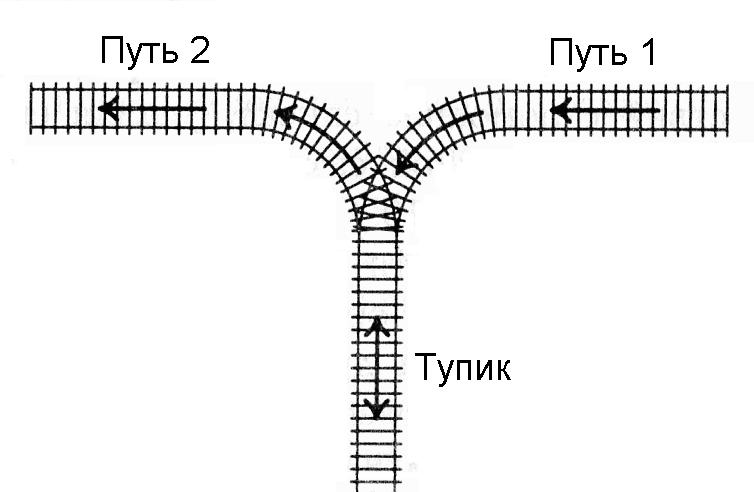
Известно, в каком порядке изначально идут вагоны поезда. Требуется с помощью указанных операций сделать так, чтобы вагоны поезда шли по порядку (сначала первый, потом второй и т.д., считая от головы поезда, едущего по пути 2 в сторону от тупика).

Входные данные

Вводится число N — количество вагонов в поезде (1≤N≤2000). Дальше идут номера вагонов в порядке от головы поезда, едущего по пути 1 в сторону тупика. Вагоны пронумерованы натуральными числами от 1 до N, каждое из которых встречается ровно один раз.

Выходные данные

Если сделать так, чтобы вагоны шли в порядке от 1 до N, считая от головы поезда, когда поезд поедет по пути 2 из тупика, можно, выведите действия, которые нужно проделать с поездом. Каждое действие описывается двумя числами: типом и количеством вагонов:

  • если нужно завезти с пути 1 в тупик K вагонов, должно быть выведено сначала число 1, а затем — число K (K≥1),
  • если нужно вывезти из тупика на путь 2 K вагонов, должно быть выведено сначала число 2, а затем — число K (K≥1).

Если возможно несколько последовательностей действий, приводящих к нужному результату, выведите любую из них.

Если выстроить вагоны по порядку невозможно, выведите одно число 0.

Примеры

Входные данные

Выходные данные

3

3 2 1

1 3

2 3

4

4 1 3 2

1 2

2 1

1 2

2 3

3

2 3 1

0
#856
Остаток от деления на цифру
  
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
64 megabytes

Напишите программу, вычисляющую остаток от деления заданного «длинного» числа на заданную цифру.

Входные данные

В первой строке задана цифра K (1≤K≤9). Во второй строке задано натуральное число N, состоящее из не более чем 100000 цифр.

Выходные данные

Выведите остаток от деления N на K.

Примеры

Входные данные

Выходные данные

5

123456789

4

1

123

0
Страница: << 16 17 18 19 20 21 22 >> Отображать по:
Выбрано
:
Отменить
|
Добавить в контест