В городском зоопарке содержатся животные n разных видов. Для участия в международной выставке «Три твари» зоопарк должен представить трех животных различных видов. Теперь служителей зоопарка интересует, сколькими способами можно выбрать трех животных для участия в выставке.

Например, если в зоопарке два медведя, тигр, лев и пингвин, то есть семь способов выбрать трех животных:

1) первый медведь, тигр и лев;

2) первый медведь, тигр и пингвин;

3) первый медведь, лев и пингвин;

4) второй медведь, тигр и лев;

5) второй медведь, тигр и пингвин;

6) второй медведь, лев и пингвин;

7) тигр, лев и пингвин.

Вася идет из школы домой вдоль проспекта, по которому ходят трамваи. Мама считает, что ему после школы полезно дышать свежим воздухом, поэтому настаивает, чтобы не менее K метров он прошел пешком. Вася при этом хочет попасть домой как можно быстрее (обязательно выполнив требование мамы).

Вдоль проспекта расположено N трамвайных остановок, которые находятся в точках a₁, a₂, ..., a_N (все координаты задаются в метрах). Школа находится около 1-й остановки, а дом — около остановки номер N. Мальчик идет пешком со скоростью v метров в минуту. Трамвай едет со скоростью w метров в минуту (временем стоянки трамвая на остановках пренебрежем). В нулевой момент времени и далее с интервалом T минут от первой остановки в сторону Васиного дома отправляются трамваи. Вася выходит из школы также в момент времени 0. Сесть в трамвай и выйти из него можно только на остановке. При этом, если Вася приходит на остановку раньше трамвая, на который хочет сесть, то ему придется подождать, пока тот не подъедет. Вася идет пешком и едет на трамвае только в направлении от школы к дому.

Напишите программу, которая определит, когда Вася сможет оказаться дома.

Каждый раз, когда в мире происходит значимое событие, наша реальность разветвляется на несколько — в зависимости от исхода этого события. После этого существует уже не только наша основная реальность, но и ответвившиеся от неё в моменты появления разных исходов.

Однажды один архимаг решил сделать мир лучше. Такая грандиозная задача не под силу одному архимагу, поэтому он решил найти самого себя ещё в K реальностях и выполнить эту задачу вместе. Проведённое теоретическое исследование показало, что, кроме реальности, в которой находится именно он, существует ещё N - 1 реальностей. Для удобства они были занумерованы числами от 1 до N, при этом его собственная реальность имеет номер 1, а посетить ему необходимо реальности с номерами 2, 3, ..., K + 1.

Как уже говорилось, каждая реальность когда-то ответвилась от некоторой другой, за исключением одной Начальной реальности, которая существовала всегда (её номер может оказаться каким угодно; считается, что она появилась в момент времени 0). Исследование показало, что реальность с номером i ответвилась от реальности с номером P_i в момент времени T_i. Из каждой реальности с номером i архимаг может переместиться

• в любую ответвившуюся от неё, то есть в любую j, такую что P_j = i;
• в P_i, если i — не Начальная реальность.

Требуется найти минимальное количество энергии, которое потребуется архимагу, чтобы, начав в реальности с номером 1, посетить все реальности с номерами от 2 до K + 1 (в любом порядке) и затем вновь вернуться в 1. Любую реальность при этом разрешается посещать сколько угодно раз.

Антон - большой любитель компьютерных игр. Совсем недавно вышла новая игра Heroes of Keyboard and Mouse, и он, конечно же, сразу ее купил и установил на свой компьютер. Эта игра относится к жанру квестов, и поэтому ее прохождение сводится к последовательному выполнению ряда заданий (квестов).

Один из квестов, над которым Антон бьется уже не первый день состоит в том, что требуется открыть замок. Замок состоит из \(n\) шестеренок, стоящих в ряд - \(i\)-ая из шестеренок имеет \(s_i\) зубцов, на каждом из которых написано число от \(0\) до \(s_i - 1\). Первая шестеренка зацеплена только со второй, вторая зацеплена с первой и третьей, третья - со второй и четвертой, ..., \((n-1)\)-ая - с \((n-2)\)-ой и \(n\)-ой, \(n\)-ая только с \((n-1)\)-ой.

На замке имеется \(n\) окошечек и \(n\) ручек - в \(i\)-ое окошко можно видеть число, написанное на одном из зубцов \(i\)-ой шестеренки, а с помощью \(i\)-ой ручки можно поворачивать \(i\)-ую шестеренку. При этом числа на шестеренках расположены таким образом, что если до поворота \(i\)-ой из них по часовой стрелке на одно деление в \(i\)-ом окошке было видно число \(x\), то после поворота будет видно число \((x+1) \bmod s_i\). Аналогично, после поворота против часовой стрелки на одно деление вместо числа \(x\) будет видно число \((x-1+s_i) \bmod s_i\). Разумеется, если шестеренку повернуть по часовой стрелке, то непосредственно зацепленные с ней шестеренки повернутся против часовой стрелки, и наоборот, если шестеренку повернуть против часовой стрелки, то они повернутся по часовой стрелке. 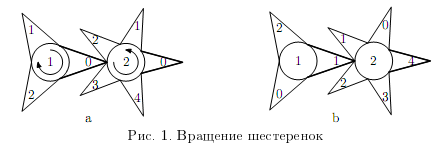Слева на рис.1 показано положение шестеренок до поворота первой из них по часовой стрелке, справа на рис. 1 показано положение шестеренок после указанного поворота. Более толстыми линиями нарисован тот зубец шестеренки, число на котором видно в соответствующее окошко замка.

Изначально замок находится в состоянии, в котором в \(i\)-ое окошко видно число \(a_i\). Для того, чтобы его открыть, необходимо перевести его в состояние, в котором в \(i\)-ое окошко видно число \(b_i\).

С помощью \(i\)-ой ручки можно поворачивать \(i\)-ую шестеренку. Разумеется, если повернуть \(i\)-ую шестеренку, то придут в движение и все шестеренки, с которыми она соединена - напрямую или через другие шестеренки. Поворот любой шестеренки на одно деление занимает одну секунду. Кроме этого, если \(i\)-ая шестеренка находится в таком состоянии, что в \(i\)-ое окошко видно число \(b_i\) (то есть, она находится в положении, соответствующем требуемому состоянию замка), то ее можно вдавить, нажав на ее ручку. В результате этого \(i\)-ая шестеренка перестает быть соединенной с \((i-1)\)-ой и \((i+1)\)-ой (если, конечно, они существуют). Вдавленная шестеренка остается в таком состоянии навсегда. 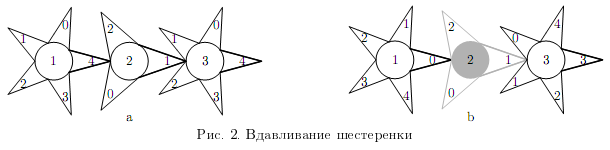На то, чтобы нажать на ручку и вдавить шестеренку требуется \(k\) секунд. На рис. 2 слева показано положение шестеренок до вдавливания второй из них, а справа - после вдавливания и после поворота первой по часовой стрелке, а третьей - против. Отметим, что после вдавливания второй шестеренки первая и третья вращаются независимо друг от друга.

Для того, чтобы выполнить квест, Антону необходимо открыть замок как можно быстрее. Напишите программу, которая по описанию замка, его начального состояния и требуемого состояния, вычислит минимальное время, за которое Антон может открыть замок.