На днях Алиса делала уборку в своей комнате и нашла дневник, который вела в начальной школе. Там она с удивлением обнаружила запись о том насколько ее поразило то, что \(2 + 2 = 2 \cdot 2\). Невероятно, умножение и сложение дают один и тот же результат!

Эта запись натолкнула Алису на следующую задачу: пусть целые заданы числа \(a\) и \(b\). Сколько различных значений в наборе чисел

Деление происходит без округления, результат деления может не быть целым числом. Если какое-либо выражение из этого набора некорректно, то Алиса его не рассматривает. Некорректными считаются деление на ноль и возведение нуля в неположительную степень.

На планете Шелезяка катастрофа — запасы смазки подходят в концу. В связи с этим правительство решило организовать всепланетное соревнование, главный приз в котором — вагон смазочных материалов.

Соревнование проводится в несколько этапов, каждый из которых поделен на множество раундов. В каждом раунде принимают участие два игрока. Жюри предоставляет им большое целое число \(n\). Затем игроки делают ходы по очереди. Первый ход первого игрока заключается в том, что игрок выписывает на специальном поле цифру, причем первым ходом запрещается выписывать ноль. В дальнейшем ход игрока заключается в том, что он приписывает справа к уже написанному числу произвольную цифру. Выигрывает тот, после чьего хода выписанное число больше или равно \(n\).

Знаменитый ученый-робот «ЩК-33» считает, что результат игры легко предсказуем. Для доказательства он решил предоставить программу, которая определяет, кто выигрывает, если оба игрока действуют по оптимальной стратегии. К сожалению, из-за недостатка смазки, его манипуляторы вышли из строя, поэтому он просит вас о помощи.

Джон работает на огромной парковке. Парковка представляется собой прямоугольное поле \(n \times m\), разбитое на \(n \times m\) квадратных позиций размера \(1 \times 1\). Одну из угловых позиций занимает выезд с парковки.

Машин на парковке много и вывести машину не так уж просто. Единственное, что Джон может сделать — это переместить один из автомобилей на соседнюю позицию, если она свободна. Соседними считаются позиции, имеющие общую сторону. Однако задача усложняется наличием на парковке столбов. На позиции, где стоят столбы, нельзя поставить машину. Парковка вся занята машинами и столбами и единственное свободное место — выезд с парковки. Задача Джона — вывести с парковки один из автомобилей. Помогите ему узнать, какое минимальное число действий ему придется совершить.

Директор школы «Лицей Программистов» города Линейска сумел привить ученикам этой школы хорошую дисциплину, но, несмотря на это, многие ученики продолжают опаздывать на уроки.

В Линейске есть всего одна главная улица, на которой расположен и сам лицей, и живут все его ученики. Дисциплинированные школьники выходят из своих домов в одно и то же время. Но, к сожалению, все они живут на разном расстоянии от школы и добираются с разной, но постоянной скоростью (среди учеников есть как весьма неторопливые, так и будущая чемпионка мира по бегу на 100 метров Маша Гайка).

Для улучшения ситуации с опозданиями школа купила один веломобиль, который взялся водить сторож школы. Веломобиль способен помимо водителя перевозить одного школьника. Веломобиль перемещается с постоянной скоростью \(v\).

Ночь веломобиль проводит в школьном гараже, а утром, ровно в тот момент, когда все ученики выходят из своих домов, отправляется им навстречу, чтобы подвезти какого-нибудь школьника. Конечно же, ему приходится подвозить школьника прямо до ворот школы, потому как никто не хочет быть высаженным посреди пути. После того, как веломобиль помог одному ученику быстрее добраться в учебное заведение, он снова может ехать навстречу следующему опаздывающему человеку.

Директор хочет начинать занятия как можно раньше, но для этого нужно, чтобы все ученики добрались до лицея. Он поручил вам помочь составить план, по которому должен действовать водитель веломобиля, чтобы время прибытия последнего школьника в школу было минимальным.

Новый мэр крупного города Флатбурга Иван Котянин начал свою работу с решения проблем с пробками в городе. Как и в любом крупном городе, во Флатбурге есть кольцевая автодорога. Во Флатбурге она представляет собой монотонный многоугольник. Монотонным называется многоугольник, с которым каждая прямая, проходящая строго с севера на юг, имеет не более двух общих точек.

После совещания с правительством города было принято решение построить новую магистраль — скоростной диаметр, который вел бы строго с севера на юг и соединял две точки кольцевой автодороги.

Помимо борьбы с пробками решено было обновить рекорд по протяженности самой длинной магистрали, проложенной с севера на юг. Для того чтобы обновить рекорд необходимо построить магистраль длиной хотя бы \(d\) километров, а поскольку лишних денег в бюджете Флатбурга не так уж и много, решено было построить дорогу длиной ровно \(d\).

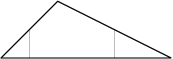
Министр транспорта Флатбурга решил предоставить мэру все варианты строительства новой дороги. Для начала он решил подсчитать, сколько существует способов построить магистраль. Помогите министру.