Страница: << 16 17 18 19 20 21 22 Отображать по:

#111288

Телефонный номер

Темы: [Динамическое программирование]

Источники: [ Командные олимпиады, ВКОШП, 2011, Задача C ]

Недавно Васе продиктовали номер телефона. Он записал его, разделив числа дефисами, но потом начал сомневаться, не ошибся ли он в записи номера. Ведь бывают различные телефонные номера, которые произносятся одинаково. Например, все четыре номера «3000-100-1», «3000-101», «3100-1», «3101» читаются как «три тысячи сто один». Теперь он хочет выяснить, какие номера произносятся также, как и записанный им номер.

Вася считает, что при произношении телефонного номера не употребляются числа, состоящие более чем из девяти цифр. Напомним, как произносятся числа от $1$ до $999\,999\,999$.

Если число больше или равно $1\,000\,000$, то сначала произносится число миллионов в мужском роде, затем слово «миллион», «миллиона» или «миллионов», по следующим правилам. Если число миллионов, взятое по модулю 100, не равно 11 и дает остаток 1 по модулю 10, то произносится слово «миллион». Если число миллионов, взятое по модулю 100, не равно 12, 13 или 14 и дает остаток 2, 3 или 4 по модулю 10, то произносится слово «миллиона». Иначе произносится слово «миллионов».

Если число по модулю $1\,000\,000$ больше или равно $1\,000$, то затем произносится число тысяч в женском роде, затем слово «тысяча», «тысячи» или «тысяч», по следующим правилам. Если число тысяч, взятое по модулю 100, не равно 11 и дает остаток 1 по модулю 10, то произносится слово «тысяча». Если число тысяч, взятое по модулю 100, не равно 12, 13 или 14 и дает остаток 2, 3 или 4 по модулю 10, то произносится слово «тысячи». Иначе произносится слово «тысяч».

Затем, если число по модулю $1\,000$ отлично от нуля, в мужском роде произносится число единиц.

Например, число $978\,121\,014$ произносится как «девятьсот семьдесят восемь миллионов сто двадцать одна тысяча четырнадцать», а число $1\,000\,142$ как «один миллион сто сорок два». Заметим, что перед словом «миллион» нельзя опускать слово «один», перед словом «тысяча» слово «одна», а числа от $11$ до $19$ произносятся одним словом.

Помогите Васе найти все телефонные номера, которые произносятся так же, как тот, который он записал.

Входные данные

На входе единственная строка, содержащая номер записанного Васей телефона. Номер телефона --- это целые числа, разделенные символом «-» (ASCII код 39). Каждое число в записи положительно, содержит не более девяти цифр и не содержит ведущих нулей. Гарантируется, что в записанном Васей номере встречается не больше 50 цифр.

Выходные данные

В первой строке выведите количество телефонных номеров, которые читаются так же, как и записанный Васей номер. В следующих строках выведите эти номера телефонов. Каждый номер должен находиться в отдельной строке. Каждый номер должен состоять из чисел от 1 до $999\,999\,999$, разделенных дефисами.

Порядок телефонов в ответе не важен. Гарантируется, что количество номеров в ответе не превышает $100\,000$. Учтите, что в ответе могут встречаться и номера, составленные более чем из 50 цифр.

Примеры тестов

Входные данные

3000-101

Выходные данные

#111295

Поезда

Темы: [Генерация по номеру] [Динамическое программирование]

Источники: [ Командные олимпиады, ВКОШП, 2011, Задача J ]

Маленький Вася очень любит поезда. На день рождения ему подарили игрушечную железную дорогу. В комплект к железной дороге входит поезд, состоящий из $n$ вагонов, пронумерованных числами от 1 до $n$.

Любимым занятием Васи стала сортировка поездов с использованием специального сортировочного тупика.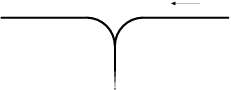 $\text{[math]}$

Справа к тупику подъезжает поезд, составленный из всех $n$ вагонов. Затем вагоны по одному загоняются в сортировочный тупик и выгоняются из него налево. Васе нравится, если ему удается отсортировать поезд с помощью сортировочного тупика — добиться того, чтобы слева от тупика вагоны были расположены по порядку от 1 до $n$.

Например, пусть в исходном поезде 4 вагона, которые следуют в порядке 3, 1, 2, 4. Его можно отсортировать следующим образом. Загоняем вагон 3 в тупик. Загоняем вагон 1 в тупик. Выгоняем вагон 1 из тупика. Загоняем вагон 2 в тупик. Выгоняем вагон 2 из тупика. Выгоняем вагон 3 из тупика. Загоняем вагон 4 в тупик. Выгоняем вагон 4 из тупика.

Не все поезда можно отсортировать таким образом. Например, поезд из 3 вагонов, следующих в порядке 2, 3, 1, отсортировать нельзя.

Вася выписал на листке в лексикографическом порядке все поезда длины $n$, которые можно отсортировать с помощью тупика. Поезд $(a_1, a_2, \ldots, a_n)$ идет раньше поезда $(b_1, b_2, \ldots, b_n)$ в лексикографическом порядке, если существует такое $i$ ($1 \le i \le n$), что для всех $j < i$ выполняется $a_j = b_j$, а $a_i < b_i$. Например, все поезда из трех вагонов, которые можно отсортировать с помощью тупика, в лексикографическом порядке выписываются следующим образом: $(1, 2, 3)$, $(1, 3, 2)$, $(2, 1, 3)$, $(3, 1, 2$), $(3, 2, 1)$.

Вася потерял свой листок, и его интересует вопрос: какой поезд был выписан на его листке под номером $k$. Помогите ему выяснить это.

Входные данные

Входной файл содержит два целых числа — $n$ и $k$ ($1 \le n \le 30$, $1 \le k \le 10^{18}$).

Выходные данные

Выведите в выходной файл $n$ целых чисел: $k$-й в лексикографическом порядке поезд из $n$ вагонов, который можно отсортировать с помощью тупика.

Если с помощью тупика можно отсортировать менее $k$ поездов из $n$ вагонов, выведите $-1$.

Примеры тестов

Входные данные

4 1

Выходные данные

1 2 3 4

Входные данные

4 3

Выходные данные

1 3 2 4

Входные данные

4 15

Выходные данные

-1

#111824

Спасти котенка

Темы: [Комбинаторика] [Динамическое программирование]

Источники: [ Командные олимпиады, ВКОШП, 2012, Задача F ]

Артур принимает участие в телешоу, в котором участникам необходимо выполнять различные интеллектуальные и физические задания, чтобы зарабатывать очки. В одном из таких заданий Артуру необходимо спасти маленького котенка.

Поле для выполнения задания представляет собой прямоугольник размером $n \times m$ метров, разбитый на квадраты единичной площади. В одном из квадратов исходно находится Артур, в некотором другом квадрате находится котенок. Кроме того, один из квадратов содержит лифт, встав на который вместе с котенком, Артур успешно выполняет задание.

За один шаг Артур может перемещаться на любой квадрат, имеющий общую сторону с тем, на котором он стоит. После этого квадрат, на котором перед этим шагом стоял Артур, исчезает и больше на него вставать нельзя. Таким образом исчезают в том числе и квадрат, на котором исходно стоял Артур, и квадрат с котенком. Цель Артура - дойти до котенка, взять его и затем дойти до лифта. При этом очки за выполнение задания, зависят от числа шагов, которое сделает Артур, поэтому ему необходимо сделать минимальное число шагов.

Выяснив, сколько шагов ему придется сделать, Артур заинтересовался, сколько существует различных способов дойти до котенка, а затем с ним до лифта, сделав в сумме минимальное число шагов. Помогите ему это выяснить. Это число может быть довольно большим, поэтому Артур просит найти его по модулю $10^9+7$.

Формат входного файла

Первая строка входного файла содержит два натуральных числа $n$ и $m$ - размеры поля для выполнения задания ($2 \le n, m \le 100$).

Вторая строка содержит два целых числа $x_A$ и $y_A$ - координаты квадрата, на котором исходно находится Артур ($1 \le x_A \le n$, $1 \le y_A \le m$). Третья строка содержит два целых числа $x_K$ и $y_K$ - координаты квадрата, на котором сидит котенок ($1 \le x_K \le n$, $1 \le y_K \le m$). Четвертая строка содержит два целых числа $x_E$ и $y_E$ - координаты квадрата, на котором находится лифт ($1 \le x_E \le n$, $1 \le y_E \le m$). Эти три квадрата попарно различны.

Формат выходного файла

В единственной строке выходного файла выведите одно число - число способов дойти до котенка и затем до лифта, не наступая на один квадрат два раза, совершив при этом минимальное количество шагов. Число необходимо вывести по модулю $10^9+7$.

Пояснения к примеру

$\text{[math]}$

Два способа для поля, приведенного в примере.

Примеры

Входные данные

Выходные данные

#111828

Швабра

Темы: [Вычислительная геометрия]

Источники: [ Командные олимпиады, ВКОШП, 2012, Задача J ]

Первокурсник Рома приехал в общежитие и, удивившись беспорядку в комнате и толстому слою пыли на полу, начал наводить порядок. Первым делом он решил вымыть пол. Для этого Рома в магазине приобрел инновационную швабру.

Изначально моющая часть швабры имела идеальную прямоугольную форму, но в процессе перевозки из магазина в общежитие у нее отломился один из углов. Таким образом, теперь она представляет собой многоугольник, граница которого состоит из двух соседних сторон прямоугольника, фрагментов двух оставшихся сторон и ломаной, соединяющей концы этих фрагментов.

$\text{[math]}$

Рома живет в большой прямоугольной комнате. Рома провел сломанной шваброй от одной стороны комнаты до другой, не отрывая ее от стены, так что в результате отломанный угол швабры оказался в углу комнаты. При этом часть соответствующей прямоугольной полосы пола в углу осталась невымытой.

$\text{[math]}$

Рома считает, что все точки, в которых в какой-то момент находилась моющая часть швабры оказались вымыты. Теперь он решил выяснить, какая часть этой полосы осталась грязной.

$\text{[math]}$

Помогите ему вычислить площадь этой части. Можете считать, что размер комнаты, в которой живет Рома, существенно больше размеров моющей части швабры.

Формат входного файла

Первая строка входного файла содержит два целых числа $w$ и $h$ - размеры моющей части швабры до повреждения ($2 \le w, h \le 10^5$).

Вторая строка содержит целое число $n$ - число вершин ломаной, соединяющей соседние стороны швабры ($2 \le n \le 10^5$). В $i$-й из следующих $n$ строк заданы два целых числа $x_i$ и $y_i$ ($1 \le x_i < w$, $1 \le y_i < h$, за исключением $y_1 = h$, $x_n = w$) - координаты $i$-й вершины ломаной. Ломаная не имеет самопересечений и самокасаний.

Координаты введены таким образом, что стена, вдоль которой Рома провел шваброй, соответствует прямой $y=h$.

Формат выходного файла

В выходной файл выведите площадь невымытой части пола с абсолютной или относительной погрешностью не более $10^{-6}$. Это значит, что если правильный ответ $a$, а вы вывели $p$, то ваш ответ будет засчитан как правильный, если $\frac{|a-p|}{\max(|a|, 1)}\le 10^{-6}$.

Примеры

Входные данные

Выходные данные

18.0

#111975

Город Че

Темы: ["Два указателя"]

Источники: [ Командные олимпиады, ВКОШП, 2013, Задача B ]

В центре города Че есть пешеходная улица - одно из самых популярных мест для прогулок жителей города. По этой улице очень приятно гулять, ведь вдоль улицы расположено $n$ забавных памятников.

Девочке Маше из города Че нравятся два мальчика из ее школы, и она никак не может сделать выбор между ними. Чтобы принять окончательное решение, она решила назначить обоим мальчикам свидание в одно и то же время. Маша хочет выбрать два памятника на пешеходной улице, около которых мальчики будут ее ждать. При этом она хочет выбрать такие памятники, чтобы мальчики не увидели друг друга. Маша знает, что из-за тумана мальчики увидят друг друга только в том случае, если они будут на расстоянии не более $r$ метров.

Маше заинтересовалась, а сколько способов есть выбрать два различных памятника для организации свиданий.

Формат входного файла

В первой строке входного файла находятся два целых числа $n$ и $r$ ($2 \le n \le 300\,000$, $1 \le r \le 10^9$) - количество памятников и максимальное расстояние, на котором мальчики могут увидеть друг друга.

Во второй строке задано $n$ положительных чисел $d_1, \ldots, d_n$, где $d_i$ - расстояние от $i$-го памятника до начала улицы. Все памятники находятся на разном расстоянии от начала улицы. Памятники приведены в порядке возрастания расстояния от начала улицы ($1 \le d_1 < d_2 < \ldots < d_n \le 10^9$).

Формат выходного файла

Выведите одно число - число способов выбрать два памятника для организации свиданий.

Пояснения к примеру

В приведенном примере Маша может выбрать памятники под номерами 1 и 4 или памятники 2 и 4.

Примеры

Входные данные

4 4
1 3 5 8

Выходные данные

Страница: << 16 17 18 19 20 21 22 Отображать по:

Выбрано

Отменить

Добавить в контест