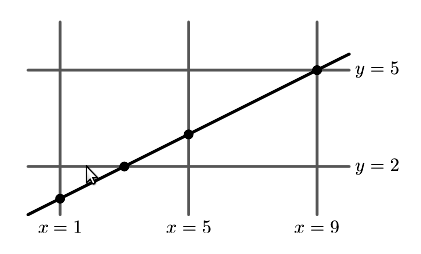
Вы отвечаете за электрическую сеть для некоторого соревнования по программированию и вам надо подключить много компьютеров к источнику питания. К сожалению, есть два стандарта для вилок и розеток: A и B. Эти стандарты несовместимы между собой, так что вилка стандарта A может быть включена только в розетку стандарта А, и вилка стандарта B может быть включена только в розетку стандарта B.
В зале соревнований есть только одна розетка стандарта A. Каждый компьютер, который будет использован в соревновании, имеет вилку стандарта A. Таким образом, только один компьютер может быть подключен напрямую к главной розетке. Но вы можете использовать разветвители питания двух типов.
- Разветвитель первого типа имеет одну вилку стандарта A и несколько розеток стандарта B.
- Разветвитель второго типа имеет одну вилку стандарта B и несколько розеток стандарта A.
Все разветвители питания очень мощные и могут выдержать любую нагрузку. Так что вы можете создать электрическую сеть, подключив один разветвитель первого типа к главной розетке, затем несколько разветвителей второго типа к этому разветвителю, и так далее. В конце вы получите несколько розеток, к которым вы можете присоединить компьютеры.
Вы должны найти максимальное число компьютеров, которые могут быть подключены к сети, используя доступные разветвители.
Возможное решение для первого примера: 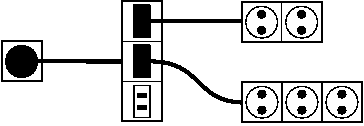 Возможное решение для второго примера:
Возможное решение для второго примера: 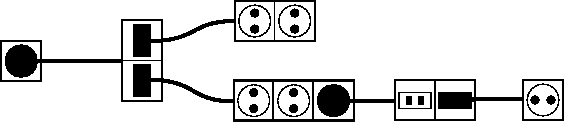
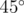 . Возможна постройка промежуточного подземного вестибюля и двух эскалаторов. Вам даны
. Возможна постройка промежуточного подземного вестибюля и двух эскалаторов. Вам даны  Возможное решение для второго примера:
Возможное решение для второго примера: