В сказочной стране, столицей которой является Изумрудный Город, всего N городов. Некоторые города соединены дорогой, целиком вымощеной желтым кирпичем. Элли нужно добраться из города на границе в Изумрудный Город и затем вернуться обратно. Чтобы не было скучно, ей хочется добираться туда и обратно разным маршрутом (а именно так, чтобы ни одна из дорог не была и на маршруте туда и на маршруте обратно). Поскольку зря тратить время она не собирается, то для каждого пути она хочет выбрать самый короткий вариант.
Напишите программу, которая поможет Элли определить, возможно ли такое путешествие, и если оно возможно, то разработает для нее маршрут.
Все города пронумерованы натуральными числами от 1 до N, город на границе имеет номер K, Изумрудный Город имеет номер N.
Выходные данные
В первой строке выведите -1, если желание Элли неосуществимо. В противном случае в первой строке выведите два числа: длину пути туда и длину пути обратно, а в следующих двух строках: номера городов на пути туда и на пути обратно в том порядке, в котором она будет их проходить.
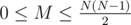 ), где
), где